20 Optimum Product Mix

The Theory

In a manufacturing setting, constraints on production capacity, which occur when a resource or resources are limited, can make a firm unable to produce all the goods that their customers demand.

When a firm under constraints manufactures multiple products, the product mix, or how much of each of a firm’s products is sold relative to each other, can affect how much profit the firm earns. The firm may be tempted to maximize production of the product that earns the highest profit per unit, but they should also take into account how each product uses the firm’s constrained resources.

When the firm faces only one constraint, they will maximize profits if they prioritize production of products that maximize throughput margin (revenues minus direct materials cost) per unit of constrained capacity.

When the firm faces multiple constraints, they can use linear programming, a mathematical model for maximizing an outcome, to determine the optimum mix of products that will provide the most throughput margin given limited production resources.

The Method

The procedure you should use to determine the optimum product mix depends on how many constraints the firm has.

Optimum Mix Under One Constraint

If only one constraint exists, the first step is to rank the products from highest to lowest in order of throughput margin per unit of constrained resource. You’d first find the throughput margin per unit, then divide by the amount of the constrained resource each unit uses to find the throughput margin per unit of constrained resource. Use this amount to rank the products from highest to lowest.

Next, determine the units of each product in the optimum product mix. Starting with the highest-ranked product, calculate the resource needed to meet its demand. Subtract that amount from the total available resource and repeat for the next product. When the remaining resource is insufficient to meet full demand, calculate how many units of that product can be made with the amount of resource that is left. Any remaining products should not be produced. Express the results of this process in units.

Optimum Mix Under Multiple Constraints

If multiple constraints exist, use linear programming.

First, state the objective function. Your objective is to maximize throughput margin, so represent throughput margin mathematically.

Next, set up inequalities for each of the constraints. Each constrained resource has a limited available quantity, so total production must not exceed this amount. Represent these inequalities mathematically.

Next (optionally), graph the constraints, if it will help you understand the problem better.

Next, find the corner points of the area of feasible solutions by finding the points where each constraint line crosses the x- and y-axis and solving the equations for the constraint lines simultaneously where they cross each other.

Finally, plug the corner points into the objective function to determine which mix earns the greatest throughput margin.

Illustrative Example

Faerie Manufacturing produces two products using technicians who work in three processes—molding, finishing, and inspection. The number of technicians employed in each process and the amount of time they need to complete each process is displayed in the table below:

	Molding	Finishing	Inspection
Technicians	4	1	2
Technician time—Product A	4 minutes	5 minutes	3 minutes
Technician time—Product B	6 minutes	8 minutes	3 minutes

All technicians work 30-hour weeks.

Product A sells for $750 per unit and uses $200 per unit in direct materials. Product B sells for $1,200 per unit and uses $500 per unit in direct materials. Demand for Product A is 650 units per week, while demand for Product B is 500 units per week. Faerie currently manufactures 200 units of Product A and 100 units of Product B per week.

Currently, technician time in Finishing is the only constraint on production. Faerie could transfer a technician from Inspection to Finishing; if they do so, both Inspection and Finishing will be production constraints.

1. Determine the optimum product mix under current conditions.
2. Determine the optimum product mix if Faerie transfers a technician from Inspection to Finishing.

Optimum Mix Under One Constraint

Under current conditions, Finishing is the only constraint.

First, rank the products from highest to lowest in order of throughput margin per unit of constrained resource:

• Product A generates $750 – $200 = $550 in throughput margin per unit and uses 5 minutes of Finishing time. Throughput margin per minute is $550 / 5 = $110.
• Product B generates $1,200 – $500 = $700 in throughput margin per unit and uses
  8 minutes of Finishing time. Throughput margin per minute is $700 / 8 = $87.50
• Product A would be ranked first, followed by Product B.

Next, determine the units of each product in the optimum product mix:

• Fill demand for Product A if possible. Demand is 650 units, which uses 650 × 5 = 3,250 minutes. Currently, only 1,800 minutes are available, so Faerie does not have enough capacity to completely fill demand for Product A.
• Faerie should manufacture 1,800 / 5 = 360 units of A.
• The optimum product mix is 360 units of A and no units of B.
• Note that producing 360 units of Product A generates throughput margin of 360 × $550 = $198,000, which is higher than current throughput margin of 200 x $550 + 100 × $700 = $180,000.

Optimum Mix Under Multiple Constraints

If Faerie shifts a technician from Inspection to Finishing, both Inspection and Finishing will be constraints, but Molding will remain unaffected.

First, state the objective function:

• The variables are the number of units of Product A and Product B Faerie should produce; we will call those variables A and B.
• The objective is to maximize throughput margin.
• Mathematically, we state the objective: Max $550A + $700B.

Next, set up inequalities for each of the constraints (note that because Molding is not a constraint, it is not included):

• The time used in each department to produce A and B must be less than department capacity, and production must be less than demand.
• Finishing: 5A + 8B ≤ 3,600
• Inspection: 3A + 3B ≤ 1,800
• Demand: A ≤ 650 and B ≤ 500

Next (optionally), graph the constraints, if it will help you understand the problem better.

Plot Product A on the x-axis and Product B on the y-axis:

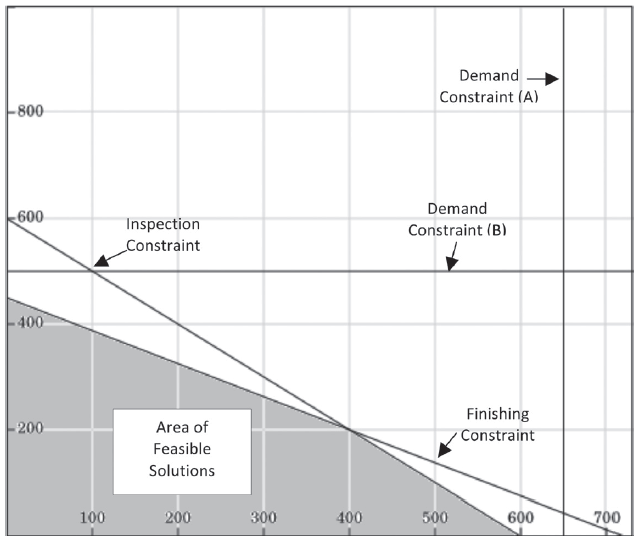
 Long description:

The x-axis represents the quantity of Product A, and the y-axis represents the quantity of Product B. The chart includes five constraint lines: a demand constraint for Product A, shown as a vertical line at 600 units; a demand constraint for Product B, shown as a horizontal line at 500 units; an inspection constraint, represented by a downward-sloping line intersecting the y-axis above 600; and a finishing constraint, another downward-sloping line intersecting the x-axis near 650. These constraints define a shaded triangular region labeled Area of Feasible Solutions, which contains all combinations of Products A and B that meet every constraint. This shaded area represents the solution space for determining the optimal product mix given limited resources and demand.

• The product mix must lie below and to the left of all lines, so the area of feasible solutions is bounded by the x- and y-axes, the Inspection constraint, and the Finishing constraint. As boundaries of the area of feasible constraints, the inequalities expressed earlier can now be expressed as equations for lines:
  • Finishing: 5A + 8B = 3,600
  • Inspection: 3A + 3B = 1,800

Next, find the corner points of the area of feasible solutions.

• Find the points where the constraint lines cross the x- and y-axes by plugging in zero for each product in each equation.
  • Finishing:
    • Plug in zero for A: 5 x 0 + 8B = 3,600 → (0, 450)
    • Plug in zero for B: 5A + 8 x 0 = 3,600 → (720, 0)
  • Inspection:
    • Plug in zero for A: 3 x 0 + 3B = 1,800 → (0, 600)
    • Plug in zero for B: 3A + 3 x 0 = 1,800 → (600, 0)
  • Eliminate the higher of the two x-intercepts and the higher of the two y-intercepts; these points lie outside the area of feasible constraints.
    • [(0, 450), (0, 600)] → (0,450)
    • [(720, 0), (600, 0)] → (600, 0)
• Find the point where the lines cross each other by solving the equations simultaneously. Transform one of the equations so the coefficient on one of the variables is the same as in the other equation. Then subtract one equation from the other.
  • Multiply [3A + 3B = 1,800] by 5/3 → 5A + 5B = 3,000
  • [5A + 8B = 3,600] – [5A + 5B = 3,000] = [0 + 3B = 600] → B = 200
  • Plug in 200 for B in either equation: 5A + 8 x 200 = 3,600 → A = 400
  • The points cross at (400, 200)
• The points at the corners of the area of feasible solutions are (0, 450), (400, 200), and (600, 0).

Finally, plug the corner points into the objective function to determine which mix earns the most throughput margin.

• (0, 450): 0 × $550 + 450 × $700 = $315,000
• (400, 200): 400 × $550 + 200 × $700 = $360,000
• (600, 0): 600 × $550 + 0 × $700 = $330,000
• The best mix is 400 units of A and 200 units of B.