18 Advanced Investment Analysis

The Theory

Tools such as net present value and internal rate of return are useful in evaluating a long-term investment project when it is expected to unfold as initially planned. Traditional discounted cash flow methods can incorporate multiple possible outcomes into an analysis by finding the expected value of the cash flows involved. However, when long-term projects involve choices to be made by management as the project unfolds, traditional discounted cash flow methods are not designed to account for the additional value that these choices produce.

Expected net present value analysis (ENPV) allows decision makers to incorporate uncertainty into discounted cash flow analysis. Basically, the present value (PV) of each particular outcome is multiplied by the probability that it will happen. These values are then summed to find the expected net present value of the project.

Real options analysis (ROA) goes a step further than expected net present value analysis by allowing decision makers to incorporate the choices managers can make at various stages of a project. When managers can make choices as a project unfolds, the project is worth more than when managers have no choices. Such choices are called real options. The value of real options can be calculated in a number of ways, including using techniques designed for calculating the value of financial options. However, their value can also be calculated in simpler ways, such as by using decision trees.

A decision tree is a diagram mapping out decisions and alternative outcomes, including the probability that each outcome will occur:

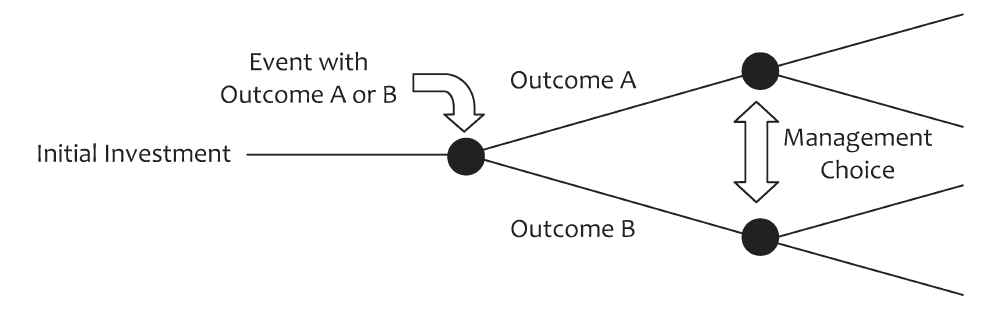
Image long description:

The tree begins with an initial investment, followed by an uncertain event with two possible outcomes: Outcome A or Outcome B. Each outcome leads to a decision point represented by a black circle, where management must choose among multiple options. Arrows between the nodes for Outcome A and Outcome B indicate that managerial decisions are contingent on the outcome that occurs. This structure reflects the essence of real options analysis—valuing the flexibility to make future decisions based on how events unfold.

When a decision tree is used to calculate the value of real options, the value of each outcome is added to the tree. These values and their probabilities are then used to calculate the expected value of the project given the best choices management could make at each decision node.

Typical real options that arise in long-term investment projects include the option to defer an investment until more information is available, the option to expand an investment or launch future investments if the project is successful, and the option to abandon a project if it is unsuccessful.

The Method

Expected Net Present Value Analysis

For each possible outcome of the project, multiply the present value of the future cash flows associated with that outcome by the probability it will occur. Then, add the result for all possible outcomes of the project, and subtract the net initial investment from that total. (Note: The probabilities of all possible outcomes should total 100%). Just as in net present value analysis, projects with a positive value earn more than the firm’s required rate of return.

Real Options Analysis

First, identify the possible outcomes and the firm’s available choices. For each possible outcome, the firm could have several choices. It is often helpful to illustrate these outcomes and choices using a decision tree.

Next, determine the present value of cash flows for each possible scenario. It is often helpful to use a timeline to illustrate when cash flows occur. Discount all future cash flows to the present point in time, using present value factors based on the required rate of return.

Next, determine which decision the firm will make on each branch of the decision tree. The firm will make the decision that yields the higher present value for that branch. Eliminate any scenarios the firm will not choose.

Next, calculate the value of the project. Multiply the present value of each possible outcome by its probability, then add them together and subtract the initial investment. Just as in net present value analysis, projects with a positive value earn more than the firm’s required rate of return.

Finally, calculate the value of any real options associated with the project by finding the difference between the project’s value including real options and its expected net present value.

Illustrative Example

Trafalgar Electronics is considering marketing a product designed by their Research and Development department. The project will require an investment of $100,000 to build the production technology. This production technology could be sold at 55% of its investment value if the project is discontinued. The marketing department has reported that the project’s expected cash flows will depend on demand. There is a 60% chance that demand for the product will be high, with net cash flows of $60,000 per year, and a 40% chance that demand will be low, with net cash flows of $10,000 per year (we will learn which outcome will occur within days of the product launch). The project is expected to last 5 years. The company’s required rate of return is 15%.

Calculate the net present value of the project using the expected value of its future cash flows. Then, calculate the value of the project using real options analysis.

Expected Net Present Value Analysis

Multiply the present value of the cash flows associated with each outcome by the probability that it will occur, and total the results:

• Present value factor for a 5-year annuity at 15%: 3.3522
• PV of future cash flows if demand is high: $60,000 × 3.3522 = $201,132
• PV of future cash flows if demand is low: $10,000 × 3.3522 = $33,522
• Expected value of future cash flows: $201,132 × 60% + $33,522 × 40% = $134,088
• Expected net present value of project: $134,088 – $100,000 = $34,088

Real Options Analysis

First, identify the possible outcomes and the firm’s available choices:

• The possible outcomes are that demand could be high or low.
• The firm could choose to continue the project, or they could abandon the project and sell the assets for 55% of their value once they know whether demand is high or low.

Next, determine the present value of cash flows for each possible scenario:

• As calculated under the expected net present value analysis:
• • PV of future cash flows if demand is high: $60,000 × 3.3522 = $201,132
  • PV of future cash flows if demand is low: $10,000 × 3.3522 = $33,522
• PV of future cash flows if the project is abandoned: $55,000 (already at present value)

Next, determine which decision the firm will make on each branch of the decision tree:

• If demand is high, the firm will choose to continue the project, as the present value of continuing ($201,132) is higher than the present value of abandoning ($55,000).
• If demand is low, the firm will choose to abandon the project, as the present value of abandoning ($55,000) is higher than the present value of continuing ($33,522).

Next, calculate the value of the project:

• PV of future cash flows if demand is high (the project is continued): $201,132
• PV of future cash flows if demand is low (the project is abandoned): $55,000
• Expected value of future cash flows: $201,132 × 60% + $55,000 × 40% = $142,679.20
• Value of project: $142,679.20 – $100,000 = $42,679.20

Finally, calculate the value of any real options associated with the project:

• The value of the option to abandon the project is $42,679.20 – $34,088 = $8,591.20

Lecture Example

Multicorp is considering marketing a new product that will require an investment of $1,000,000. The product will have a life of 5 years and is expected to produce income of $450,000 each year. However, there is a 10% chance that a competitor will beat Multicorp to market with a similar product, in which case cash flows will only be $200,000 each year. If Multicorp were to discontinue the product, they could license the technology to another firm, which would result in a one-time cash flow of $800,000. The company’s required rate of return is 12%.

1. Calculate the expected net present value of the project.
2. Calculate the value of the project using real options analysis.
3. Calculate the value of the real options associated with the project.