Maximizing genetic gain III
Walter R. Fehr and Walter P. Suza
Readings:
- Chapters 6 and 7 [PDF], Principles of Cultivar Development. Vol. 1: Theory and Technique, by Walter R. Fehr (Access the full book)
- Chapter 15 [PDF], Principles of Cultivar Development. Vol. 1: Theory and Technique, by Walter R. Fehr
- Chapters 17, 18, and 19 [PDF], Principles of Cultivar Development. Vol. 1: Theory and Technique, by Walter R. Fehr
Introduction
The Applied Learning Activity for this lesson is intended to give you experience in applying the principles that are discussed in the reading assignment. The answers you obtain should be useful for understanding the options a breeder has for maximizing the amount of genetic gain per year with the resources available.
The genetic gain equation was developed as a method of comparing methods of recurrent selection. As indicated in chapter 15 of Principles of Cultivar Development, classical recurrent selection means that once a segregating population is formed, only superior progeny from the population are crossed together to begin the next cycle of selection.
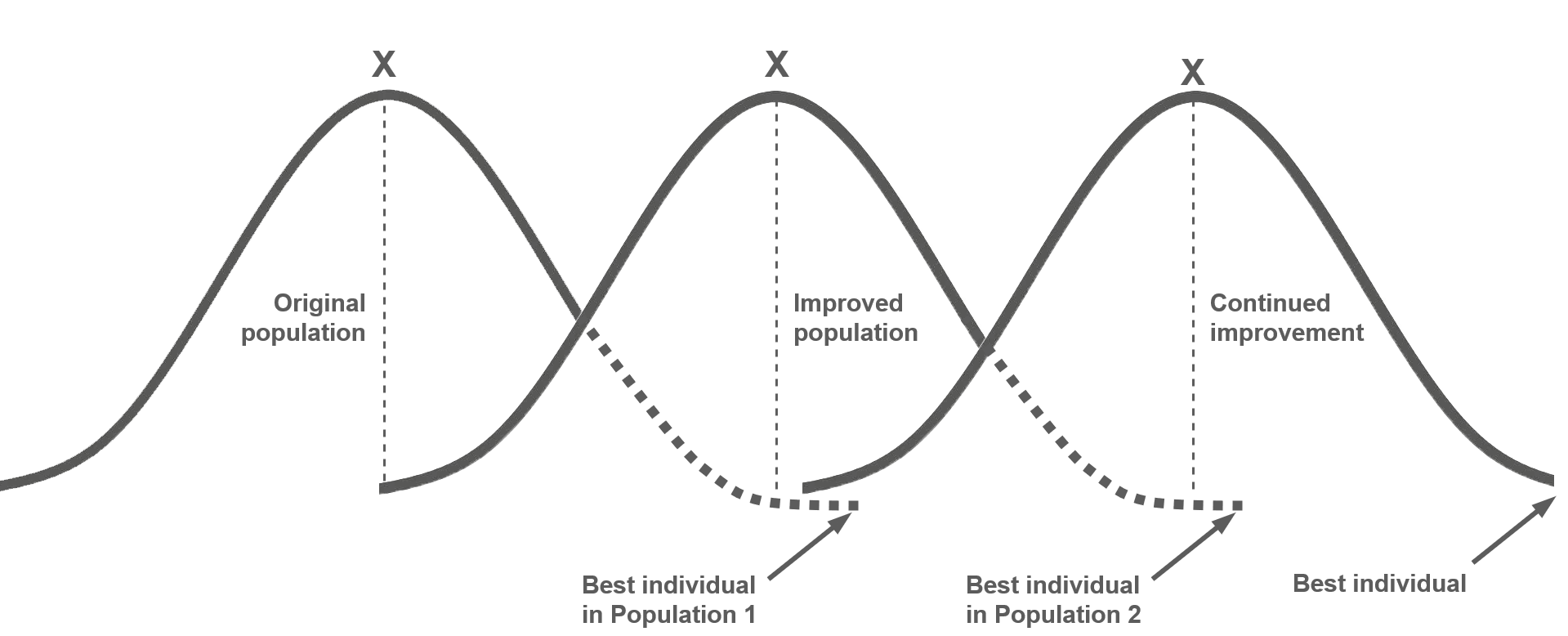
Although this is done, many breeders would say that any breeding program is essentially recurrent selection, even though superior progeny from different populations and sources are used to form their new segregating populations for selection each year. With regard to the valuable principles that can be learned from the genetic gain equation, it does not matter if a breeder is conducting classical recurrent selection with closed populations or a more traditional breeding program in which the superior progeny identified each year from multiple populations are used to form new populations.
The values for each of the components in the genetic gain equation vary with every breeding population, quantitative trait, and plant species. You will learn more about how to derive the components in your statistics courses and in the course on population and quantitative genetics for breeding. The critical thing to learn in this lesson is how the breeder can influence the magnitude of each component in the equation to maximize genetic gain per year.
In the section of Plant Breeding Methods dealing with recurrent selection, it was pointed out that the methods of recurrent selection of practical use for a plant species depend on the type of cultivar under development. Applied Learning Activity 3 assumes that all of the methods are practical to use for a species, so that you can see how the estimated genetic gain can vary.
The practical experience of the breeder plays a major role in making decisions about the methods of recurrent selection that are the more effective. For example, the use of selfed families is possible for population improvement in crops for which hybrids are used commercially, such as maize. However, research has demonstrated that the amount of genetic gain per year for the yield of hybrids in maize is less when selfed families are used for evaluation than when individuals are evaluated as half-sib families for their combining ability. This is consistent with how breeders conduct a breeding program for developing improved inbreds, as will be discussed in the section on hybrid cultivars. Breeders rely on tests of combining ability for yield, instead of on the yield of an inbred line per se.
One of the most important principles that the genetic gain formula teaches is the importance of completing a cycle of selection as rapidly as possible, regardless whether you are doing classical recurrent selection or more conventional breeding. It is the genetic gain per year and not the genetic gain per cycle that is critical. That is why modern plant breeding programs make such extensive use of off-season nurseries to reduce the number of years it takes from the time a cross is made to form a segregating population until superior individuals from the population have been selected for use as parents to form new populations. One plant breeding myth is that it does not matter how long it takes to develop a cultivar, as long as you have new ones to release on a consistent basis. This myth fails to take into account the importance of genetic gain per year. Over a 24-year period, a breeder who takes only four years from crossing until superior progeny are ready to use as parents will make substantially more genetic gain than a breeder who takes eight years to complete a cycle.
When you prepare for the mid-term and final exam of this course, be sure you can write out the entire formula for genetic gain per year and can explain how you as a breeder can influence the magnitude of each of the components in the formula.
Applied Learning Activity 3
You have the following estimates available for making the calculations required in this problem. The relative magnitude of the additive genetic variance and the additive x environment interaction versus the dominance genetic variance and dominance x environment interaction varies among traits. For this problem, assume that the genetic variance is divided equally between the additive and dominance variance ie. 82 for the additive and 82 for the dominance variance. For the genotypic x environment interaction, assume that the additive x environment and the dominance x environment both equal 48.
[latex]\sigma^{2}_{u}=1280 \qquad \sigma^{2}=184 \qquad \sigma^{2}_{ge}=96 \qquad \sigma^{2}_{g}=164[/latex]
Your research manager wants you to evaluate alternative methods of recurrent selection that could be used to improve a population for an important quantitative character. For genotypic evaluation, assume that lines are evaluated in two replications with 30 plants per plot at each of five locations. The selection intensity is 10% for all methods.
- Compute genetic gain per cycle for the following methods. Put your answers in the table below. The gain should be expressed to the nearest 0.1.
-
- Recurrent phenotypic selection – selection before flowering with gridding
- Recurrent phenotypic selection – selection after flowering without gridding
- Half-sib selection, population as tester, recombine with half-sib seed
- Half-sib selection, inbred tester, recombine with selfed seed. Assume [latex]\sigma^{2}_{g}= 1/4 \sigma^{2}_{A}[/latex]
- S0:1 line evaluation – 1 intercrossing generation between cycles
- S2:4 line evaluation – 2 intercrossing generations between cycles
- Compute gain per year for each of the six methods in part A under the following circumstances. The gain should be expressed to the nearest 0.1. To determine the number of years required to complete a cycle of selection for each of the methods and seasons, it is best to count the number of years it takes to go from the season of testing individuals from the cycle 0 population until you begin testing individuals from the cycle 1 population.
For example, assume you are evaluating half-sib selection with the population as the tester and have only season per year available. If a test of the half-sib families from cycle 0 was done in Ames during 2012, you would select your best individuals based on data collected by the end of the year, cross the best individuals to form new half-sib families of cycle 1in 2013, and select the best individuals from cycle 1 based on data for half-sib data collected by the end of 2014, which would be two years per cycle. On the other hand, if you had two similar seasons each year, you could test the half-sib families for cycle 0 in Ames during 2012, use the selected individuals to form new half-sib families of cycle 1 during a winter season in Hawaii, and test the new half-sib families during 2013, which would be one year per cycle. It helps in determining the number of years per cycle to make up locations of your choice for each of the scenarios below. Keep in the mind that in some of the scenarios, the number of years per cycle can be part of a year, such as 1.5.
-
- One season per year for testing, crossing, or selfing
- Two similar seasons per year. Testing, crossing, or selfing can be done in any season
- Two non-similar seasons per year. Testing is possible in only one season, but crossing and selfing can be done in both seasons.
- Three seasons per year. Testing, crossing, or selfing are possible in one season, followed by two consecutive seasons in which only crossing and selfing are possible.
| Method | Gain per cycle | Gain per year (1 season) | Gain per year (2 similar seasons) | Gain per year (2 non-similar seasons) | Gain per year (3 seasons) |
|---|---|---|---|---|---|
| a. | |||||
| b. | |||||
| c. | |||||
| d. | |||||
| e. | |||||
| f. |
- Which of the methods would you choose for the four circumstances below? Consider amount of gain per year and cost of the gain for the six methods.
- One season per year
- Two similar seasons per year
- Two non-similar seasons per year
- Three seasons
References
Fehr, W. R. (ed). 1987. Principles of Cultivar Development. Vol 1. Theory and Technique. McGraw-Hill, Inc., New York.

