Part I. PROBLEM SOLVING
3. A Solved Problem
3.1 Problem background: the tilted tape
Students completing a stream physical habitat survey measure geometry and record characteristics of wadeable stream channels and the adjacent banks and floodplains. Among the common measurements included in these surveys is a stream cross-section. A stream cross-section often includes topography, vegetation cover, water depth, and particle size characterization, observed at regular increments from the top of one bank to the top of the other. Topography is sometimes measured with cloth measuring tapes, optical levels and stadial rods, high-end GPS receivers, or total stations. In remote settings or when precision instrumentation is not available, a single cloth tape and a telescoping stadial rod can achieve results that are usually very adequate.

A common procedure for rod-and-tape cross-section measurements, illustrated in Figure 3.1, is as follows:
- Secure the ‘0’ end of the tape to a stable fixed point (e.g., a tree trunk or fence post) on the floodplain or hillside above the left bank (facing downstream), ensuring that the tape is secured at a height that is greater than any points to be measured in the cross-section.
- Stretch the tape across the stream so that it is perpendicular to streamflow.
- Secure the reel side of the tape to a stable fixed point on the floodplain above the right bank. Take care to make the tape as taut and level as possible, so that the elevation of both ends of the tape is equal and the tape does not sag. Use a carpenter’s level or handheld clinometer if available.
- At regular intervals along the tape (typically every 0.5 or 1 meter, depending on stream size) stand the stadial rod vertically on the ground or streambed and record the height on the stadial rod where the tape crosses. In addition, make measurements at key points along the way, such as the top of the streambank, edge of water, and the deepest place in the channel.
- At each station, note the landform or feature at that station, record vegetation type and density, soil texture or properties, water depth, habitat features, and sediment size, as appropriate.
- Back in the office or classroom, convert the rod-height readings to elevations by subtracting the rod readings from a known or arbitrary elevation datum.
| sta. (m) | elev. (m) | feature |
|---|---|---|
| 0.5 | 329.48 | |
| 1.05 | 328.59 | Left BF |
| 1.15 | 328.16 | |
| 1.74 | 327.94 | Left EOW |
| 2.0 | 327. 87 | |
| 2.5 | 327.9 | |
| 3.0 | 327.94 | |
| 3.5 | 327.86 | thalweg |
| 4.0 | 328.0 | |
| 4.5 | 327.99 | |
| 5.0 | 328.01 | |
| 5.5 | 328.0 | |
| 6.0 | 328.07 | |
| 6.17 | 328.09 | Right EOW |
| 6.58 | 328.60 | Right BF |
| 7.0 | 328.97 | |
| 8.0 | 329.51 | |
| 8.48 | 330.0 |
This low-tech method can produce very accurate data, but it can also be susceptible to errors. One commonly-encountered problem is that the tape is not perfectly level when stretched across the stream. This problem is not often recognized until after the data is collected. Indeed, it is often only noticed when the rod-heights from the left and right edge of water appear to be significantly different. Table 3.1 shows a dataset in which this If observations from the channel indicate that channel features (such as a gravel bar) caused real water elevation to be higher on one bank than the other, this may not be an error. In most cases, however, this indicates that the tape was not precisely level. Can we still use this topographic data, or does it need to be discarded?
Problem statement
Take the optimistic view that the topographic cross-section data can still be used. Devise a strategy for correcting the error that causes the left and right edge-of-water (EOW) heights to be unequal. Use your strategy to correct for tape tilt in the data from Table 3.1.
3.2 Elements of a solution
Our first task is always to make sure we understand the problem, and even if this appears at first to be trivial. Consulting our problem solving tips from Chapter 2, we should begin by addressing some of the questions under “Understand”. Do we understand the problem as stated? A good test of this is to attempt to restate it in our own words. Let’s try:
We have data from a tape-and-rod stream cross-section survey where the elevation of the left and right waterlines isn’t equal. We assume that within a single cross-section the water surface is flat, so we infer that the tape that was used to read elevation from the rod was not quite horizontal. We need to figure out if there is a simple way to correct the data after the survey is complete.
How have we done? Is this roughly how you interpret the problem? If not, rephrase it as you understand it. Just because your instructor describes it one way, that doesn’t mean that’s how it will best make sense to you.
Continuing with “Understand”, what should we be looking for in a solution? Well, the problem statement specifically asks for corrected data from Table 3.1, so this means we’re looking to adjust the data in the “elevation” column. The statement also calls for a strategy or procedure, so we need to think about not just getting the numbers adjusted, but also formally documenting the procedure. Since stream ecologists and geomorphologists make cross-section measurements frequently, developing a re-usable procedure could greatly streamline the processing and quality control of the data.
This problem is one for which a drawing could be really helpful, particularly as a way to visualize how the tilted tape could cause issues with the data. A drawing in this case could also be a useful way to organize information visually. But even here, we have some consequential decision to make. Do we want to try to make a drawing that accurately reflects the numbers in the problem, or do we want our drawing to serve as more of a sketch where we can distort things so it’s easier to “see” important features of the problem? Our heuristic from the last chapter suggested that we should make the drawing as accurate as possible. In this case, however, an accurate representation might actually be difficult to sketch in a way that is useful for visualizing problem information. Compare the two sketches in Figure 3.2. Which one is more accurate? Which one is more useful for organizing information?
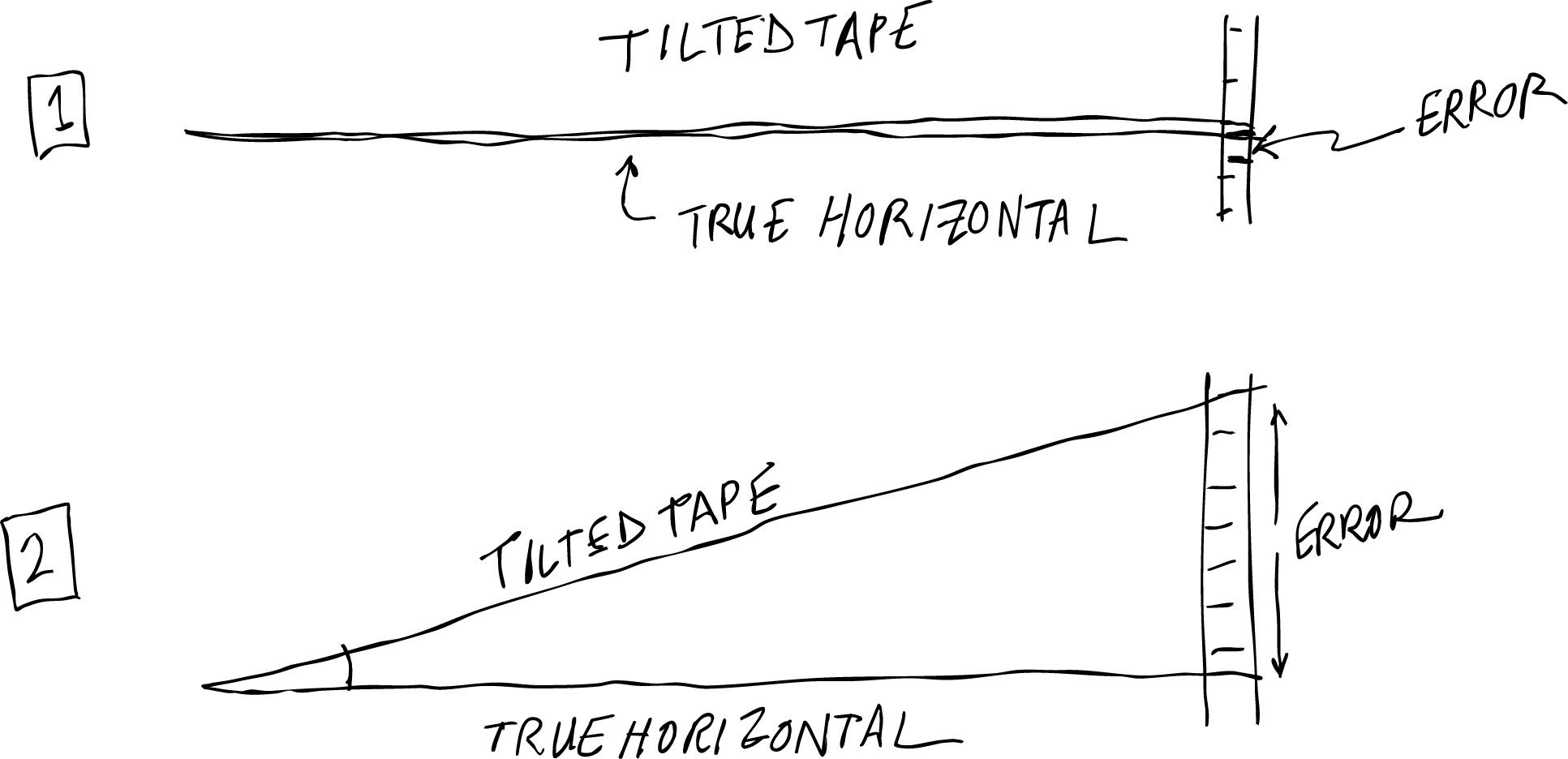
While sketch 1 may be perhaps more accurate, it is harder to see and play with the issues involved. For the purpose of understanding the problem, sketch 2 may therefore be more useful. Perhaps once we’ve wrapped our minds around what we’re doing and why, a more accurate sketch can be useful for communicating. Heck, unless we’re short on paper there’s no particular reason to restrict ourselves to just one drawing, so let’s plan to make several.
So sketch 2 with exaggerated dimensions allows us to organize information that may be helpful in addressing relevant questions remaining in “Understand”. Do we know what reasonable values should be for the corrected elevations? Sort of. A quick look at the edge of water (EOW) elevations in Table 3.1 makes clear that the mis-match between left and right edge elevations is 328.09 m – 327.94 m, or 0.15 m (15 cm). So our correction should change some elevations by something like 15 cm, probably not way more than a meter and probably not much less than 1 cm. This ballpark range also gives us a sense for how accurate we need to be. If we’re concerned about mismatches in elevation of 15 cm, then we probably care about elevations at least down to the nearest 1 cm. Anyhow, minnows, crayfish and shorebirds probably care about differences in water depth of a centimeter!
Suppose we add some of this information to an updated version of our sketch. Here we may need to be creative and maybe even forge ahead toward a preliminary solution plan. Since the left EOW appears to be lower than the right EOW in the uncorrected data, one reasonable goal could be to try to figure out a solution procedure that lowers the right EOW by 15 cm. OK, but wait! Why not instead raise the left edge by 15 cm, you say? Indeed, why not? Here we encounter that uncomfortable feeling of uncertainty. We may be tempted at times like this to turn to the instructor with a question like “Are we supposed to…?”. But as we’ve already established, there are often no “supposed to’s” in real problem solving. That leaves us with a need to assume more control, and in some cases that is an unpleasant and stressful feeling. But why shouldn’t we view this as liberating instead? We finally have an opportunity to dictate what the correct procedure is. It will be a correct procedure as long as we can verify that it yields an accurate and reproducible solution to the problem, the computations follow the rules and logic of mathematics, and provided that we clearly articulate any assumptions or conventions our procedure relies on.
Let’s take stock of where we are now. We have restated the problem in our own words, defined the outcomes we seek, made some sketches that help us organize the information we have, and identified a need to make some decisions about how we will incorporate given information into a plan and solution.
Before we jump into planning, let’s establish some criteria that we can use to decide whether a solution that we arrive at satisfies the statement of the problem. Here we’re setting up a framework for “Check” that we can come back to later and adjust if necessary, but it can be a helpful reminder of what we’re after and a test of whether we’re on the right track. A satisfactory solution should:
- correct elevations in Table 3.1 so that the left EOW and right EOW elevations are equal.
- be self-consistent and reproducible.
- be generalizable so that the same procedure can be applied to other cross-section data sets.
Now that we have our ducks in a row, we can work toward a solution plan. Our latest sketch hints at an idea: if we assume that the left end of the tape is at the “correct” elevation and the right end was fixed a bit too high, can we rotate all of the elevations around the zero point on the tape until the left and right EOW elevations are equal? How do we rotate a bunch of data points though, and how much rotation is necessary? Well, these are really important questions, and here’s where we can’t just reason our way through a solution without recruiting some resources. By resources, we mean some recollection of how to mathematically describe angles and rotation. You may have encountered some of these concepts in earlier classes, but if not you’ll see them later in this book.
For now, let’s use the most straight-forward resources that we think might be relevant to this problem. Let’s interpret the tilted tape as a line in the cross-section plane that has a slope different from the horizontal. Recall that we can define slope as “rise over run”. In this context, we can interpret rise over run as a change in elevation with distance from a reference point. But how do we use that with the information we know? Let’s imagine that the reference point is at the left EOW point in the cross-section (Figure 3.3). We know that the right EOW is 0.15 m higher than the left, so let’s interpret that as the rise. The distance between the left and right EOW on the tape is 6.17 m – 1.74 m = 4.43 m, so that’s the run. The slope, then, is 0.15 m/4.43 m = 0.03386. Notice that I didn’t put units on the 0.03386; that was deliberate, because the units of our rise-over-run quotient cancel out.
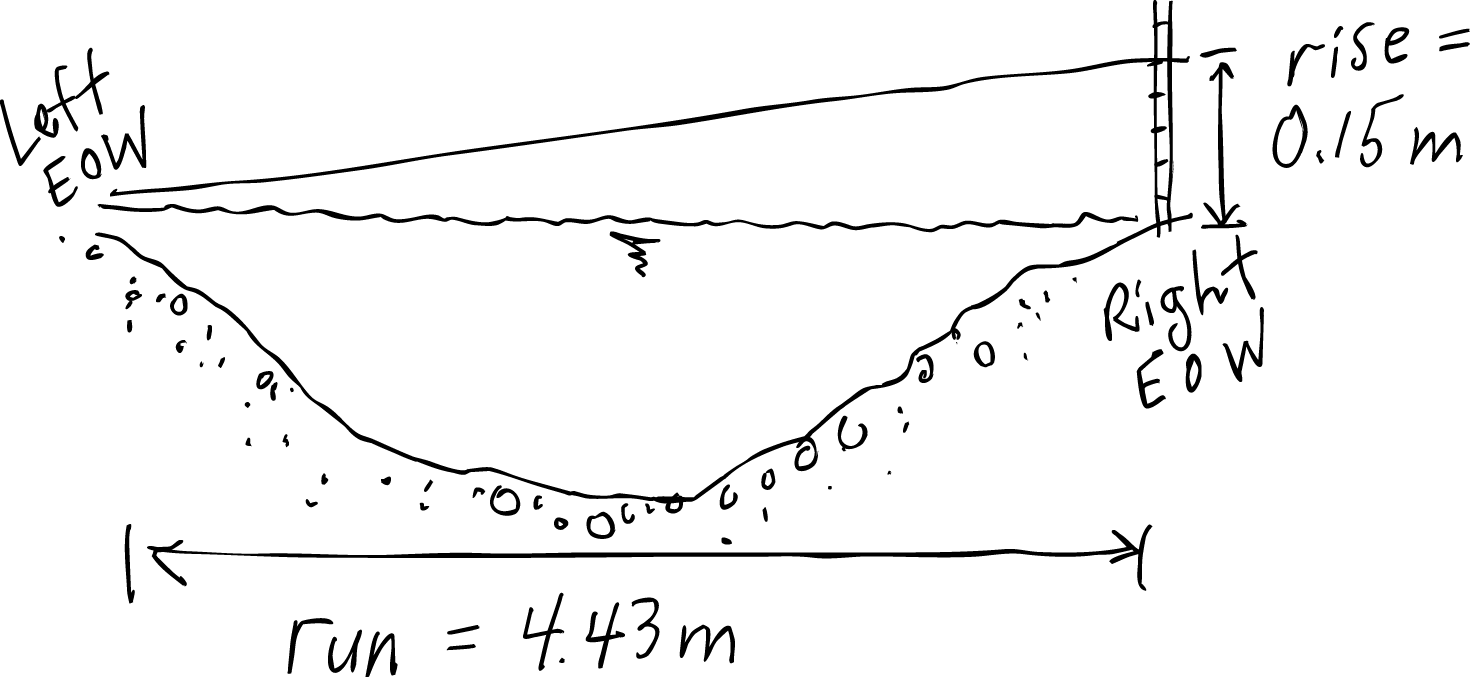
What have we just done? We haven’t solved the whole problem, right? We haven’t satisfied any of our solution criteria yet, right? But we have taken a step in that direction along a potential solution pathway. We could say that one thing we’ve done is to find an important quantity (the amount of tilt, measured in terms of slope) that might help us advance. This is effectively a sub-problem within the larger problem, and that’s one of our general heuristics. But thus far we may have done this blindly. That’s OK, if we’re stumped on a plan it’s OK to try a few things and see what happens. But if we aren’t stumped, we might want to step back and think about how this little exercise serves the overall goal of solving the problem. How will we use the “slope” quantity?
Consider this: since slope is rise over run, if we decide to choose a fixed value for slope, the ratio rise over run is also fixed, even if we vary the rise and run. But rise and run need to vary in such a way that their ratio is always equal to that same fixed slope value, in this case 0.03386. If we imagine a run of 1 meter, the rise over that distance that makes for a slope of 0.03386 is just 0.03386 m, or around 3.39 cm. Stated as an equation, if we define [latex]S[/latex] as slope, [latex]y[/latex] as run, and [latex]z[/latex] as rise:
[latex]S = z/y[/latex].
If we rearrange this so that we solve for z and substitute our fixed slope value [latex]S = 0.03386[/latex]:
[latex]0.03386 y = z[/latex].
We’ve just done some fairly abstract thinking and a bit of algebra, so let’s take a minute to absorb it.
Making the leap from defining slope as rise over run to writing an equation in terms of [latex]S[/latex], [latex]y[/latex], and [latex]z[/latex] is a way of thinking that might not come naturally to some people. We had to temporarily let go of the concrete idea that rise, run, and slope are particular characteristics of a tilted cross-section with particular associated numbers that come from our dataset, and instead treat them more abstractly as symbols. In doing this, we have generalized from the specifics of our real problem to an abstraction that may appear unrelated. Why? Because abstraction, or in this case generalization, of the relationship allows us to write a formula that can be re-used to convert any [latex]y[/latex] value (station on the tape) to a corresponding [latex]z[/latex] value for the sloped tape! If we choose a [latex]y[/latex] value that is half of the width of the wetted channel (2.215 m), then the corresponding [latex]z[/latex] from our slope formula should be half of 0.15 m, so 0.075 m, right?
Hang on! Let’s think back to what [latex]z[/latex] meant before we generalized. This was the amount that one water’s-edge point appeared to be higher than the other. What if we just subtract [latex]z[/latex] from all the elevations in our dataset, using the station as [latex]y[/latex]? Let’s try it! But how? There are 18 numbers in the elevation column of our data table. It would be possible, but tedious, to do this all by hand with a pocket calculator. If we can use a spreadsheet, that would be more efficient.
Copying the data from the table above into a spreadsheet is tedious too, but once we’ve got the structure set up and provided that we know some shortcuts, it’s not so bad. With a simple cell formula and a fill command, we’ve got a result (Table 3.2).
| station (m) | elev. (m) | corrected elev. (m) | feature |
|---|---|---|---|
| 0.5 | 329.48 | 329.48 | |
| 1.05 | 328.59 | 328.57 | Left BF |
| 1.15 | 328.16 | 328.14 | |
| 1.74 | 327.94 | 327.90 | Left EOW |
| 2.0 | 327. 87 | 327.82 | |
| 2.5 | 327.9 | 327.83 | |
| 3.0 | 327.94 | 327.86 | |
| 3.5 | 327.86 | 327.76 | thalweg |
| 4.0 | 328.0 | 327.88 | |
| 4.5 | 327.99 | 327.85 | |
| 5.0 | 328.01 | 327.86 | |
| 5.5 | 328.0 | 327.83 | |
| 6.0 | 328.07 | 327.88 | |
| 6.17 | 328.09 | 327.90 | Right EOW |
| 6.58 | 328.60 | 328.59 | Right BF |
| 7.0 | 328.97 | 328.75 | |
| 8.0 | 329.51 | 329.26 | |
| 8.48 | 330.0 | 329.73 |
Great, we’re done right? Well no. While it may be tempting to just get a result, submit it and leave, we still need to check our result. The first step is probably to look at the spreadsheet and ensure that our data entry was correct, the formulas are correct, and that our numbers are reasonable. Next, recall that we laid out three criteria for a satisfactory solution. This gives us a clear set of expectations:
- Do our corrected numbers make the left EOW and right EOW elevations equal? YES.
- Is our solution self-consistent? YES, provided that a double-checking of the numbers yields no errors. Is it reproducible? YES, because we implemented it in a spreadsheet and kept breadcrumbs from our steps.
- Is it generalizable? PERHAPS. If we use the definition of slope to identify the tilt in another setting and a version of our elevation correction equation modified for the appropriate [latex]S[/latex], this could be generalized into a versatile sequence of clear steps. This is left as an exercise for you to do.
So it looks as though we’ve done pretty well!
A final step in problem solving in many cases is to report the solution to those who need to see or use it. We’ll look into some of the issues involved in reporting quantitative information later in this book, but a few things should be highlighted here. Most importantly, there is sometimes room for slightly or significantly different interpretation of the problem to begin with. In the process of understanding the problem, we made some assumptions or inferences and proceeded as though they were true. In problems that invite alternative interpretations of the data or the context, this can lead different people to very different solutions. How are we to know who is correct or whose solution is more reliable then? By scrutinizing the assumptions made in finding a solution, we can select the solution with fewer or better assumptions! If the assumptions are not articulated as part of the solution statement, we may have a hard time trusting the solution.
Exercises
- There is at least one error among the corrected elevations in Table 3.2. Identify which entry or entries have errors and provide a corrected value.
- Using a word processor and its built-in equation typesetting tool, write down a generalized set of steps for performing these corrections that can be used as a standard protocol for data quality assurance for students making and reporting stream cross-section measurements.
- As with most authentic problems, there is more than one way to obtain a solution. Instead of using the slope strategy that we demonstrated above, can you suggest an alternative approach to making corrections?
- We have envisioned our solution in terms of an imagined “rotation” of the tape around the zero point. Do you think that the algebraic statement we used to make corrections provides an accurate correction? Hint: Suppose that the tape was actually tilted at a much greater angle, say 25º. Does the distance reading y on the tape really correspond to the horizontal distance across the channel? If not, by how much is it off in our analysis above? Is this error acceptable?

