Part III. SPATIAL REASONING
9. Geometry and Geography
One of the fundamental types of quantities that we use as natural resource scientists and professionals is a measure of distance or size. Whether we’re describing the board-feet of merchantable lumber in a ponderosa pine, the fork length of a trout, the size of a whitetail deer’s home range, or the storage capacity of a flood-control reservoir, we are concerned with spatial quantities that ultimately manifest from linear measurements in space. Much of this may feel familiar to you, but there are important messages to take home from working with both simple and compound spatial quantities that will serve you well in working with maps, photos, design plans, and other tools that professionals use.
9.1 Length, Area, and Volume
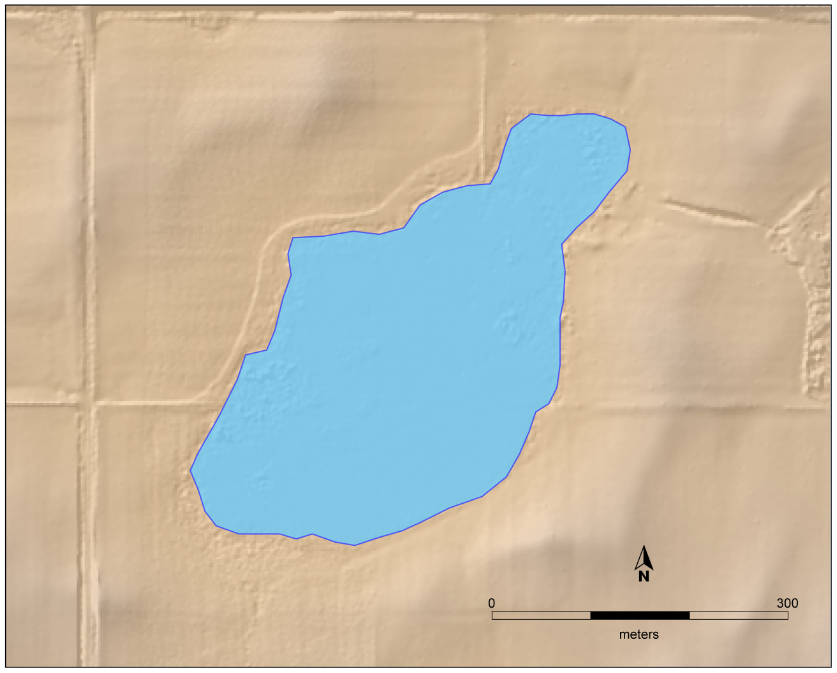
Consider the wetland shown in the map below (Figure 9.1). How might we characterize its size? Perhaps the answer depends on the context of the question. Are we interested in how far it is to cross it in a canoe? How long the shoreline habitat is for waterfowl? The number of acres it occupies? What about the amount of water it holds? In turn these questions point to linear distance, curvilinear distance, area and volume, respectively. Each of these types of quantities can be expressed in a variety of ways according to the setting, the application, or the purpose of communication.[1]
The distinctions between length, area, and volume are more than just trivia. They clearly reflect not only different ways of estimating size, but different numbers of spatial dimensions. In common parlance, length is one-dimensional or 1D, area is two-dimensional or 2D, and volume is three-dimensional or 3D. The units can be a clue to how many dimensions are indicated in a spatial description. From Chapter 4, recall that we can generalize units in terms of the fundamental dimensions they entail. From this perspective then, a 1D length has dimensions of [L], a 2D area [L2], and a 3D volume [L3].
This is true regardless of the specific units used to describe the quantity of interest, though sometimes the dimensionality can be obscured by the use of compound units. For example, if we’re told that a woodlot is 820,000 ft2, that is a straight-forward 2D measure of area. If that same woodlot is described as 126,000 board feet,[2] now we’re talking about a volume of wood expressed in a unit that is not particularly transparent to outsiders, though it is customary among foresters. If we need to do computations involving quantities of this sort we need to be certain that we understand what makes sense and what doesn’t make sense to do; what’s permissible and what isn’t.
Note that some of our commonly-used spatial units are compound by definition. An acre, for example, is a unit of area even though it is not expressed in a squared-length form. Originally defined as the area of land that could be plowed with oxen in a day, an acre is 43,560 ft2 or roughly 4,047 m2. If you measured out a square 208.7 ft on a side, that would be approximately an acre. The acre’s cousin in SI units, the hectare, is also a unit of area with a simpler definition: an area of land 100 m wide and 100 m long, or 10,000 m2.[3]
We’re also familiar with several alternative ways of expressing volume with derived units, particularly when talking about liquids. It’s not unheard-of to talk about fluid volumes in cubic meters or cubic feet (particularly if we’re referring to volume per unit time as we do when describing river flows in cubic feet per second or cfs), but it is more common to hear fluid volumes expressed in gallons, millileters or liters. These are all legitimate expressions of fluid (gas or liquid) volumes and some have relatively straight-forward relationships to length-cubed volumes: for example, 1 ml is the same as 1 cm3 or cc. However, if we wish to perform computations more complex than addition or subtraction on such quantities, it can be advantageous to convert them into more fundamental units like cubic meters. One interesting unit of volume mentioned above is the acre-foot, which (as you might guess) is the volume corresponding to a one acre area of something that is one foot deep. This means its dimensions are an area [L2] times a depth [L], therefore it is a volume [L3]. We encounter this unit of volume sometimes in descriptions of ponds or stormwater-basins because it may be easier to visualize, but this can also make it more difficult to perform computations.
9.1.1 Unit conversions in space
Here’s an common exercise that American students often need to perform in earth science, geography or natural resource courses: measure a rectangular land area on a USGS map with a scale in feet and miles, and convert it to square meters or square kilometers.[4]

This exercise will typically begin with each student begrudgingly making tickmarks on the edge of a sheet of paper that is lined up with the map scale. For purposes of illustration, we’ll follow the hypothetical (but not uncommon) path of a student who is prone to making some common mistakes. Our student uses the marked paper to estimate the length of each side of the rectangular land area using the scaled map units.[5] Perhaps the values are 6.2 miles and 2.1 miles. He then proceeds to multiply them together, because he’s aware that the area of a rectangle is the product of its sides. So he punches [latex]6.2 \times 2.1[/latex] into his calculator and gets 13.02. When asked to supply units for his answer, he reasons that since the units he was measuring distances in were miles, the answer is also in miles.
His instructor points out that miles are a unit of length not area, and that he should write the equation out complete with units to ensure that his result comes out in units of area. So he writes:
[latex]6.2~\textrm{mi} \times 2.1~\textrm{mi} = 13.02~\textrm{mi}^2[/latex]
and the instructor nods approval but says, “and now we need the area in square kilometers”. Our downtrodden student proceeds to look up the conversion factor between miles and kilometers:
[latex]1 \textrm{mi} \simeq 1.609~\textrm{km}.[/latex]
Great. The calculator buttons click away until the student, exasperated, inquires “so the area in square km is [latex]13.02 \times 1.609[/latex], which equals about 20.95 right?”
The ever-patient instructor shakes her head: “there are 1.609 km in a mile, but how many square km in a square mile?”. Our student stares at the map and feigns interest in the question. On a whim, he asks “do I need to square the 1.609 too?” The instructor pats him on the shoulder and remarks “yep, write it all out, and don’t forget the units” as she walks away. Our student, relieved at having guessed correctly, writes:
[latex]6.2~\textrm{mi} \times 2.1~\textrm{mi} = 13.02~\textrm{mi}^2[/latex]
[latex]13.02~\textrm{mi}^2 \times \bigg(1.609 \frac{\textrm{km}}{\textrm{mi}}\bigg)^2 = 33.71~\textrm{km}^2[/latex]
To see why we need to square the conversion factor like our student ultimately did, let’s write out the conversion equation the way he did it at first, but using only the units (this is a variation of the dimensional homogeneity heuristic from Chapter 5):
[latex]\textrm{mi}^2 \times \frac{\textrm{km}}{\textrm{mi}} = \textrm{km}^2[/latex]
If we cancel common units, we should be able to show that the units of the left-hand side are equal to the units on the right-hand side, but here we can only cancel miles in the numerator from miles in the denominator on the left-hand side, leaving a meaningless unit equation: mi km=km2. That can’t be true.
If instead we reason that our conversion factor needs to allow us to cancel through to make the units equivalent on both sides, we square the conversion factor and its units to yield:
[latex]{mi}^2 \times \bigg(\frac{\textrm{km}}{\textrm{mi}}\bigg)^2 = \textrm{km}^2[/latex]
This approach can be generalized for other types of spatial unit conversions as well, provided that our original and desired units are not compound. Suppose we are measuring the size of something in units based on the length unit [latex]U_1[/latex] and we need to convert it into units based on the length unit [latex]U_2[/latex]. If the conversion factor between [latex]U_1[/latex]and [latex]U_2[/latex] is [latex]C_{1\rightarrow 2}[/latex], the conversion equation can be written:
[latex]U_{1}^d \times C_{1\rightarrow 2}^d = U_{2}^d \tag{9.1}[/latex]
In this equation, dd is the spatial dimensionality of the quantity, so its 1 for lengths, 2 for areas, and 3 for volumes. It’s important to note that the conversion factor [latex]C_{1\rightarrow 2}[/latex] should correspond to the number of unit 2’s per unit 1, as we did for the map area conversion above.
Note that unit conversion factors between compound units like acres and hectares are not subject to these concerns. There is no such thing as a square acre because an acre is already a unit of area, so nothing needs to be done to the conversion factor if you are converting from, for example, acres to hectares: there are 0.4047 hectares in an acre, period. In this way these compound units can make life easier, but if you are simultaneously working with other quantities in meters, this convenience comes at a price.
It might have occurred to you to approach the map problem in a slightly different way. Suppose that instead of computing the area in square miles immediately after measuring the sides of the rectangle, our student had converted the sides from miles to kilometers first. Does this make any difference?
In this case, the map distances are [latex]6.2 \times 1.609 = 9.976~\textrm{km}[/latex] and [latex]2.1 \times 1.609 = 3.379~\textrm{km}[/latex]. Their product is 33.71km2, which is the same result as before. That should come as no surprise, since the only difference is that the unit conversions from miles to km occurred before finding the area rather than after. Indeed this is one way to make the problem a bit simpler to think about, but thanks to the commutative property of multiplication there is no real difference between the approaches.
9.1.2 Scales and Scaling
The map scalebar in Figure 9.2 shows not only a graphical scale that can be used to directly measure real-world distances from the (scaled) map representation, but also indicates a ratio: 1:31,680. What does this scale mean? Does it have units?
Map scales are like most other dimensionless proportions, as we discussed in Chapter 5. The beauty of many dimensionless proportions is that we can use any units we want in them provided that both parts of the scale ratio or proportion have the same units. So for the map scale, we can say that 1 inch on the map is equal to 31,680 inches in the world that the map represents.[6] If we measure out a path on the map that is [latex]x[/latex] inch long, the distance we would cover walking along that path in the real world is [latex]x\times31680[/latex] inches. That’s not a very easy distance to envision because there aren’t any very familiar benchmarks near that quantity of inches, but we could convert the latter to feet or miles to make it simpler, and then we can re-express the scale in as a dimensional ratio:
31680 in. × 1ft./12in. = 2640 ft. We can go one step further still: 2640ft. × 1mi. / 5280ft. = 0.5mi. That works out pretty nicely, and it often does so by design! So we can restate the map scale as 1 inch = 0.5 miles, or equivalently 2 inches per mile. This means the same thing as the scale ratio 1:31,680 but is more specific because we have already chosen the units that we wish to measure with. Note that we cannot say that the map scale is 2:1 or 1:0.5 because in converting the second number from inches to miles we’ve made the scale statement unit-specific.
Maps aren’t the only thing that we encounter that are scaled representations of reality. When we are learning about microscopic properties of molecules or cells, we often look at diagrams or physical models of things that are too small to see. When looking through a microscope, we perceive a much enlarged version of the object of study. In each case, we are seeing representations of reality scaled to size that is easier for us to grasp. Importantly, we are also (usually) seeing things scaled isometrically, meaning that all dimensions are enlarged or shrunk by the same constant factor. We’ll see in later chapters some interesting problems associated with scaling that is not isometric.
9.1.3 Example: the area of roads in a county (Problem 4.3)
One reasonable sub-problem to address in the issue of deer-car collisions is how widespread are roads in the area of interest? As with several of the other teaser problems in this book, no specific county is cited, so as a first approximation I’ll just estimate numbers for my own home county: Story County, Iowa. According to Wikipedia, Story County has an area of 574 mi2. The extent of roads in Story County or elsewhere in the US is something that could be readily assessed with a GIS system, and that would certainly be among the most accurate and efficient ways to obtain this value for specific counties. However, for the sake of a first approximation let’s try something easier. Literature about road systems in the US suggests that there is about 1.2 miles of road per square mile of land, on average.[7] Clearly this is an underestimate in urban areas, and perhaps an overestimate in remote, rural areas. In the not-so-remote gridded farmscape of central Iowa (Figure 9.3), a road density closer to 2 mi./mi.2 is perhaps more appropriate. By this estimate, my county would have approximately 2×574=1148 miles of roads.
Road density is informative, but it only gets us partway to the notion of area. What we need to know now, given that we have road length, is the average width of a road. Let’s assume this is 20 feet. To be a meaningful area, we either need to decide to convert length to feet or width to miles.[8] Since the county area was estimated in miles, it would be wise for comparison purposes to convert road width into miles as well. Thus, the average road is about 20/5280=0.003788 miles wide. Multiplying that road width (in miles) by the total road length (in miles) yields about 4.35 square miles. That’s about [latex]4.35/574 \times 100\% = 0.76\%[/latex] of the county area!
9.2 Geometric Idealization or Approximation
Some problems require spatial measurements or computations that are complex, time-consuming, or difficult to visualize. In some of these cases, a rough estimate may be adequate for the type of solutions we seek; in other cases, we may wish to establish quick ballpark estimates before we dig too deeply into the complex computations, much like we just finished doing in the previous section. For these spatial problems, it can be helpful to idealize the spatial information we have in terms of simple geometric figures that we know something about. For example, suppose we wish to estimate roughly how much an 40cm-long snake might weigh, and we have no prior information or experience upon which to base this estimate. If we are able to estimate its diameter, we may make some progress by idealizing the snake as a long cylinder. Consulting the table below, we find that a cylinder’s volume is expressed as:
[latex]V = \pi r^2 h \tag{9.2}[/latex]
where r is half of the diameter and h is the length of the snake. If the largest r is around 1cm and h is 40cm, a first guess for the total volume is about 126 cm3. Now if this radius corresponds to the largest part of the snake, this volume might be an upper bound. Since the snake’s body tapers a bit, perhaps a mean radius is better – say 0.7cm. Now the volume is 61.6 cm3.
Next, given that many non-avian animals have densities close to that of water,[9] we can estimate the mass of the snake using density and volume. To see how we should do that, we might use a strategy described in an earlier chapter: write out the problem with just dimensions. We’re looking for how much it weighs, but really what we want is a mass. If we list the dimensions of the variables we have and want, they look like this:
[latex]\textrm{mass:} [M] \qquad \textrm{volume:} [L^3] \qquad \textrm{density:} [M~L^{-3}]\tag{9.3}[/latex]
we see that the mass we are looking to solve for appears in the density term. The volume term appears as a negative 3rd power in the density term and a positive 3rd power in the volume itself, so when multiplied together, volume (V) and density (ρ) should yield dimensions of mass: [latex]m = \rho V[/latex]. If we remind ourselves that the definition of density is indeed [latex]\rho = m/V[/latex], this makes sense as a simple algebraic modification of that definition. Thus, our estimated mass for the snake would be:
[latex]61.6 \textrm{cm}^3 \times 1.0 \textrm{g}/\textrm{cm}^3 = 61.6 \textrm{g}.\tag{9.4}[/latex]
Is this close enough? Perhaps, but that depends on the nature of the problem: why do we wish to know how much the snake weighs, and what will we do with that information?
9.2.1 Example: herbicide purchase (Problem 4.2)
We can use a similar approach to get a start with the herbicide volume needed to eliminate woody shrubs from our city greenspace. A reasonable assumption is that, when cut with a saw or lopper, the exposed stem cross-section of a woody plant is approximately circular. If the goal is to cover the stumps completely with a coating of herbicide, each stump will have a volume (from Equation 9.2) equal to its cross-sectional area [latex]\pi r^2[/latex] times the thickness h of the herbicide coating applied to the stump.
9.3 Measuring polygon area
Not all spatial bodies of interest to us are easily measured using the simple idealized shapes reviewed above. Alternatively, geometric idealizations introduce too much error for certain applications. Non-ideal shapes can, however, be approximated by irregular polygons in some settings. Here, we describe a method for computing the area of an arbitray two-dimensional polygon using a clever trick that is frequently built into CAD, GIS, and other geospatial software packages.
The trapezoidal algorithm primary requirement we must meet to use this method is to have coordinate pairs for each vertex in the polygon in a Cartesian (i.e., a plane with two orthogonal, linear axes; a.k.a. an x-y plane) coordinate system. This algorithm may be implemented easily enough by hand, but finding the area of a more complex shape is better left up to a computer. Let’s have a look at how this algorithm works.
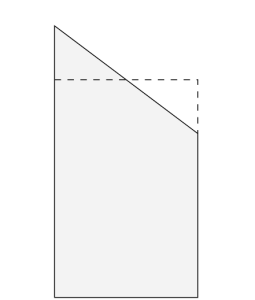
First, recall that a trapezoid is a four-sided shape in which only two sides are parallel, as in Figure 9.4. At first glance, it might seem that the area of the trapezoid would be challenging to estimate, but when we realize that it should be the same as the area of a rectangle that’s as tall as the average “height” of two vertical sizes of the trapezoid, we may see some hope.[10] We know that the area of a rectangle is just its height times its width: [latex]A_{\textrm{rect}}=hw[/latex]. For a trapezoid whose vertical sides have heights [latex]hl[/latex] and [latex]hr[/latex] for left side height and right side height, respectively, we can restate the formula for area in terms of the average of those heights:
[latex]\large{A_{\textrm{trap}}=\frac{1}{2}(h_l + h_r)w }\tag{9.5}[/latex]
Now suppose that instead of defining heights and widths in terms of [latex]h[/latex] and [latex]w[/latex], we have the vertices of our trapezoid in Cartesian coordinates.[11] Each point at a vertex (corner) of the trapezoid therefore has an [latex]x,y[/latex] coordinate, where [latex]x[/latex] refers to the horizontal coordinate direction and [latex]y[/latex] is vertical. In this system, note that the width of the trapezoid will be defined by the difference in two [latex]x[/latex] coordinates. So if we take the upper left corner in Figure 9.4 to have an [latex]x[/latex] coordinate of [latex]x_1[/latex] and the upper right corner to be at [latex]x_2[/latex], the width of the trapezoid is [latex]x_2 - x_1[/latex]. Similarly, if our trapezoid height extends to zero[12] in the [latex]y[/latex] coordinate direction, the “average” height of our trapezoid can be re-written by substituting [latex]y_1[/latex] and [latex]y_2[/latex] for [latex]h_l[/latex] and [latex]h_r[/latex]. If we make these changes to the area formula above, any given trapezoid in our coordinate system has an area:
[latex]A_{\textrm{trap}}=\frac{1}{2}(y_1 + y_2)(x_2 - x_1) \tag{9.6}[/latex]
Now consider the polygon depicted in Figure 9.4. Each pair of adjacent vertices can be viewed as the upper corners of a trapezoid. If we apply the formula above to each pair of adjacent vertices and add the areas together, what do we get?
[latex]A = \frac{1}{2}[(x_2 - x_1)(y_2 + y_1) + (x_3 - x_2)(y_3 + y_2) +... \\ ... + (x_1 - x_n)(y_1 + y_n) \tag{9.7}[/latex]
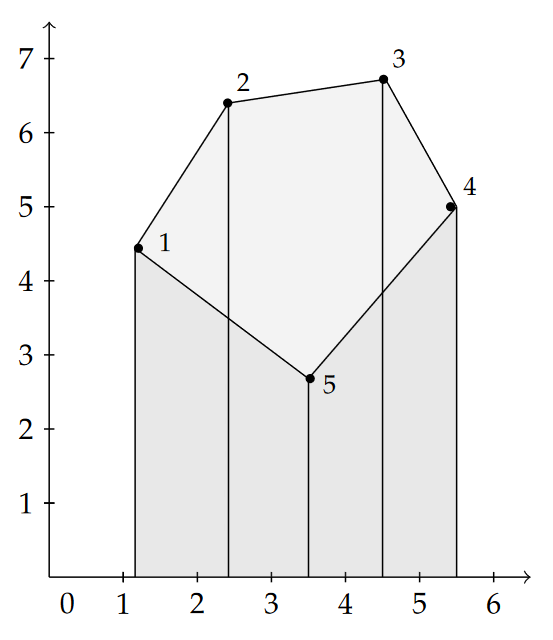
Here, [latex]n[/latex] is the number of vertices and the ellipsis “…” means that we’ve left out some number of terms in the equation, though in this case we’ve only got five vertices so we’ve only left out two terms. Notice that if we systematically label the vertices in our polygon in a clockwise manner, about half of the trapezoids will have negative areas and half will have positive areas, though the negative areas will be somewhat smaller. This is because as we come around the bottom of the polygon as we march clockwise from one pair of vertices to the next pair, our [latex]x[/latex] coordinates are becoming smaller as we go from right to left. This is good! The result is that the width value (and consequently the area) computes as negative, and as a result this lower trapezoid is subtracted from the total area of the polygon, which is exactly what we want! If we order the vertices counterclockwise we’d get the opposite result, but the resulting (negative) area would still be correct.
As mentioned earlier, this algorithm is readily implemented on a computer, using either spreadsheet software like Excel, or computational/statistical software like R. Likewise, this method is built into other software tools that natural resource students and professionals use, including most GIS packages.
9.3.1 Example: open-water waterfowl habitat (Problem 4.1)
One important variable that influences waterfowl abundance is the presence of different types of habitat. Most waterfowl feed extensively in open water, so the area of open wetland is a key habitat variable. In Section 9.3 we identified the trapezoidal algorithm as a tool for estimating the area of arbitrary shapes. We also acknowledged that, while it is possible to do the required computations by hand, automating the algorithm improves computational efficiency by orders of magnitude. The algorithm can be implemented as a formula in a spreadsheet containing the coordinates of the polygon but, as we’ve discussed, this operation is common enough that it is incorporated in most GIS software. Therefore, comparing watershed areas between the parcels described in Problem 4.1 is a geospatial problem. We nevertheless provide an opportunity in the chapter Exercises below to work with this algorithm directly.
Exercises
- What is the longest distance across the wetland in Figure 9.1?
- Estimate the dimensionless map scale ratio from the scalebar in Figure 9.1.
- Would the map scale be the same or different if you made an enlarged photocopy of a map?
- Use geometric approximation to estimate the area of the wetland in Figure 9.1.
- Use the trapezoidal algorithm to make a more precise estimate of the wetland area. The data below contains UTM coordinates of the wetland perimeter.
-
- Download the UTM coordinates data (XLS)
- For example, we can express all the quantities in terms of SI units of m, m2, and m3, or we can use more traditional U.S. agricultural units like feet, acres, and acre-feet. ↵
- One board-foot is equivalent to 144 cubic inches of merchantable timber; can be visualized as a 12 inch long and 12 inch wide board that is 1 inch thick. ↵
- Neither the acre nor the hectare need be any particular shape, nor do they necessarily need to be contiguous, though they usually are. ↵
- Perhaps this exercise is going the way of the paper map itself as people increasingly interact with only digital maps these days! ↵
- See the next section for more on scaling. ↵
- For better or worse, the US still persists with using inches, feet, and miles as conventional measures of distance in official maps and documents. Even though most scientists adopted the metric system long ago, we retain imperial units here to recognize the persistence of legacy units in our maps. ↵
- This number comes from: Transportation Research Board and National Research Council, 2005. Assessing and Managing the Ecological Impacts of Paved Roads. Washington, DC: The National Academies Press. https://doi.org/10.17226/11535. ↵
- This is a seemingly-trivial but still significant decision. In Schoenfeld’s framework for problem-solving, making this kind of decision deliberately with the broader goals and practical issues in mind is an example of control. ↵
- In so-called cgs units, the density of water is 1.0 g/cm3. ↵
- In Figure 9.4 you can imagine snipping the top of the trapezoid on the dashed line, flipping it over and filling the void in the upper right. Alternatively, we could imagine splitting the trapezoid into a shorter rectangle and a full-width triangle and compute the area as the sum of those two areas. With a bit of algebra, we find that the result is the same. ↵
- Cartesian just means that we are specifying the location of points in a two-dimensional coordinate system where the coordinate directions are perpendicular to one another. Note that the UTM coordinate system for maps is Cartesian, whereas latitude and longitude are not. ↵
- In fact, we could show that it needn’t go all the way to zero provided that all of the [latex]y[/latex] values in the trapezoid collection are positive all are negative, but this is left as an exercise. ↵

