Introduction
Introduction
Some Philosophical Notes
In a conventional math course, you might be confronted with a question like the following:
Find the roots of [latex]x[/latex] in the expression:
[latex]4x^2 - 13x + 6=0.[/latex]
You may be instructed or implicitly expected to apply an algorithm to this problem and provide the two possible roots. Most likely this would be an opportunity to use the trusty quadratic formula:
[latex]x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}[/latex]
If you weren’t already turned off, you might plug the values 4, -13, and 6 in for [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex] in the quadratic formula, perform some arithmetic and find the roots to be 0.56 and 2.69. Alternatively, if you’re like me, you’d let a computer program like Geogebra apply this algorithm, since that is what computers are for.
In any case, with these two roots in hand, you have an answer, isn’t that satisfying!? OK, maybe it is for some of you, but this has never been satisfying for me. No meaning was ever assigned to the variables or constants, nor was it claimed that the result had any context or significance. I don’t really know what to do with the answer, now that I have it. I’ve learned very little, except perhaps that I can enter the proper numbers into an algorithm. That is not to say that learning the algorithm is without value – indeed it is very valuable. But for most of us, the algorithm itself is not an end in itself, it is a means to an end. It is a useful tool that allows us a shortcut to a result when an equation presents itself in a quadratic form.
Though the problems in a conventional math class may look arbitrary, they are often designed to be “well-behaved”. You wouldn’t often see equations exactly like the example above, because the roots turn out to be icky decimal numbers rather than nice, clean integers. Furthermore, things get complex (literally!) if the numerical coefficients on the left-hand side of the equation are such that the term under the square-root in the quadratic formula turn out to be negative. Such a poorly-behaved case belongs to a completely different subject in the mathematics curriculum (complex analysis), and so cannot be imposed upon an unsuspecting algebra student. However, in the “real world”, there is no more reason to suspect a real result than a complex one, in those rare practical instances when one needs to find the roots of a second-order polynomial. Thus, in this approach we learn a very strict set of rules applicable only to an idealized subset of problems that may or may not have any significance outside of abstract trivia.
The approach we use in this course is to encounter math and statistics in the process of finding solutions to real—or at least plausible—problems in the natural sciences. Sometimes these real problems are messier than those out of a textbook. Often they will be open-ended and will require multiple steps and a variety of techniques. We’ll need to decide for ourselves what tools and techniques to use, according to the needs of the problem. Being creative in math classes isn’t what we’ve been trained to do, and at times it may be uncomfortable. That’s OK, we’ll take our time. But no matter the problem, we’ll always have a reason to be doing math or statistics – every quantity in an equation will have real meaning or role, and we can apply our non-quantitative knowledge and experience with these entities to help us solve our problems.
Let's have a look at the kind of problem that a natural resource manager or ecologist might care more about, a problem that we’ll return to periodically in this course. Consider the Iowa DNR’s estimates of the statewide pheasant population shown in Figure 1.1. Now consider the question that is important to many hunters and game managers around the state: what should we expect pheasant populations to look like in 5 years?
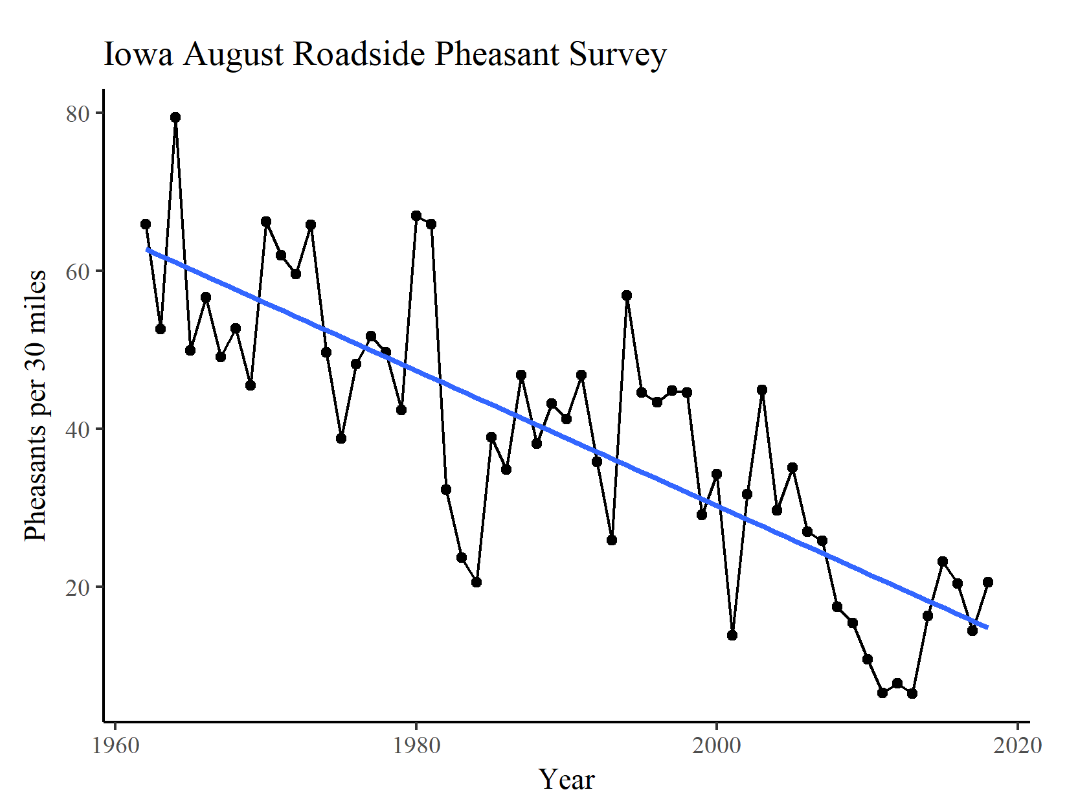
The black dots in the graph are annual results from roadside pheasants surveys, the dots are connected in chronological order with black lines,[1] and a blue line traces the long-term trend. In the roadside survey, DNR biologists travel 30-mile segments of rural roads on dewy late-summer mornings, count the pheasants observed in each stretch, and compile the data across the whole state.[2] The changes from year to year in this measure of pheasant population are similar to the changes in hunter harvest and are thought to be a good indication of the pheasant population as a whole.
| year | count |
| 2013 | 6.5 |
| 2014 | 16.3 |
| 2015 | 23.2 |
| 2016 | 20.4 |
| 2017 | 14.4 |
| 2018 | 20.2 |
| 2019 | 17.0 |
| 2020 | 20.0 |
| 2021 | 19.7 |
| 2022 | 19.6 |
The rebound in the roadside counts from 2013 to 2014 was characterized in the DNR report as a 151% increase, and the change from 2014 to 2015 was described as a 37% rise. The last few numerical value pairs plotted in the graph are also shown in Table 1.1 to the right.
This example may seem straight forward at first glance, and in some ways it is. The trend appears to indicate an overall decline in pheasant numbers across the state, and perhaps we should be prepared to take a more hands-on approach to managing pheasant numbers if we wish to sustain a viable game resource in the coming years. On the other hand, the year-to-year changes seem to be erratic, rising and falling in a way that seems to lack a pattern. Addressing the guiding question with any confidence, however, could be a bit challenging. If, for example, we were looking at the dataset at the end of 2011 following 6 straight years of steady decline, would we have been able to anticipate a rebound in 2014 or 2015? Probably not without a robust and reliable model of the factors that cause population changes and how those factors could change in subsequent years. These are advanced topics, but ones that wildlife managers have to incorporate into their management strategies in some situations.
On an even deeper level, the roadside pheasant count itself is a strange quantity that doesn’t exactly represent what we wish to know (i.e., the pheasant population). Instead, it is an easy-to-estimate approximation of the real population. As such, it is a sample from the larger population, at least one step removed from the quantity we seek. How does such a sample relate to the larger quantity we are after? That’s a pretty simple question in theory (i.e., in stats class), but when we account for the sampling methodology, timing, and observer variability, and we consider that pheasant visibility may not always be directly linked to population, it isn’t so straight-forward after all.
The observations we’ve made from this dataset are just some of the many complexities that we might uncover as we endeavor to solve problems in pheasant population or habitat management in Iowa. This example hints at the concepts of time series analysis, forecasting, and measurement uncertainty, as well as functional relationships between multiple variables and between samples and populations. Each of these concepts represents a quantitative tool that can be applied toward the larger problem-solving task. We’ll visit most of these concepts and many more en route to addressing practical problems and methods. But as we will see in the next chapter, the quantitative procedures that we employ in the problem-solving process are just a part of the arsenal necessary to solve practical problems. Furthermore, it should go without saying that some of the quantitative tools we do have at our disposal are not appropriate for some problems, and a key job of the problem-solver is to determine which tools those are. We’ll delve deeper into this issue a few pages ahead.

An ancient puzzler
“In a lake the bud of a water-lily was observed, one span above the water, and when moved by the gentle breeze, it sunk in the water at two cubits’ distance. Required the depth of the water.”
—Henry Wadsworth Longfellow
The lines above are from a poem in which a Mr. Churchill playfully challenges his wife with mathematical puzzlers. The problem he describes actually dates back many centuries, to a 12th-century Indian mathematician named Bhascara who posed the problem in verse in his book Lilavati.[3] As we look forward to learning the process of problem-solving, let’s imagine a dialogue between a student (S) confronted with this problem and a patient instructor (I). This isn’t quite the sort of problem we’re interested in really diving into, but the dialogue serves to illustrate a few points that we’ll address in the next chapter.
A problem-solving dialogue
S: Hmm, so lemme see if I understand this. Wait, is a span an actual distance? And a cubit?
I: Yes, they are old-fashioned and inexact measures of length. The cubit at least is about the length of a forearm, and people often take that to be about 18 inches. A span is from the tip of the thumb to the tip of your pinky if you stretch your hands out as far as possible, and that’s usually interpreted as 9 inches.
S: OK, so a span is 9 inches, so the water lily was 9 inches above the water at first. Then when the wind blows, the bud moves two cubits, so about 36 inches to one side until it is submerged. So we want to know how deep the water is. Umm...
I: Good start.
S: Well how am I supposed to... Hmmm... Alright, so would the depth just be 45 inches, I mean that’s 9 plus 36? No, that doesn’t make sense. Shoot... I’m not sure where to start?
I: Do you have a picture in your head of the situation you’re thinking about?
S: Yeah, sort of.
I: Do you think you could draw it?
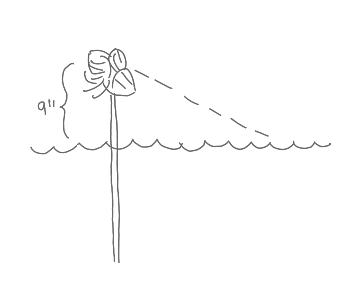
S: Um, I guess so... Yeah... here’s the lily bud 9 inches above the water when it’s standing straight up... Now when the wind blows it stretches to the side and then the bud is over here, 36 inches away. Wait, is that 36 inches to the right, or 36 inches from here to here [pointing from the upright bud to the bud at the waterline]?
I: I think you can assume 36 inches to the right, but that’s a really good question, and an important one to get sorted out before you get too far along. Did drawing the picture bring that question to mind?
S: Yeah, definitely. OK, so when the wind blows the lily over there, the stem is slanted like this... and ... so we want the depth of the water, which is this distance [drawing a dimension line from the lake bottom to the waterline]... so this makes a triangle, is that what I’m supposed to do?
I: There are no “supposed to’s” in this class.
S: Oh, so how will I know when I’m doing it right?
I: There’s more than one way to solve the problem, so there isn’t just one “right way”. If you’ve interpreted the problem correctly, chosen a solution procedure that doesn’t violate the fundamental principles of mathematics, and all your arithmetic is sound, you’ll get the correct answer and you’ll know it.
S: Oh. But... how do I know if I’ve got the right answer? You’re not going to tell me?
I: Welcome to the real world.
Exercises
- Make a list of the variables or factors that one might need to take into account when projecting future pheasant populations from historic data such as the Iowa Roadside Pheasant Survey.
- How do game wildlife managers benefit from making population estimates like the roadside survey?
- See if you can arrive at a solution for the Lilavati water lily problem. While you’re working on this, occasionally step back and think about what sorts of things you are doing to make progress. Are you trying to understand what the problem is about? Trying to appreciate the geometry? Trying to recall algorithms that relate different quantities in a geometric shape? If you feel stuck at any point, what do you think is preventing you from making progress? Record and annotate all of your thoughts and solution attempts, and try not to erase or scribble anything out.
- Note that connecting dots like this can imply continuity between data points, which may or may not be what we wish to indicate. ↵
- For more information on the pheasant population trends and the roadside survey method, consult the IDNR small game website. ↵
- One translation that can be readily found online is an 1817 translation by H.T. Colebrooke: Algebra, with Arithmetic and Mensuration, Brahmegupta and Bhascara, London, John Murray. ↵
A model in this context means an approximate mathematical representation of the real system from which predictions about the behavior of the real system may be made and tested.

