Part II. NUMERICAL REASONING
7. Reasoning with Data
This chapter summarizes some of the key concepts and relationships of single-variable statistics that we might find useful for characterizing measurements, particularly when we have measured a quantity at multiple times, or we’ve measured many individual members of a population or collection. This is not intended to be an exhaustive introduction to statistics, and does not in any way substitute for a proper statistics course. It does, however, point to some connections that we can make between the measurement and characterization of data and the scientific description of nature that we sometimes seek.
7.1 Measurement and Sampling
In the natural sciences we often need to estimate or measure a quantity or set of quantities that is too large, too numerous, or too complex to characterize completely in an efficient way. We can instead characterize it approximately with a representative sample. A representative sample is a small subset of the whole that is measured in order to characterize the whole.

Consider an example. In small headwater streams, many aspects of biotic health are linked with the size of the substrate – the sand, pebbles or boulders that compose the streambed. But it is impractical to measure all the gajillions of particles scattered over the entire bed. Instead, we attempt to get a smaller but representative sample of the bed material. This may be done in a number of different ways, but two common methods are: 1) to take one or more buckets full of sediment from the streambed and do a detailed particle-size analysis in a laboratory; and 2) measure the size of 100 randomly selected particles from the bed. Both methods obtain a sample, but each may represent the true streambed in a different way. The bucket method requires us to choose sample sites on the streambed. Our choices might be biased toward those places where sampling might be easier, the bed more visible, or the water shallower. In this case, our results might not be representative of the streambed as a whole.
The “pebble count” method, on the other hand, is intended to produce a more random sample of the streambed.[1] A person wading in the stream steps diagonally across the channel, and at each step places her index finger on the streambed immediately in front of the toe of her boot. The diameter of the particle that her finger touches first is measured, and then she repeats the process, zig-zagging across the channel until she has measured 100 (or some larger predetermined number) particles. In principle, this random sample is more representative of the streambed, particularly as the number of particles in the sample is increased. Of course, increasing the number of particles in the sample increases the time and effort used, but with diminishing returns for improving the accuracy of the sample.
Hypothetically-speaking, an alternative pebble-count method could be to stretch a tape measure across the stream and measure the particle size at regular intervals, say every half meter. We can call this strategy the “point count” method. This alternative is appealing since it ensures that samples are distributed evenly across the channel and that samples are not clustered in space. However, it is conceivable that such systematic sampling could lead to a systematic bias.[2] If for example the streambed had clusters or patterns of particles in it that had a wavelength of 0.5 m, you could be inadvertently sampling only a certain part of the top of each dune, which might skew your results toward particle sizes that are concentrated on dune crests. Thus, a random sample is usually preferable as it is less susceptible to this kind of systematic bias.
Quantities derived from a random sample are unrelated to one another in the same way that the size of one grain measured during a pebble count has no influence on the size of the next one. Part of our sequence of data might look like this:
12, 2, 5, 26, 4, 28, 19, 29, 3, 15, 31, 19, 24, 27, 7, 22, 28, 33, 21, 28, 13, 15, 25, 10, 14, 13, 16, 18, 33, 5
The random nature of this set of data allows us to use some of the familiar ways of describing our data, while boosting our confidence that we are also properly characterizing the larger system that we are sampling.
7.1.1 Example: mark-recapture
A frequent concern of the wildlife biologist is the abundance and health of a particular species of interest. Ideally, we could count and assess the health of every individual in a population, but that is usually not practical – heck, we have a tough enough time counting and assessing the health of all the humans in a small town! Instead of trying to track down every individual though, we can do a decent job by simply taking a random sample from the population and performing the desired analysis on that random sample. As we have seen, if we are sufficiently careful about avoiding bias in our sampling, we can be reasonably confident that our sample will tell us something useful (and not misleading) about the larger population that the sample came from.
If our concern is mainly with the population of a target species in a certain area, we can use a method called mark-recapture, or capture-recapture. The basic premise is simple: we capture some number of individuals in a population at one time, band, tag or mark them in such a way that they can be recognized later as individuals that were previously captured, then release them. Some time later, after these individuals have dispersed into the population as a whole, we capture another set. The proportion of the individuals in the second capture who are marked should, in theory, be the same as the proportion of the whole population that we marked to begin with. If the number of individuals we marked the first time around is N1, the number we captured the second time around is N2, and the number in the second group that bore marks from the first capture is M, the population P may be estimated most simply as:
[latex]\large{P=\frac{N_1 N_2}{M}}\tag{7.1}[/latex]
This comes from the assumption that our sample each time is random, and that the marked individuals have exactly the same likelihood of being in the second capture as they did in the first. Therefore, if we sampled and marked a fraction N1/P the first time around and sample N2 the second time around, then we should expect a fraction M/N2 of them to be marked.
Of course this whole plan can be foiled if some key assumptions are not met. For example, we need the population to be “closed” – that is, individuals do not enter and leave the population such that our sample is not coming from the same set of individuals each time. Problems could also ensue if our “random” sample isn’t random, if somehow the process of marking individuals either harmed them or made their likelihood of re-capture more or less likely, or if the time we allowed for them to re-mix with their population was not appropriate. On the last point, you can imagine that if we recapture tortoises 10 minutes after releasing them from their first capture, our second sample will not be very random. On the other hand, if we recapture marked fish 20 years after they were first marked, many of them may have died and been replaced by their offspring, and thus our assumption of a “closed” population is violated. So in planning a mark-recapture study, space and timescales need to be taken into account.
It is worth noting that the method described here is about the most stripped down version of mark-recapture. There are many modifications to the method and the equation used to compute population that either account for immigration/emigration, multiple recaptures, some possible re-recaptures, etc. There are also related methods using tagging and marking that can be used to explore the dispersal of individuals, migration routes and a lot more!
7.2 Describing measurements
Measurements, or “data”, can inform and influence much of a resource manager’s work objectives, since they convey information about the systems of interest. Sometimes the data speak for themselves: raw numbers are sufficiently clear and compelling that nothing more needs to be done to let the data speak. More commonly, however, the data need to be summarized and characterized through one or more processes of data processing and data reduction. Processing might simply refer to a routine set of algorithms applied to raw data to make it satisfy the objectives of the project or problem. Data reduction usually summarizes a large set of data with a smaller set of descriptive statistics. For a set of measurements of a simple quantity, for example, we might wish to know:
Things we often want to know about our data
- what is a typical observation?
- how diverse are the data?
- how should these properties of the data be characterized for different types of quantities?
The first point suggests the use of our measures of central tendency: mean, median and mode. The second goal relates to measures of spread or dispersion in the data. For example, how close are most values in the data set to the mean?
7.3 Central tendency
The central tendency of a data set is a characteristic central value that may be the mean, median, or mode. Which of these measures of central tendency best characterizes the data set depends on the nature of the data and what we wish to characterize about it.
Most of us are already familiar with the concept of a mean, or average value of a set of numbers. We normally just add together all of the observed values and divide by the number of values to get the mean. Actually, this is the arithmetic mean, and there are many alternative ways of computing different kinds of means that are useful in particular circumstances, but we won’t worry about these now. For our purposes, the arithmetic mean is the mean we mean when we say mean or average. It would be mean to say otherwise.
Before continuing, lets briefly discuss the different kinds of notation what we might use when talking about data. To define something like the mean with an equation, we’d like to make the definition as general as possible, i.e., applicable to all cases rather than just one. So we need notation that, for example, does not specify the number of data points in the data set but allows that to vary. If we want to find the mean (call it [latex]\bar{x}[/latex]) of a set of 6 data points (x1,x2, and so on), one correct formula might look like this:
[latex]\large{\bar{x} = \frac{x_1 + x_2 + x_3 + x_4 + x_5 + x_6}{6}}\tag{7.2}[/latex]
and of course this is correct. But we can’t use the same formula for a dataset that has 7 or 8 values, or anything other than 6 values. Furthermore, it is not very convenient to have to write out each term in the numerator if the data set is really large. So we need a shorthand that is both brief and not specific to a certain number of data points. One approach is to write:
[latex]\large{\bar{x} = \frac{x_1 + x_2 + ... + x_n}{n}}\tag{7.3}[/latex]
where we understand that n is the number of observations in the data set. The ellipsis in the numerator denotes all the missing values between x2x_2 and xnx_n, the last value to be included in the average. Using this type of equation to define the mean is much more general than the first example, and is more compact as long as there are 4 or more values to be averaged.
One additional way you might see the mean defined is using so-called “Sigma notation,”[3] where it looks like this:
[latex]\large{\bar{x} = \frac{1}{n}\sum\limits_{i=1}^n x_i} \tag{7.4}[/latex]
where the big [latex]\Sigma[/latex] is the summation symbol. If you’ve never encountered this before, here’s how to interpret it: the “summand”, the stuff after the [latex]\Sigma[/latex], is to be interpreted as a list of values (in this case xi) that need to be added together, and i starts at 1 and increases until you get to n. You can see the rules for what i means by looking at the text below and above the [latex]\Sigma[/latex]. Below, where it says i=1, that means that i begins with a value of 1 and increases with each added term until i=n, which is the last term. So in the end, you can interpret this to have a meaning identical to the equivalent expressions above, but in some cases this notation can be more compact and explicit. It also looks fancier and more intimidating, so people will sometimes use this notation to scare you off, even though it gives you the same result as the second equation above.
7.3.1 Mean versus Median
| species | weight (lbs.) |
|---|---|
| crappie | 0.5 |
| crappie | 0.5 |
| crappie | 0.5 |
| crappie | 0.5 |
| crappie | 0.5 |
| walleye | 0.75 |
| smallmouth | 1.0 |
| smallmouth | 1.0 |
| smallmouth | 1.0 |
| smallmouth | 1.0 |
| muskie | 16 |
| mean | 2.1 |
| median | 0.75 |
For some data sets, the mean can be a misleading way to describe the central tendency. If your creel after a day of fishing includes 5 half-pound crappies, a 3/4-pound walleye, 4 one-pound smallmouths and one 16-pound muskie (Table 7.1), it would be correct but misleading to say that the average size of the fish you caught was 2.1 pounds. The distribution of weights includes one distant outlier, the muskie, that greatly distorts the mean, but all of the other fish you caught weighed one pound or less. We might say in this case that the mean is sensitive to outliers.
The median is an alternative measure of central tendency that is not sensitive to outliers. It is simply the value for which half the observations are greater and half are smaller. From your fishing catch, the 0.75 pound walleye represents the median value, since 5 fish (the crappies) were smaller and 5 fish (the smallies and the muskie) were larger. The median may also be thought of as the middle value in a sorted list of values, although there is really only a distinct middle value when you have an odd number of observations. In the event that you’ve got an even number of observations, the median is halfway between the two middle observations.
7.3.2 Mode
The mode is the value or range of values that occurs most frequently in a data set. Since you caught 5 half-pound fish and fewer of every other weight value in the dataset, the mode of this distribution is 0.5 pounds. Now if the weights we’ve reported above are actually rounded from true measured weights that differ slightly, this definition becomes less satisfactory. For example, suppose the half-pound crappies actually weighed 0.46, 0.49, 0.5, 0.55 and 0.61 pounds. None of these are actually the same value, so can we say that this is still a mode? Indeed we can if we choose to discretize or bin these data. We might say that our fish weights fall into bins that range from 0.375 to 0.625, 0.625 to 0.875, 0.875 to 1.125, and so on. In this case, since all of our crappies fall in the range 0.375 to 0.625 (which is 5±1/8 lbs), this size range remains the mode of the data set. We can see this visually in a histogram, which is just a bar-chart showing how often measurements fall within each bin in a range (Figure 7.2).
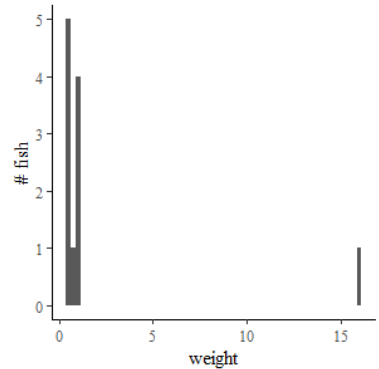
It is permissible to identify multiple modes in a data set if it improves the description. The first mode is the data bin that appears most frequently, but second and third and additional modes can be used as well. A second mode in our fish sample is in the 1-pound bin, which included 4 smallmouth bass. It is particularly useful in the case of multimodal data sets to report the modes because the multimodal nature of the data set cannot be represented by the mean or the median.[4] In fact, if you were only presented with the list of weights, you might still have a hunch that there were multiple species or multiple age-classes present in the creel due to the multimodal weights.
In practice, reporting all of these measures of central tendency may deliver the most complete picture of data, but as we’ve seen each is particularly useful in some cases and can be misleading in others. That said, we can actually infer additional properties of the dataset by noting, for example, the difference between the mean and median.
7.4 Spread
As mentioned previously, one way to quantify dispersion of a data set is to find the difference between any given observation and the expected value or sample mean. If we write this:
[latex]x_i - \bar{x}, \tag{7.5}[/latex]
we can call each such difference a residual. A residual could be used to describe the relationship between individual data points and the sample mean, but doesn’t by itself characterize the spread of the entire data set. But what if we add together all of these residuals and divide by the number of data points? Well, this should just give us zero, according to the definition of the mean! But suppose instead that we squared the residuals before adding them together. The formula would look like:
[latex]\frac{1}{n}\sum\limits_{i=1}^n (x_i - \bar{x})^2 \tag{7.6}[/latex]
This expression is defined as the variance and is strangely denoted by [latex]\sigma^2[/latex], but you’ll see why in a minute. Squaring the residuals made most of them larger and made negative residuals positive. It also accentuated those outlier data points that were farther from the mean. Now if we take the square root of the variance, we’re left with a finite positive value that very well represents how far data typically are from the mean: the standard deviation of the sample, or [latex]\sigma[/latex].[5] The formal definition of standard deviation looks like this:
[latex]\sigma = \sqrt{\frac{1}{n}\sum\limits_{i=1}^n (x_i - \bar{x})^2} \tag{7.7}[/latex]
The gives us a good sense for how far from the mean a typical measurement lies. We can now characterize a sample as having a mean value of [latex]\bar{x}[/latex] and standard deviation of [latex]\sigma[/latex], or saying that typical values are [latex]\bar{x} \pm \sigma[/latex]. But in reality, if we computed [latex]\bar{x}[/latex] and [latex]\sigma[/latex], the bounds set by [latex]\bar{x} - \sigma[/latex] and [latex]\bar{x} + \sigma[/latex] only contain about 68% of the data points. If we want to include more of the data, we could use two standard deviations above and below the mean, in which case we’ve bounded more than 95% of the data.
7.5 Error & Uncertainty
One piece of information we have thus far omitted from our list of properties that fully define a quantity’s value is uncertainty. This is particularly important when we are quantifying something that has been measured directly or derived from measurements. Thus, to even more completely define the value of a measured quantity, we should include some estimate of the uncertainty associated with the number assigned to it. This will often look like:
[latex]x = x_{best} \pm \delta x, \tag{7.8}[/latex]
where x is the thing we are trying to quantify, xbest is our best guess of its value, and [latex]\delta x[/latex] is our estimate of the uncertainty.
Though it will depend on the quantity in question, our best estimate will often be the result of a single measurement or—better yet—the mean of a number of repeated measurements.
7.5.1 Uncertainty in measured quantities
All measurements are subject to some degree of uncertainty, arising from the limited resolution of the instrument or scale used to make the measurement, or from random or systematic errors resulting from the method or circumstances of measurement. Let’s consider an example:
Suppose two fisheries biologists each measured the lengths of ten of the brook trout captured during the electrofishing traverse from Problem 4.7. Both used boards with identical scales printed on them, graduated to half of a centimeter. They then plan to put their measurements together to get a data set of 20 fish. One of them was trained to pinch together the tail fins to make this measurement, while the other was not. In addition, because they wished not to harm the fish, they made their measurements quickly, even if the fish flopped and wiggled during the measurement. What are the potential sources of error and how big are they relative to one another?
For starters, implicit in the graduations on this board is that the user cannot confidently read any better than half-centimeters off the scale. He or she can, however, visually interpolate between two adjacent graduations to improve precision (see below). However, this step is inherently subjective and limits the certainty of the measurement. We might call this instrumental error because its magnitude is set by the instrument or device use to make the measurement. One way to reduce this source of error is to use a more finely-graduated scale.
A second source of error arises from the hasty measurements and the fact that the fish were not necessarily cooperative. Perhaps the mouth was sometimes not pressed up all the way against the stop, or the fish wasn’t well aligned with the scale. Some lengths may have been too large or small as a result, yielding a source of error that was essentially random. Indeed, we can call this random error since its sign and magnitude are largely unrelated from one measurement to the next.
Reducing this source of error in this case would require either more careful and deliberate effort at aligning and immobilizing the fish, or making multiple measurements of the same fish. Both of these solutions could endanger the fish and may therefore not be desirable.
A third source of error is associated with the difference in the way the two scientists dealt with the tail fin. Length measurements made with the fins pinched together will usually be longer than those without. Had they measured the same group of ten fish, one set of measurements would have yielded lengths consistently smaller than the other. This is a systematic error, and can often be troublesome and difficult to detect. This highlights the need for a procedural statement that establishes clear guidelines for measurements wherever such sources of systematic error can arise.
Each of these types of error can affect the results of the measurements, and should be quantified and included in the description of the best estimate of fish length. But errors can affect the best estimate in different ways. Instrumental error, as described above, can itself either be random or systematic. The printed scale on one of the fish measurement boards could be stretched by a factor of 3% compared to the other, resulting in a systematic error. Likewise, one board might be made from plastic that is more slippery than the other and thus more difficult to align the fish on. This could result in additional random error associated with that device. But what are the relationships between these types of errors and the best estimate that we are seeking?
Error or variation? Questions to ask yourself
- What were possible sources of error in your measurements? Are they random or systematic?
- How can you tell the difference between error in measurement and natural variability?
7.5.2 Real variability
Not all deviations from the mean are errors. For real quantities in nature, there is no good reason to assume that, for example, all age-0 brook trout will be the same length. Indeed we expect that there are real variations among fish of a single age cohort due to differences in genetics, feeding patterns, and other real factors. If we’re measuring a group of age-0 fish to get a handle on how those fish vary in size, then at least some of the variation in our data reflects real variation in the length of those fish. How do we tease out the variation that is due to errors from the variation that is due to real variability?
Often a good approach is to try to independently estimate the magnitude of the measurement errors. If those measurement errors are about the same magnitude as the variations (residuals) within the data, then it may not be possible to identify real variability. However, in the more likely event that our measurements are reasonably accurate and have small measurement errors compared to their spread about the mean, then the indicated variations probably reflect true variability.
This observation returns us to our earlier question: when we seek to characterize some quantity how should we identify our best estimate and our degree of uncertainty in that estimate. If we wish to characterize a single quantity and our certainty that our best estimate is close to or equal to the true value, we should use the mean of repeated measurements of this value and the standard error of those measurements. The standard error can be readily estimated by dividing the standard deviation of the repeated measures by the number of measurements n:
[latex]SE=σn.\textrm{SE} = \frac{\sigma}{\sqrt{n}}. \tag{7.9}[/latex]
This should be equivalent to the standard deviation of a number of estimates of the mean [latex]\bar{x}[/latex], if several samples were taken from the full population of measurements. Like the standard deviation, we can be about about 68% confident that the range xbest+SE to xbest – SE includes the true value we wish to characterize, but if we use 1.96 SE instead, we can have 95% confidence.[6] A complete statement, then, of our best estimate with 95% certainty in this context is to say:
[latex]x = x_{best} \pm 1.96~\textrm{SE}, \tag{7.10}[/latex]
If instead we desire a characterization of a typical value and range for something that has real variability among individuals in a population, we will usually describe it with the mean and standard deviation.
[latex]x_{best} \pm 1.96~\sigma \tag{7.11}[/latex]
7.6 Distributions
The kind of data we’ve been talking about thus far is univariate: a single quantity with variable values like the diameter of a stream-bed particle, or the length of a fish. As we know, not all age-0 brook trout are the same size. In a first-pass capture of 50 fish, for example, we should expect some variability in length that might reflect age, genetics, social structure, or any other factor that might influence development. The variation may be visualized graphically in a number of ways. We’ll start with a histogram.
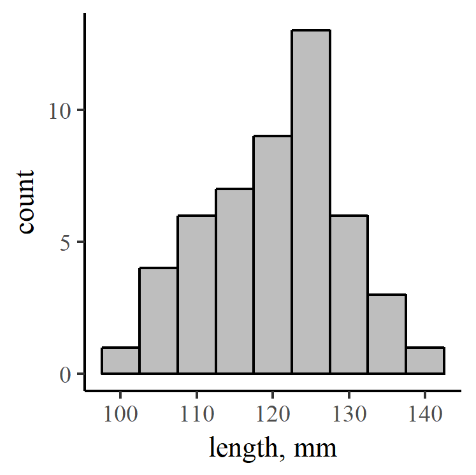
A histogram shows the distribution of a set of discrete measurements – that is the range of values and the number of data points falling into each of a number of bins, which are just ranges of values (112.5 to 117.5 is one bin, 117.5 to 122.5 another…). This can be called a frequency distribution, and a histogram is one of the best ways to visualize a frequency distribution (Figure 7.3).
But what if we had uniformly distributed data? A uniform distribution means that it is equally likely that we’ll find an individual with a length on the low end (97.5-102.5 mm) of the range as any other. That would look quite different – there would be no hump in the middle of the histogram, but rather a similar number of measurements of each possible length. The uniform distribution is great: in fact, we count on uniformity sometimes. If you are at the casino and rolling the dice, you probably assume (unless you’re dishonest) that there is an equal probability that you’ll roll a 6 as there is that you’ll roll a 1 on any given die. We can call that a uniform probability distribution for a single roll of a die. But What if the game you are playing counts the sum of the numbers on 5 dice? Is there still a uniform probability of getting any total value from 5 to 30?
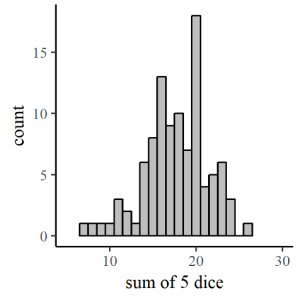
We could actually simulate that pretty easily by randomly choosing (with a computer program like R[7] or Excel) five integers between 1 and 6 and adding them together. Figure 7.4 shows the plot that comes out. Looks sorta like a bell curve, right? Well, how likely is it that you’ll get five 1’s or five 6’s? Not very, right? You’re no more likely to get one each of 1,2,3,4 and 5 either, right? However, there are multiple ways to get a 1,2,3,4 and 5 with different dice showing each of the possible numbers, whereas there is only one way to get all sixes and one way to get all ones. So there are better chances that you’ll get a random assortment of numbers, some higher and some lower, and their sum will tend toward a central value, the mean of the possible values. So, since your collection of rolls of the dice represent a random sample from a uniform distribution, the sum of several rolls will be normally distributed.
What’s it got to do with fish? If we sample brook trout randomly from one stream reach and measure their lengths, we might expect them to be normally distributed. Describing such a normal distribution with quantities like the mean and standard deviation gives us the power to compare different populations, or to decide whether some individuals are outliers. The nuts and bolts of those comparisons depend on how the type of distribution represented by the population. An ideal normal distribution is defined by this equation:
[latex]f(x) =\frac{1}{\sqrt{2\pi \sigma}}\exp\bigg[\frac{(x-\mu)^2}{2\sigma^2}\bigg] \tag{7.12}[/latex]
and it’s graph, in the context of our original hypothetical distribution of fish lengths, looks like the red line in Figure7.5.
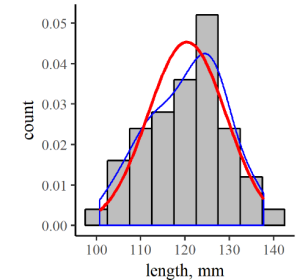
In order to compare the continuous and discrete distributions, we’ve divided the counts in each bin by the total number in the sample (50), to yield a density distribution. The blue line is just a smoothed interpolation of the top centers of each bar in the discrete distribution, so it generally reflects the density of data within each bin. As you can see, the discrete distribution density and the continuous normal distribution functions are similar, but there are some bumps in the discrete distribution that don’t quite match the continuous curve. As you can imagine though, that difference would become less pronounced as your dataset grows larger. Related to this, then, is the idea that your confidence in the central tendency and spread derived from your dataset should get better with more data.
Exercises
- Download the data from Derek Ogle’s InchLake2 dataset from the fishR data website. Using either a spreadsheet or data analysis package, isolate the bluegill from the dataset and identify the following:
- Mean bluegill length.
- Standard deviation of bluegill length.
- Mean bluegill weight.
- Standard deviation of bluegill weight.
- The graph and data table below and right show measurements of brook trout lengths from pass #1 of the electrofishing campaign described in Problem 4.7. Use these resources to answer the following questions:
- Judging from the histogram in Figure 7.6, does the dataset contain just one mode or more than one? What might be the reason for this?
- What is the mean and standard-deviation for the (presumed) age-0 portion of this sample?
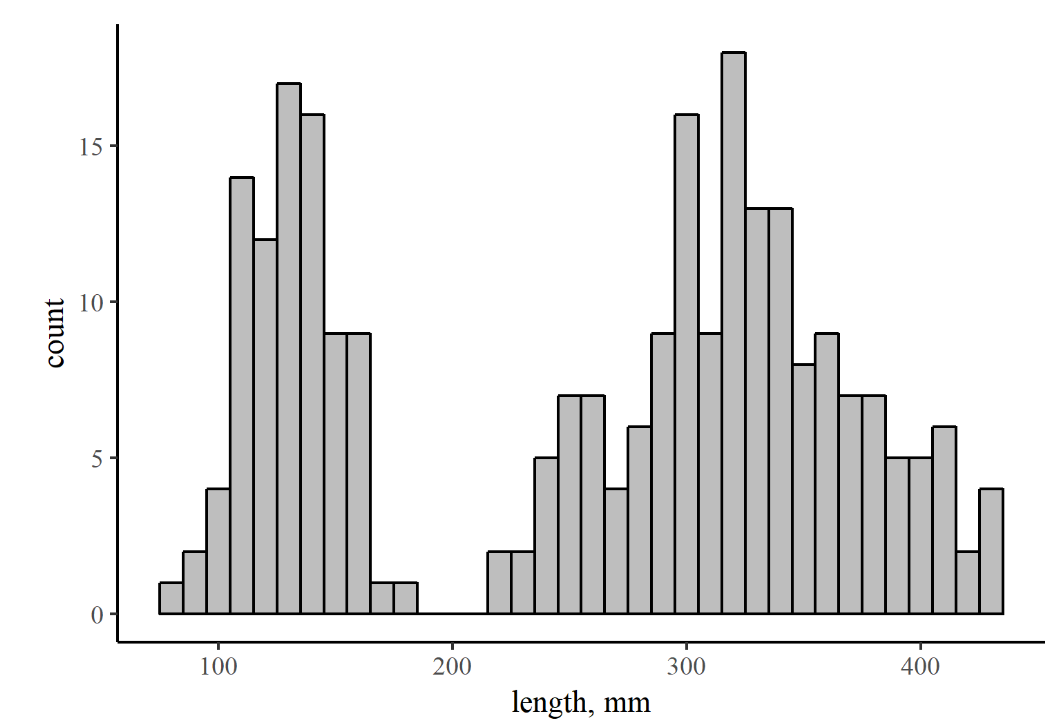
- Download the Brook trout length data [XLS] (all lengths in mm)
- This method is sometimes called the “Wolman pebble count” method for Reds Wolman, the scientist who first described and popularized it. ↵
- Systematic sampling is sometimes an easier, more straight-forward approach to sampling. However, if the setting within which sampling is taking place might have some systematic structure, systematic sampling could inadvertently bias the sample. ↵
- This symbol is a handy shorthand for the process of adding a bunch of quantities together, but also serves the purpose of scaring many poor students away. Once you realize that it’s just an abbreviation for listing all the the terms to be added (x1 + x2 + ...) and some of the rules for doing so, it becomes a tad less fearsome. ↵
- In some cases, multi-modal data can be suggestive of a mixed sample; that is, there is more than just one type of thing or from more than just one source in the sample. ↵
- If you keep track of the units of these different measures of spread, you’ll notice that the standard deviation should have the same units that the original data, xi does. ↵
- Note that we are currently assuming that our measurements are normally distributed. ↵
- R is a top choice software for general-purpose data analysis and modeling. It is free software, works on most computer platforms, and has nearly infinite capabilities due to the user-contributed package repository. Learn more about R at https://cran.r-project.org/ ↵
Instrumental error is fixed by the resolution of the device used to make a measurement, and can usually only be reduced by using a more precise instrument.
Systematic errors result in data that deviate systematically from the true values. These errors may often be more difficult to detect and correct, and data collection efforts should make great pains to eliminate any sources of systematic error.

