Part III. SPATIAL REASONING
10. Triangles
10.1 Measuring with Triangles
It is fair to ask why we should bother learning about triangles, since their relevance to ecology and natural resources isn’t immediately apparent. Indeed, natural materials tend to approximate more tabular or rounded shapes, and true triangles are harder to find in nature by comparison. But the real power of triangles is not in where we can see them, but where we can imagine them.
Believe it or not, imaginary triangles can help us measure properties of a landscape or organism, and that fact is firmly incorporated into many of the tools and technologies that researchers and professionals use. In particular, the ratios between the lengths of triangle sides is one of their key assets. In this chapter, we’ll review some of the properties of triangles and see how these properties can be leveraged to measure things we care about.
10.2 Trigonometry primer
Trigonometry is the study of triangles, specifically the relationships between the lengths of their sides and the angles between them. At first glance, that might not seem like it is very relevant to the natural sciences, but a few examples might convince you otherwise:
- Determining the distance “as the crow flies” between two geographic points is often most easily done with the help of triangles.
- Measuring the height of a tree or a mountain can employ triangles.
- Telemetry often uses triangulation to determine the geographic location of collared animals.
If you’ve had a trigonometry class, you might associate the discipline with manipulating equations with [latex]\sec 2\theta[/latex] and [latex]\cot(1+\pi/2)[/latex]. Outside of math class, did you ever find yourself needing to find the secant of an angle? Not likely. But it isn’t too uncommon to encounter the likes of sine and cosine, which are often written sin\sin and cos\cos, respectively. That’s because they are really, really useful.[1] And it turns out, nearly all the other trig functions you may have learned about are readily defined using sines and cosines! For example, the tangent of an angle can be defined as the ratio of the angle’s sine to its cosine, but it is so useful that we should recognize it as well.
As far as I’m concerned, on the off chance that you ever need to manipulate an equation containing the hyperbolic cosine (cosh\cosh) of something, you can look it up or type it into an internet tool like Wolfram|Alpha.
If this is your first experience with trigonometry, have no fear, we’ll take it slow!
Similarity
Similarity is a concept that may not boast enough sophistication to warrant its inclusion in a trigonometry class. However, it is an intuitively easy idea to grasp and its utility can be great. And fortunately for modern scientists, the formal application of similarity allows us to design tools for measuring things efficiently in the field.
The principle of geometric similarity[2] is straight-forward. If we have a given shape with known side lengths and/or known angles formed between the sides, we can say that another shape is similar if it has the same number of sides and a relationship between those sides and angles that is the same as our reference shape. The two shapes can still be similar even if they are not the same size or orientation. If any combination of translation (moving the shape), rotation, reflection (a mirror image), or isometric scaling could allow you to overlay one shape on the other to find them to be identical, the shapes are similar.
For triangles, the qualifying criteria for similarity are simple, since there are only three sides and one internal angle at each of the three vertices. For shorthand, when two triangles have one angle that is identical, we’ll call that A. When two triangles have all three angles equal, we’ll refer to that is AAA. Likewise, if the side-length of one side of two triangles is equal, we’ll describe that with S. With these definitions, we’ll make the following claims, as yet unproven, about the criteria for determining similarity:
Triangle Similarity
Two triangles are similar if any one of the following can be established:
- AAA. The angles of one triangle are equal to the angles of the second.
- SSS. The side-lengths of one triangle are equal to those of the second. Side lengths may be scaled by a constant CC if that constant is the same for each side.
- SAS. Two side-lengths and one angle of one triangle are equal to those of the second. Side lengths may be scaled by a constant CC if that constant is the same for each side.
When you’ve reached the end of this chapter, you should be able to show how each of these criteria for similarity could be derived from one of the others. That is left as an exercise for you to work on, one that can build your intuition for using triangle properties for problem solving.
10.2.1 The right triangle and sohcahtoa
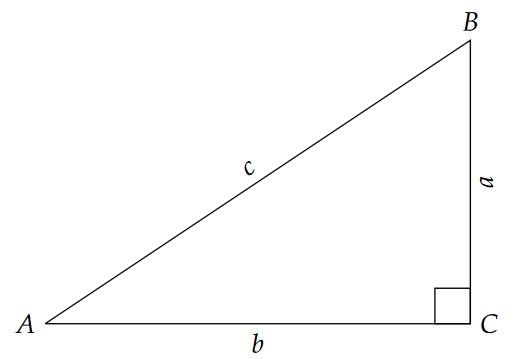
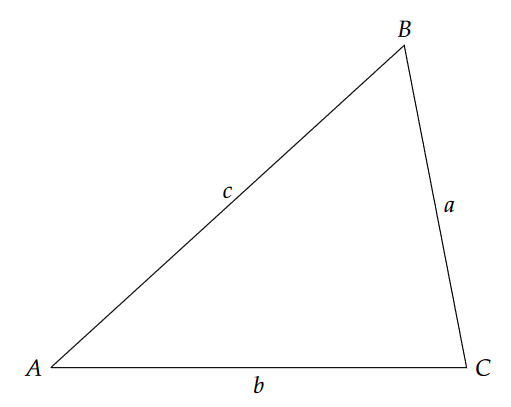
The mnemonic SOHCAHTOA is one of a small number of things that most trig students remember years after taking the class. Indeed this is really helpful way to remember the algorithms relating the basic trig functions to ratios between the sides of a right triangle. But it reveals nothing about the ways that triangles can be employed for practical purposes. So before we deal with these functions, let’s revisit what a right triangle is, where we might encounter one, and a few terms and rules regarding these beasts. Figure 10.2 shows a nice, well-behaved one.
Notice that each vertex (a corner point) joins two of the three sides and doesn’t touch the side that is opposite it. For reasons that might be apparent in a moment, we choose names for the sides and vertices that imply a relationship between a vertex and the side opposite it. So for example, side a is opposite vertex A (meaning the vertex A is not one of the endpoints of side a). It probably satisfies your intuition that the size of the angle at a vertex might have some simple relationships to the length of its opposite side – at least there is a more intuitive relationship there than between vertex A and one of the other two sides. Imagine keeping vertices A and C stationary, but allowing the angle at A to grow. It is plain to see that if the angle [latex]\angle A[/latex] increases, the vertex B must move up and the length of side a increases accordingly. This thought experiment produces similar results for the other opposing side/angle pairs as well, and we’ll use it to our advantage shortly in dealing with triangulation.
One of the most fundamental properties of all triangles is that the three vertex angles sum to 180°:
[latex]\angle A + \angle B + \angle C = 180^{\circ}[/latex].
For the special case of a right triangle, the right angle by definition is 90°, so the other two angles must be smaller than 90°. This seems obvious, but it has an important consequence: the longest side of a triangle is the one that is opposite the largest angle. Therefore, since the right angle is the largest angle in a right triangle, the longest side (which we call the hypotenuse) is across from the right angle (Figure 10.3).
In addition to the rule that angles must sum to 180°, one of the most powerful properties of right triangles is their adherence to the Pythagorean theorem:
[latex]a^2 + b^2 = c^2. \tag{10.1}[/latex]
This is always true provided that cc is the hypotenuse of a right triangle. It turns out that there is a simple modification that can be made to this if we are dealing with any arbitrary triangle. But before we go much farther, consider an example setting where a right triangle can be a useful aid to measurement.
Example: overland distances
If you are visiting GPS waypoints stored as UTM coordinates, the distance on-the-ground between two points might not be obvious from the coordinate sets. For example, what is the distance between (452632452632,46602144660214) and (452991452991,46605804660580), the marked locations of two observed dickcissel nests? Once we recognize these ordered pairs as the geographical equivalent of (x,y) pairs, it is pretty easy to see that the second nest is 452991−452632=359 m east and 4660580−4660214=366 m north of the first.
But neither a dickcissel nor an ornithologist would likely go from one nest to another by first going 366 m north and then 359 m east. Both would be more likely to go in an approximately straight line. Since east and north are perpendicular, we can construct a triangle like Figure 10.4, with a 359 m long easting side and a 366 m long northing side to represent the coordinate distances. The as-the-crow-flies distance is the hypotenuse of the triangle since it is opposite the right angle. Therefore we can use the Pythagorean theorem to find that distance, which we can call dd:
[latex]d^2 = (\textrm{easting})^2 + (\textrm{northing})^2 \tag{10.2}[/latex]
[latex]d = \sqrt{(\textrm{easting})^2 + (\textrm{northing})^2} \tag{10.3}[/latex]
[latex]d = \sqrt{(359~m)^2 + (366~m)^2} = 513~\textrm{m} \tag{10.4}[/latex]
North is toward the top of the page.
Knowing that the second nest is about 513 m away from the first is great. But if you were to give instructions to a field assistant to walk 513 m from the first nest to find the second nest, that alone is insufficient information to get to the correct place. Which direction does she have to go? You could, of course, simply have her walk north 366 m and then east 359 m, but that wouldn’t be terribly efficient. What is missing is obviously the direction. If she’s carrying a compass, you could give her a bearing or compass direction to follow, but what is that bearing, and do we have enough information to determine it?
10.2.3 Angles and azimuths
At this point, we need to draw more important distinctions regarding coordinate systems and conventions. When we need to be more accurate than simply saying “northeast”, compass bearings are often given as angles in degrees. Some people prefer to use quadrant bearings, where directions are given with respect to deviations from north or south. For example, due northeast might be expressed as “north 45 east”, or equivalently N45°E. That can be interpreted as 45° east of due north. Similarly, southeast could be S45°E and southwest is S45°W. This can sometimes be easier to understand in conversation, but bearings expressed in azimuth are less prone to misinterpretation. Azimuth is the compass direction in degrees clockwise from north, increasing continuously from 0° to 360°. In this system, north is both 0° and 360°, east is 90°, south is 180° and west is 270° (Figure 10.5).
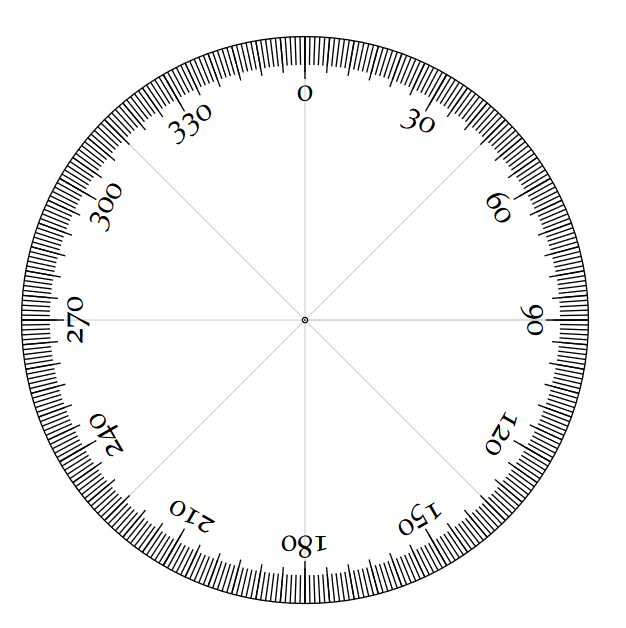
In the world of mathematics, angles are usually measured counterclockwise from the x-axis.[3] Not only does this mean that the starting point (0°) is in a different place, but it increases in a different direction. We will occasionally employ this convention, since it is so prevalent in quantitative topics unrelated to geography. But for the current problem, we’ll stick with azimuth.
Returning to the problem of finding the dickcissel nest, how can we decide what bearing to give to the field assistant? Since the easting and northing distances are similar, we can be fairly confident that it will be near 45º (NE), but probably not exactly that. But how do you determine the unknown angles in a triangle when you only know one angle (the right angle) and all of the side lengths? Aha! sine and cosine to the rescue!!
10.3 Angles, circles and sines

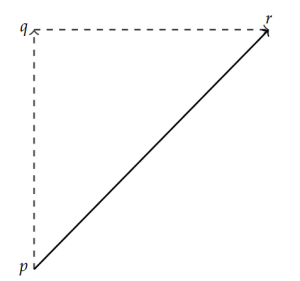
inside the unit circle.
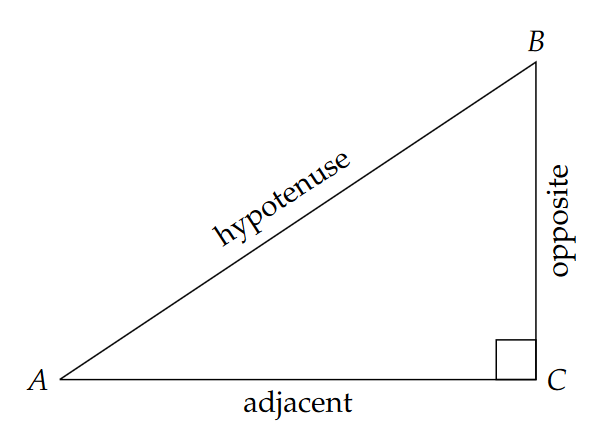
Before we proceed with finding the azimuth, let’s more formally define a few trigonometric quantities. We’ll do this initially in a mathematics framework, using an x-y coordinate system with angles increasing counterclockwise from the x-axis. Figure 10.6 shows what we might call the “unit circle”, a circle centered on the point (0,0) (also called the “origin”) with a radius of 1 unit. If we choose any point on the circle, call it p, it lies a distance of 1 unit from the origin. But its coordinates are not immediately obvious. As with the case of the dickcissel nests, however, we can break the path from the origin to p into a component in the x direction and a component in the y direction. Connecting each of those component paths with the direct path (the radius line), we end up with a right triangle [latex]\triangle \text{OAH}[/latex], as illustrated in yellow in Figure 10.6.
Since we have a right triangle, we could use the Pythagorean theorem again to find an unknown side length, provided that we know two of the sides. But in this case, we do not know two sides. Instead we know the angle [latex]\theta[/latex] between the x-axis and the line connecting the origin with point p. We also know that this line, call it H for hypotenuse, has length 1 by definition. The other two sides, O and A for opposite and adjacent, are unknown but can be found from the fundamental trigonometric functions.
Trigonometric Ratios
- The sine of an angle is the ratio of the length of the opposite side (OO) to the length of the hypotenuse side (HH).
- The cosine of an angle is the ratio of the length of the adjacent side (AA) to the length of the hypotenuse side (HH).
- The tangent of an angle is the ratio of the length of the opposite side (OO) to the length of the adjacent side (AA).
The tangent is identical to the ratio of the sine to cosine of an angle, which you can see is equivalent to the above definition if you cancel the hypotenuse terms in the ratio of ratios. These are loaded definitions, so let’s take a few moments to ponder what we’ve just seen.
- The trig functions are functions in the formal sense: they convert an input (angle) to a unique output (ratio of side lengths).
- The opposite and adjacent sides are defined relative to the angle that is the argument of the trig function.
- The output of each trig function is a dimensionless quantity that represents the ratio of two side lengths.
- If we know one angle (other than the right angle) and one side length, we can find the two remaining side lengths using the trigonometric functions.
In equations, we don’t spell the full name of these functions, but instead use sin, cos, and tan as shorthand. With this shorthand and the definitions above, we can construct a few simple equations that can help us find the unknown side lengths O and A in Figure 10.6:
[latex]\sin{\theta}=\frac{O}{H} \tag{10.5}[/latex]
[latex]\cos{\theta}=\frac{A}{H}\tag{10.6}[/latex]
Since we know [latex]\theta[/latex] and H on the unit circle, we can rearrange these equations to solve for the unknowns. Multiplying both sides of each equation by H, we get:
[latex]H\sin{\theta}=O \tag{10.7}[/latex]
[latex]H\cos{\theta}=A \tag{10.8}[/latex]
Now the reason we have done this in the unit circle is that H=1, so we essentially end with the definitions [latex]\sin\theta=O[/latex] and [latex]\cos\theta=A[/latex]. An important thing to realize, then, is that we can scale up to any arbitrary side lengths. Suppose we were interested in not a triangle with hypotenuse 1 unit, but one with hypotenuse 55 meters. Defining f=55 and isometrically scaling all the triangle sides by that factor, we can see for example that:
[latex]\sin{\theta}=\frac{fO}{fH} \bigg[\frac{\textrm{m}}{\textrm{m}}\bigg] \tag{10.9}[/latex]
Of course the f’s simply lengthen H and O by the same common factor, and could be easily canceled. But this illustrates the fact that sine and other trig functions describe dimensionless side-length ratios, and that those ratios can scale proportionally without changing the sine, cosine, and tangent of the angles! An obvious implication is that if one vertex of a right triangle has the same cosine and sine as another triangle, the triangles can be shown to be similar.
Actually, we already knew that, since by knowing one angle other than the right angle in a right triangle we can easily find the third. Recall, then, that one of the criteria for identifying similarity in triangles is AAA, or equality of all three angles regardless of side length. For any pair of similar right triangles, the only difference in side lengths is a constant scaling factor f. Thus, any right triangle can be scaled down to a similar one on the unit circle by dividing all side lengths by the length of the hypotenuse, so that H/f = 1!
In addition to simplifying triangle scaling, the unit circle also allows us to imagine moving point pp along the perimeter and observing how the lengths of A and O change accordingly. In fact, the software Geogebra is perfectly suited for doing this, and I highly recommend playing around with it to boost your intuition. The key thing to notice is that the denominator of the side ratios defined as the sine and cosine is the hypotenuse, or 1 on the unit circle. So the lengths of the opposite (sine) and adjacent (cosine) sides are the output of those respective functions. For angles between 0° and 90°, both functions range from 0 to 1. If you allow x and y to take on negative values as point p goes down or to the left of the origin, you’ll see that both functions remain between -1 and 1, inclusive.
But tangent is a different story. Recall that one definition for the tangent of an angle is O/A. You can see that for a small angle [latex]\theta[/latex], O is quite small and A is pretty close to 1, so the ratio of the two will be nearly 0. O and A are equal and [latex]\tan\theta=1[/latex] when [latex]\theta[/latex] is 45°, and as [latex]\theta[/latex] approaches 90°, A approaches 0 and O approaches infinity, so [latex]\tan\theta[/latex] approaches infinity as well. What do you suppose happens as [latex]\theta[/latex] gets larger than 90°?
10.3.1 Example: tree clinometry
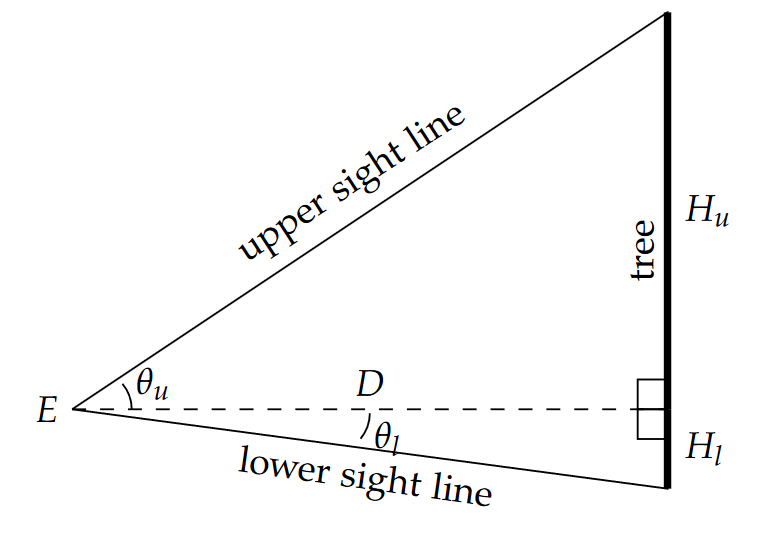
One of the most common ways to measure the height of a tree is with a clinometer. This is a small handheld device with a sighting lens and crosshair and one of a variety of different mechanisms for measuring the inclination angle (either positive or negative) of the sight-line from horizontal. Figure 10.7 illustrates the hypothetical triangles constructed with vertices at the observer’s eye, and the base and crown of the target tree. Obtaining the height distribution of merchantable timber in our forest parcel in Problem 4.5 could include a set of representative height measurements with a clinometer.
In measuring the height of a tree, two readings are often taken with the clinometer: one to the crown [latex]\theta_{u}[/latex] and one to the base or stump [latex]\theta_{l}[/latex]. The observation point E is a pre-determined distance D from the tree itself. From this information, what is the height of the tree?
We identify H as the quantity of interest, and observe that [latex]H = H_u + H_l[/latex]. As a first step, we must therefore determine [latex]H_u[/latex] and [latex]H_l[/latex]. We assume the geometry of the problem allows us to construct two imaginary right triangles as illustrated and that our clinometer gives us angles in degrees from the horizontal. Since we know the horizontal distance to the tree D and have measured the angles to the top ([latex]\theta_u[/latex]) and bottom ([latex]\theta_l[/latex]) of the tree, we know the adjacent side length (D) and an angle for both triangles. The target unknowns are the opposite sides of each triangle, and from sohcahtoa we know that we can use [latex]\tan[/latex] to find the opposite sides when we know the adjacent sides. Thus:
[latex]\tan{\theta_u}=\frac{H_u}{D} \tag{10.10}[/latex]
[latex]D\tan{\theta_u}=H_u \tag{10.11}[/latex]
and
[latex]\tan{\theta_l}=\frac{H_l}{D} \tag{10.12}[/latex]
[latex]D\tan{\theta_l}=H_l \tag{10.13}[/latex]
and since [latex]H = H_u + H_l,[/latex]
[latex]H = D\tan{\theta_u} + D\tan{\theta_l} \tag{10.14}[/latex]
[latex]H = D(\tan{\theta_u} + \tan{\theta_l}). \tag{10.15}[/latex]
Thus, we can use an elementary trigonometric function (tan) and a bit of algebra to produce a formula that relates clinometer angle measurements to tree height.
10.4 Arbitrary triangles

While some problems may be approached profitably with imaginary right triangles, others present triangles without right angles. We’ll call these arbitrary or general triangles. Triangulation is a typical task in which ecologists or wildlife managers might encounter arbitrary triangles. When radio-tracking a collared animal, for example, one method for determining the animal’s location at a given time is by triangulation from multiple directional antennae. Figure 10.8 is the same as Figure 10.1, except that now we are considering the vertices to be radio transmitters (animals) and receivers (ecologists).
Thus far, we only have two tools that are safe to use with triangles that lack a right angle: the rule that all the interior angles sum to 180° (for which we may use the shorthand ([latex]\Sigma\angle180[/latex]) and the general criteria for and implications of similar triangles. These might be of limited use if our goal is to determine the distance to or location of a collared animal. But if we know the length of one side (say side b in Figure 10.8), and a few angles, we can make some progress.
10.4.1 Law of sines
The law of sines is valid for general triangles, including right triangles. If we are careful to define our sides and vertices as we have (with vertex angle A opposite side a and so on), we can state the law of sines as follows:
Law of Sines
[latex]\large{\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}.} \tag{10.16}[/latex]
Note that this equation is strange in that there are two equals signs. Don’t get worried, this is just a shorthand that allows us to say on one line that each ratio between the sine of an angle and the length of its opposite side is equal to the other corresponding sine/side ratios. If we wrote each equation with a single ‘=’, there would be three of them and it would simply take more space. But in actual implementation you can use any of the implied equalities in Equation 10.16, such as:
[latex]\large{\frac{\sin{A}}{a}=\frac{\sin{C}}{c}.}\tag{10.17}[/latex]
The key concept here is that there is a simple and consistent relationship between the sine of each angle and the length of its opposite side, and that this applies to all triangles, no matter what size or shape. That makes plenty of sense right? If you imagine taking a triangle formed by three knotted rubber bands and lengthening one side (without changing the length of the other sides), what happens to the angle opposite that stretched side? It grows right? But to accommodate the growth of that angle, the other two angles must get smaller. The law of sines is especially helpful if you know two sides and one angle (SSA) or two angles and one side (AAS).
10.4.2 Law of cosines
Another tool that is useful for general triangles is called the “Law of cosines”. In many ways, it provides the same information that you can easily find from other tools we have already discussed, so we won’t derive it or discuss it in great detail. But mathematician Paul Lockhart makes the case that the law of cosines might be a misleading name, and that the relationship might be better described as a modified version of the Pythagorean theorem that is good for all general triangles. Check it out:
[latex]c^2 = a^2 + b^2 - 2ab\cos{C}. \tag{10.18}[/latex]
As you can see, it is identical to the Pythagorean theorem except that there is a correction factor [latex]2ab\cos{C}[/latex] that is subtracted to account for deviations from a right triangle. As with the Pythagorean theorem, the law of cosines gives you the third side length if you know the other two, but you also need to know the angle between the known sides (SSA). As such, it’s function overlaps that of the law of sines.
10.5 Triangle tools: A summary
Trigonometry is a large subdiscipline of mathematics, and can and does fill more than a semester in math classes. Our treatment here has focused on the tools that are most commonly encountered in practical field settings in the natural sciences. Many additional functions, relationships and skills can become important in specific, more technical applications, but most of these can be derived from the basic functions discussed here. These functions and properties are summarized in the table that follows.
| Rule name | Relationship | right | general | use for |
|---|---|---|---|---|
| Angle sum | [latex]\sum{\angle}=180^{\circ}[/latex] | X | X | AA known, want A |
| Pythagorean theorem | [latex]c^2 = a^2 + b^2[/latex] | X | SS known, want S | |
| Similarity | [latex]X_1 = CX_2[/latex] | X | X | C known, want X (A,S or other) |
| sine | [latex]\sin{\theta} = O/H[/latex] | X | AS(O or H) known, want S(H or O) | |
| cosine | [latex]\cos{\theta} = A/H[/latex] | X | AS(A or H) known, want S(H or A) | |
| tangent | [latex]\tan{\theta} = O/A[/latex] | X | AS(O or A) known, want S(A or O) | |
| Law of sines | [latex]\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}[/latex] | X | X | AAS or SSA known, want S |
| Law of cosines | [latex]c^2 = a^2 + b^2 - 2ab\cos{C}[/latex] | X | X | SSA known, want S |
Example: shoreline waterfowl habitat (Problem 4.1)
Some dabbling duck species like Mallards seem to prefer very shallow water. This means that small, shallow wetlands can fit the bill, but even the shallow shoreline areas of larger and deeper wetlands may be adequate. Shorelines are also the interface between feeding and nesting areas for many species, and often support diverse flora and fauna across the ecotone.
One way we could estimate the extent of shoreline habitat is to find the length of wetland perimeters, or outlines. If, as described in the last chapter, we have digitized (or obtained existing data for) the outlines of wetlands in our candidate parcels, we should have easting and northing coordinates for these outlines. As with polygon area, most GIS software will automatically compute the perimeter of any shape. However, it is instructive to see how this follows from our earlier discussion of triangle-assisted spatial reasoning.
Recall that when we were traversing between dickcissel nests, we used an implementation of the Pythagorean theorem to find the straight-line distance from the coordinates of both end points. We can write this relationship in an x, y coordinate system as follows:
[latex]l_{1\rightarrow2} = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]}, \tag{10.19}[/latex]
where [latex]l_{1\rightarrow2}[/latex] is the length of the straight-line distance from point 1 (with coordinates x1, y1) and point 2. Notice that the result is always a real, non-negative number because the differences are squared. If we have a series of n points describing the wetland outlines, the sum of all n of the lengths forming a closed polygon approximate the perimeter P of the polygon.[4] We can generalize this as follows:
[latex]\begin{gathered} P = \sqrt{[(x_2 - x_1)^2 + (y_2 - y_1)^2]} + \sqrt{[(x_3 - x_2)^2 + (y_3 - y_2)^2]} + ...\\ ... \sqrt{[(x_1 - x_n)^2 + (y_1 - y_n)^2]}.\end{gathered} \tag{10.20}[/latex]
As with the trapezoidal area formula, this can be implemented by hand, in a spreadsheet, or with GIS software.
Exercises
- Use Figure 10.8 and the right triangles formed by dropping the perpendicular h, to derive the law of sines from the trig functions you already know.
- Explain how you could find the telemetered location of B if you know the locations of A and C and their internal angles.
- What happens if you try to apply the law of sines to a right triangle?
- What happens if you use the law of cosines on a right triangle? Assume angle C is the right angle.
- Triangles can be used to measure distant objects, even if we can’t get to them. This can be used to estimate the height of an object (e.g., a mountain peak or tree) where we cannot access the base, and therefore cannot measure the full horizontal distance that separates us from the object we wish to measure.
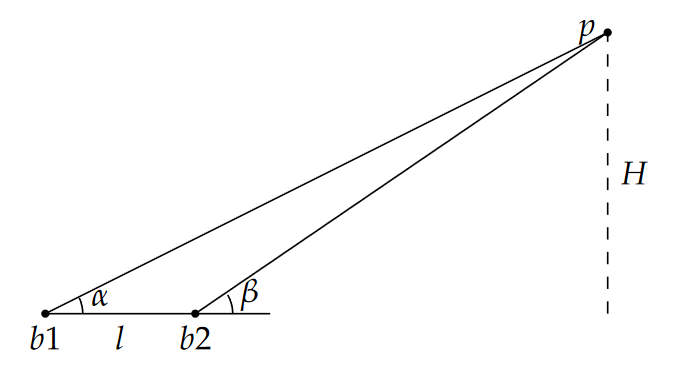
Figure 10.9: Triangle abstraction of the mountain problem. The general premise of the remote method is illustrated in Figure 10.9. If we can use a clinometer (a device for determining the angle between horizontal and a sight-line to an object of interest) to determine the sight-line angles to the object of interest p from two different places b1 and b2, and we know the distance between those places l, we can use trigonometry and algebra to determine the desired height H.
Devise a strategy for measuring H from the information gathered at b1 and b2. Derive and justify a formula that can be used for this task.
- At this point you may just need to take my word for it, but I hope that you’ll appreciate this fact by the time you finish this chapter. ↵
- In some fields this concept is endowed with a more sophisticated sounding name: geometric similitude. ↵
- In math and physics, angles are also frequently measured in radians rather than degrees. Note also that many computer programs that are able to do trigonometric computations assume that your argument (or desired result) will be in radians. Radians make alot of sense for geometry because, by definition a radian is the angle traversed when you traverse a length along the perimeter of the circle that is equal to the radius of the circle. But for practical use in the field, degrees are easier to work with. So here’s a quick rule of thumb in case you need to convert: once around a circle is 360° and 2π radians. ↵
- How good is this sort of approximation of the perimeter? This is a simple question with a not-so-simple answer. For our purposes here, the more points we have, the better – particularly if we’ve got an automated way to do the computations. However, in a more philosophical sense this is the crux of the coastline paradox, first popularized by mathematician Benoit Mandelbrot. ↵
In our context, the word isometric means that any change in one spatial dimension of a shape (e.g., length) is matched by a proportional change in all other dimensions.
A right triangle is defined as a triangle with one right, or 90° angle.

