5 Distillation
Introduction to Distillation
![]() = mass or molar flow rate of the bottoms stream leaving the systems (mass time-1 or mole time-1)
= mass or molar flow rate of the bottoms stream leaving the systems (mass time-1 or mole time-1)
![]() = mass or molar flow rate of the distillate stream leaving the system (mass time-1 or mole time-1)
= mass or molar flow rate of the distillate stream leaving the system (mass time-1 or mole time-1)
![]() = mass or molar flow rate of the feed stream entering the system (mass time-1 or mole time-1)
= mass or molar flow rate of the feed stream entering the system (mass time-1 or mole time-1)
![]() = mass or molar flow rate of the liquid reflux returned to the column from the condenser (mass time-1 or mole time-1); also generic flow rate of the liquid phase in the rectifying section
= mass or molar flow rate of the liquid reflux returned to the column from the condenser (mass time-1 or mole time-1); also generic flow rate of the liquid phase in the rectifying section
![]() = mass or molar flow rate of the liquid leaving the bottom of the column and entering the reboiler (mass time-1 or mole time-1); also generic flow rate of the liquid phase in the stripping section
= mass or molar flow rate of the liquid leaving the bottom of the column and entering the reboiler (mass time-1 or mole time-1); also generic flow rate of the liquid phase in the stripping section
![]() = generic stage number, stage 1 is at the top of the column
= generic stage number, stage 1 is at the top of the column
![]() = reflux ratio
= reflux ratio
![]() = mass or molar flow rate of vapor leaving the top of the column and entering the condenser (mass time-1 or mole time-1); also generic flow rate of the vapor phase in the rectifying section
= mass or molar flow rate of vapor leaving the top of the column and entering the condenser (mass time-1 or mole time-1); also generic flow rate of the vapor phase in the rectifying section
![]() = mass or molar flow rate of the gaseous boilup returned to the column from the reboiler (mass time-1 or mole time-1); also generic flow rate of the vapor phase in the stripping section
= mass or molar flow rate of the gaseous boilup returned to the column from the reboiler (mass time-1 or mole time-1); also generic flow rate of the vapor phase in the stripping section
![]() = mass or mole fraction of the light key in a liquid stream
= mass or mole fraction of the light key in a liquid stream
![]() = mass or mole fraction of the light key in the bottoms stream
= mass or mole fraction of the light key in the bottoms stream
![]() = mass or mole fraction of the light key in the distillate stream
= mass or mole fraction of the light key in the distillate stream
![]() = mass or mole fraction of the light key in the liquid leaving stage
= mass or mole fraction of the light key in the liquid leaving stage ![]()
![]() = mass or mole fraction of the light key in vapor stream
= mass or mole fraction of the light key in vapor stream
![]() = mass or mole fraction of the light key in the vapor leaving stage
= mass or mole fraction of the light key in the vapor leaving stage ![]()
![]() = mass or mole fraction of the light key in the feed stream
= mass or mole fraction of the light key in the feed stream
Overall material balance
(20.1) ![]()
Material balance on light key
(20.2) ![]()
Combination of material balances in Equations 20.1 and 20.2
(20.3) ![]()
(20.4) ![]()
(20.5) ![]()
Material balance on stages ![]() , the rectifying section of the column
, the rectifying section of the column
(20.6) ![]()
Rectifying section operating line
(20.7) ![]()
Stripping section operating line
(20.8) ![]()
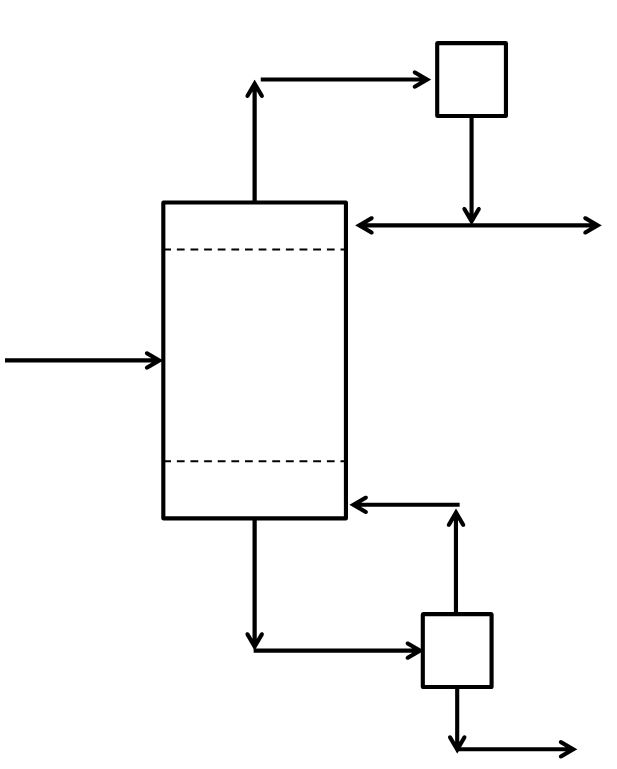
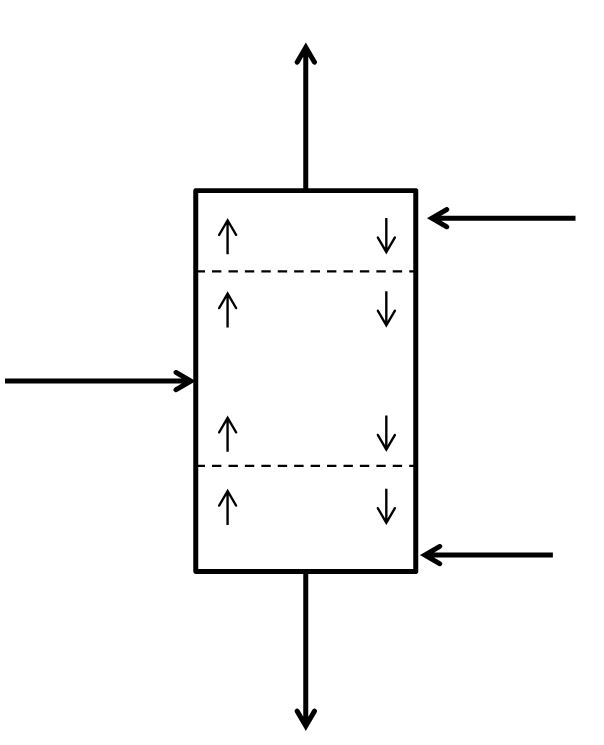

McCabe-Thiele Method for Finding N and Feed Stage Location
![]() = enthalpy change of vaporization of the feed stream at the column operating pressure (energy mole-1)
= enthalpy change of vaporization of the feed stream at the column operating pressure (energy mole-1)
![]() = heat capacity of the liquid feed stream (energy mole-1 temperature-1)
= heat capacity of the liquid feed stream (energy mole-1 temperature-1)
![]() = heat capacity of the vapor feed stream (energy mole-1 temperature-1)
= heat capacity of the vapor feed stream (energy mole-1 temperature-1)
![]() = molar flow rate of the feed stream entering the system (mole time-1)
= molar flow rate of the feed stream entering the system (mole time-1)
![]() = molar flow rate of the liquid phase in the rectifying section (mole time-1)
= molar flow rate of the liquid phase in the rectifying section (mole time-1)
![]() = molar flow rate of the liquid phase in the stripping section (mole time-1)
= molar flow rate of the liquid phase in the stripping section (mole time-1)
![]() = molar flow rate of the liquid portion of the feed stream (mole time-1)
= molar flow rate of the liquid portion of the feed stream (mole time-1)
![]() = generic stage number, stage 1 is at the top of the column
= generic stage number, stage 1 is at the top of the column
![]() = metric that reflects the physical state of the feed stream (unitless)
= metric that reflects the physical state of the feed stream (unitless)
![]() = reflux ratio
= reflux ratio
![]() = bubble-point temperature of the feed stream at the column operating pressure (temperature)
= bubble-point temperature of the feed stream at the column operating pressure (temperature)
![]() = dew-point temperature of the feed stream at the column operating pressure (temperature)
= dew-point temperature of the feed stream at the column operating pressure (temperature)
![]() = temperature of the feed stream (temperature)
= temperature of the feed stream (temperature)
![]() = molar flow rate of the vapor phase in the rectifying section (mole time-1)
= molar flow rate of the vapor phase in the rectifying section (mole time-1)
![]() = molar flow rate of the vapor phase in the stripping section (mole time-1)
= molar flow rate of the vapor phase in the stripping section (mole time-1)
![]() = molar flow rate of the vapor portion of the feed stream (mole time-1)
= molar flow rate of the vapor portion of the feed stream (mole time-1)
![]() = mole fraction of the light key in the bottoms stream
= mole fraction of the light key in the bottoms stream
![]() = mole fraction of the light key in the distillate stream
= mole fraction of the light key in the distillate stream
![]() = mole fraction of the light key in the liquid leaving stage
= mole fraction of the light key in the liquid leaving stage
![]() = mole fraction of the light key in the feed stream
= mole fraction of the light key in the feed stream
Finding the Theoretical Number of Stages from known Reflux Ratio, Boilup Ratio, Distillate Composition and Bottoms Composition
Rectifying section operating line
(21.1) ![]()
Stripping section operating line
(21.2) ![]()
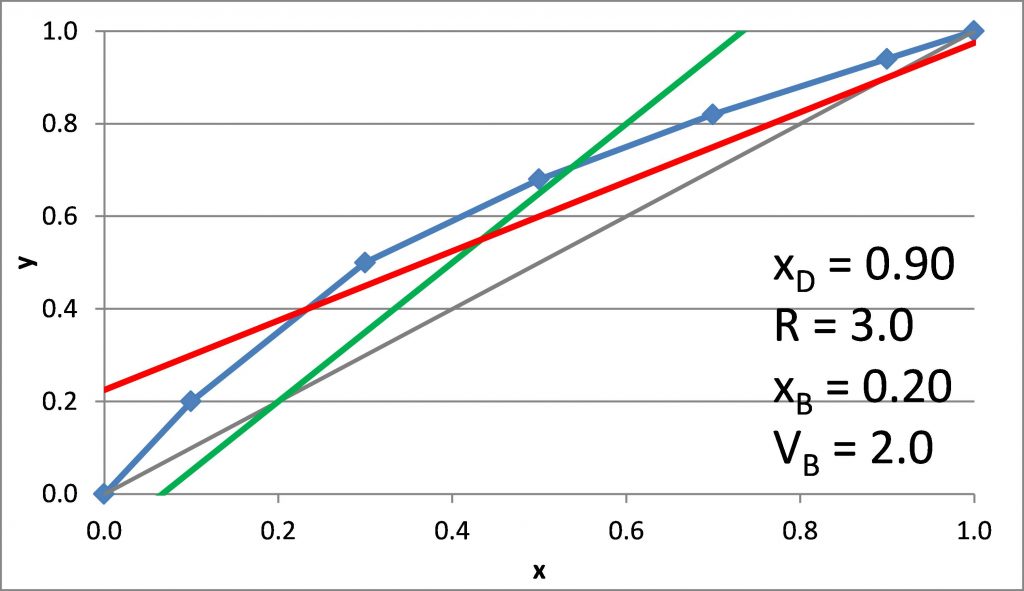
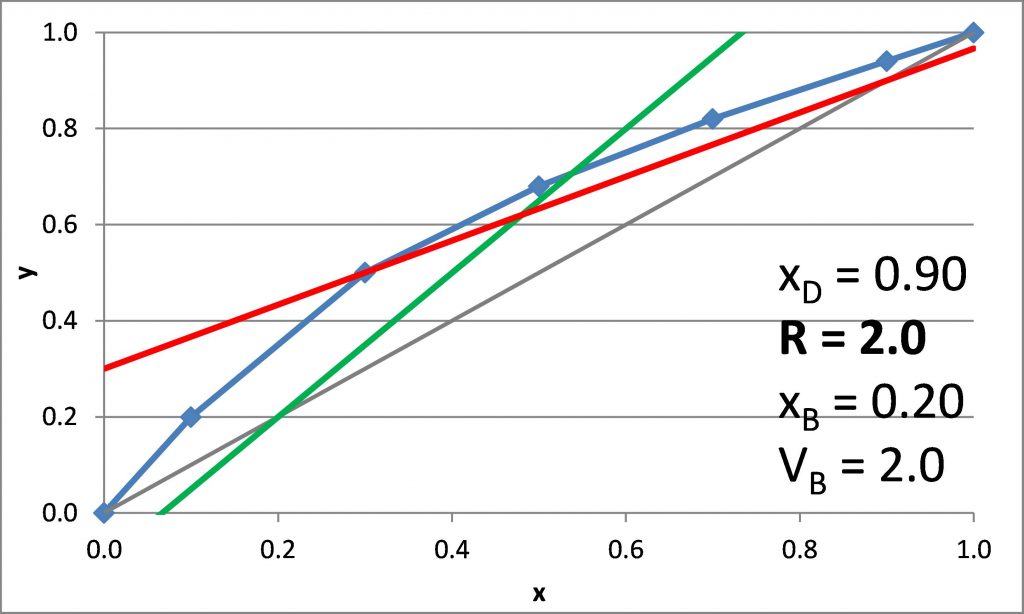
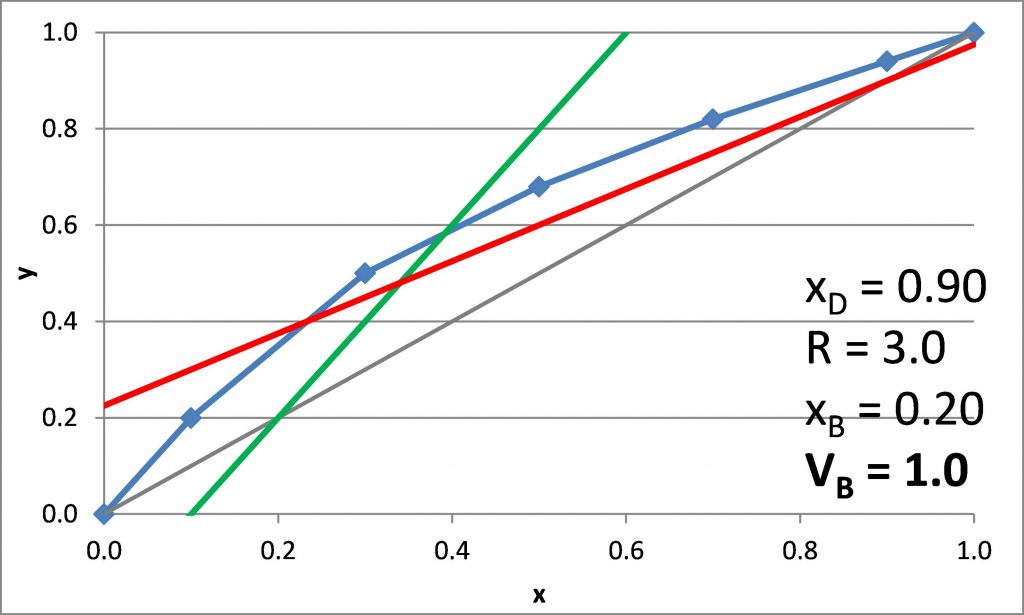
Plotting the q-line
(21.3) ![]()
(21.4) ![]()
For sub-cooled liquid, q > 1
(21.5) ![]()
For a saturated liquid,
(21.6) ![]()
For a mixture of liquid and vapor, 0 < q < 1
(21.7) ![]()
For a saturated vapor, q = 0
(21.8) ![]()
For sub-heated vapor, q < 0
(21.9) ![]()
q-line
(21.10) ![]()
Watch this two-part video series from LearnChemE that demonstrates how to use the McCabe-Thiele graphical method to determine the number of equilibrium stages needed to meet a specified separation objective: McCabe-Thiele Graphical Method Example Part 1 (8:21) and McCabe-Thiele Graphical Method Example Part 2 (6:35).
Watch this video from LearnChemE for a conceptual demonstration of how to relate stepping off stages to distillation column design: McCabe-Thiele Stepping Off Stages (7:02):
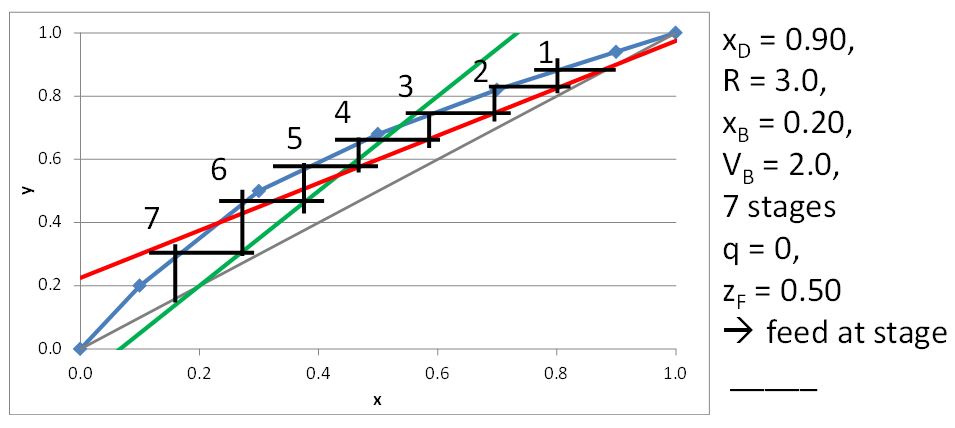
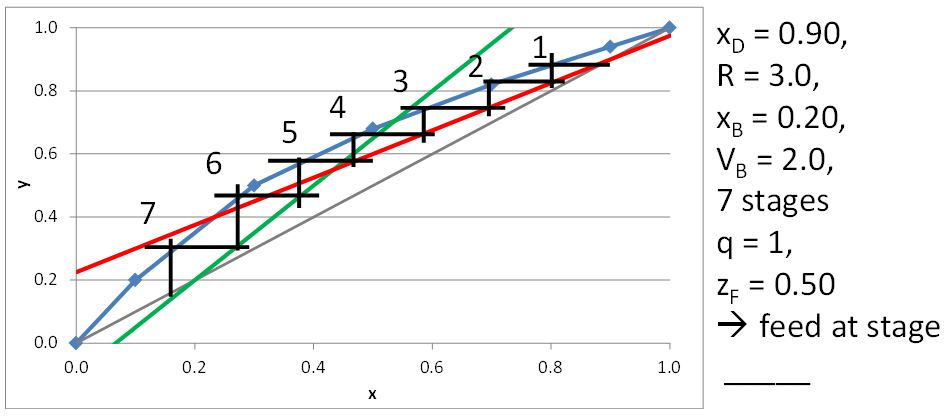
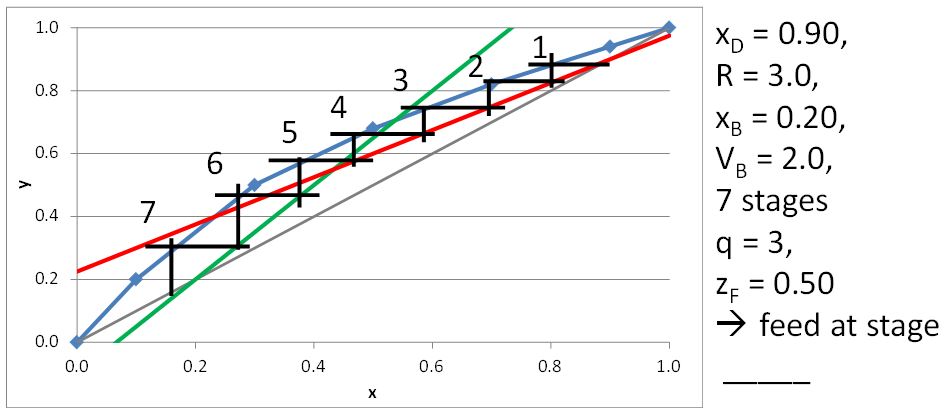
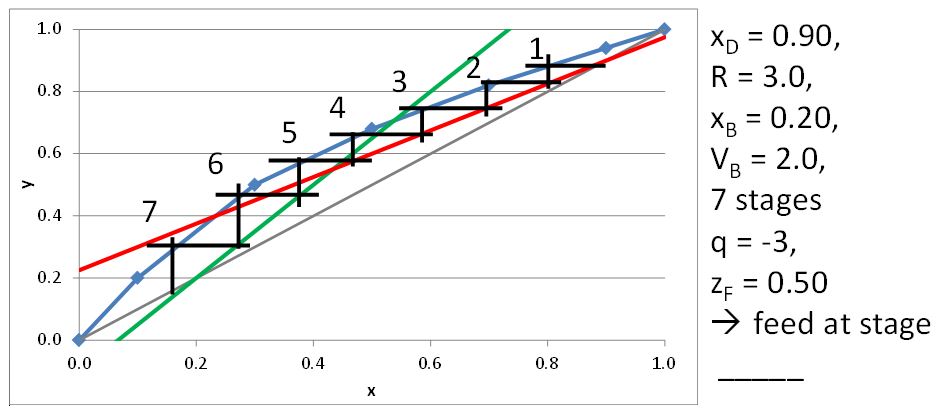
McCabe-Thiele Method for Finding the Minimum Number of Stages, the Minimum Reflux Ratio, and the Minimum Boilup Ratio
![]() = relative volatility of the light key and the heavy key at a given temperature (unitless)
= relative volatility of the light key and the heavy key at a given temperature (unitless)
![]() = relative volatility of the light key and the heavy key at the feed temperature (unitless)
= relative volatility of the light key and the heavy key at the feed temperature (unitless)
![]() = activity coefficient of the heavy key; can be a function of
= activity coefficient of the heavy key; can be a function of ![]() and/or
and/or ![]() ; 1 for an ideal solution (unitless)
; 1 for an ideal solution (unitless)
![]() = activity coefficient of the light key; can be a function of
= activity coefficient of the light key; can be a function of ![]() and/or
and/or ![]() ; 1 for an ideal solution (unitless)
; 1 for an ideal solution (unitless)
![]() = molar flow rate of the bottoms leaving the system (mol time-1)
= molar flow rate of the bottoms leaving the system (mol time-1)
![]() = molar flow rate of the distillate leaving the system (mol time-1)
= molar flow rate of the distillate leaving the system (mol time-1)
![]() = molar flow rate of the feed stream (mol time-1)
= molar flow rate of the feed stream (mol time-1)
![]() = molar flow rate of liquid within the rectifying section, assumed constant in McCabe-Thiele model (mol time-1)
= molar flow rate of liquid within the rectifying section, assumed constant in McCabe-Thiele model (mol time-1)
![]() = molar flow rate of liquid within the stripping section, assumed constant in McCabe-Thiele model (mol time-1)
= molar flow rate of liquid within the stripping section, assumed constant in McCabe-Thiele model (mol time-1)
![]() = minimum required number of theoretical stages for a given combination of equilibrium data,
= minimum required number of theoretical stages for a given combination of equilibrium data, ![]() and
and ![]()
![]() = saturated vapor pressure of the heavy key at a given temperature, i.e. by Antoine equation (pressure)
= saturated vapor pressure of the heavy key at a given temperature, i.e. by Antoine equation (pressure)
![]() = saturated vapor pressure of the light key at a given temperature, i.e. by Antoine equation (pressure)
= saturated vapor pressure of the light key at a given temperature, i.e. by Antoine equation (pressure)
![]() = metric that indicates that physical state of the feed stream, i.e.
= metric that indicates that physical state of the feed stream, i.e. ![]() = 1 for saturated liquid (unitless)
= 1 for saturated liquid (unitless)
![]() = reflux ratio =
= reflux ratio = ![]() (unitless)
(unitless)
![]() = reflux ratio that requires an infinite number of stages in the rectifying section (unitless)
= reflux ratio that requires an infinite number of stages in the rectifying section (unitless)
![]() = molar flow rate of vapor within the rectifying section, assumed constant in McCabe-Thiele model (mol time-1)
= molar flow rate of vapor within the rectifying section, assumed constant in McCabe-Thiele model (mol time-1)
![]() = molar flow rate of vapor within the stripping section, assumed constant in McCabe-Thiele model (mol time-1)
= molar flow rate of vapor within the stripping section, assumed constant in McCabe-Thiele model (mol time-1)
![]() = boilup ratio =
= boilup ratio = ![]()
![]() = boilup ratio that requires an infinite number of stages in the stripping section (unitless)
= boilup ratio that requires an infinite number of stages in the stripping section (unitless)
![]() = molar flow rate of the vapor component of the feed stream (mol time-1)
= molar flow rate of the vapor component of the feed stream (mol time-1)
![]() = target mole fraction of the light key in the bottoms product
= target mole fraction of the light key in the bottoms product
![]() = target mole fraction of the light key in the distillate product
= target mole fraction of the light key in the distillate product
![]() = mole fraction of the heavy key in the liquid phase
= mole fraction of the heavy key in the liquid phase
![]() = mole fraction of the light key in the liquid phase
= mole fraction of the light key in the liquid phase
![]() = mole fraction of the heavy key in the vapor phase
= mole fraction of the heavy key in the vapor phase
![]() = mole fraction of the light key in the vapor phase
= mole fraction of the light key in the vapor phase
![]() = mole fraction of the light key in the feed stream
= mole fraction of the light key in the feed stream
(22.1) ![]()
![]() = slope of the line that connects (
= slope of the line that connects (![]() ,
, ![]() ) to the intersection of the q-line and the equilibrium curve
) to the intersection of the q-line and the equilibrium curve
(22.2) ![]()
(22.3) ![]()
![]() = slope of the line that connects (
= slope of the line that connects (![]() ,
, ![]() ) to the intersection of the q-line and the equilibrium curve
) to the intersection of the q-line and the equilibrium curve
(22.4) ![]()
when ![]() ,
, ![]() ; when
; when ![]() ,
, ![]() ; when
; when ![]() ,
, ![]()
*we will use Eq 22.4 to calculate ![]() as a function of our selected
as a function of our selected ![]()
Example
![]() ,
, ![]() ,
, ![]()
![]() =
=
![]() =
=

Example
![]() ,
, ![]()
![]()
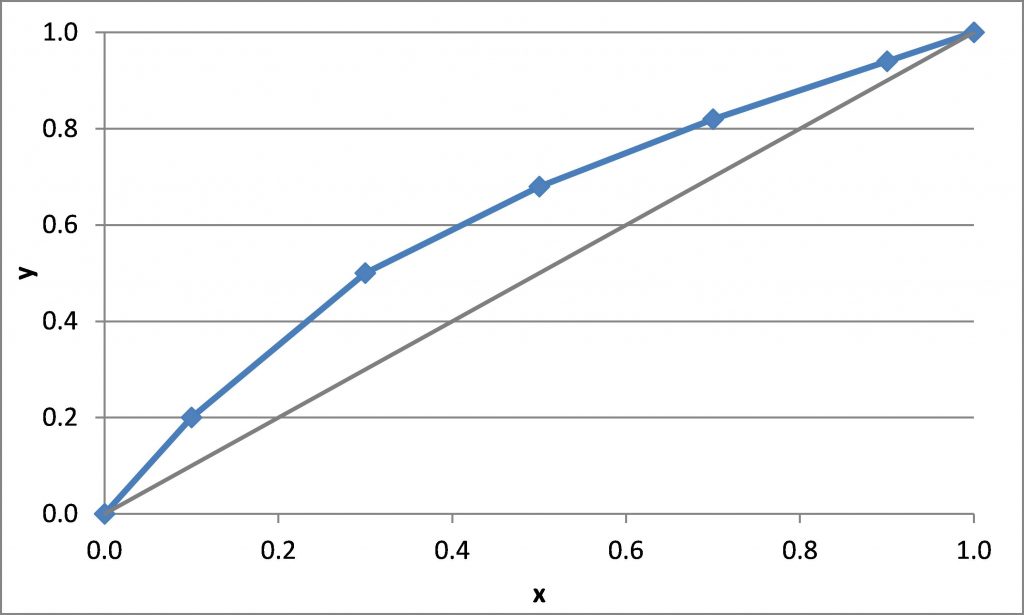
Distillation Energy Demand and Correlations for Efficiency
![]() = relative volatility of the light key and heavy key (unitless). For equation 23.2, this is evaluated at the average column temperature.
= relative volatility of the light key and heavy key (unitless). For equation 23.2, this is evaluated at the average column temperature.
![]() = average heat of vaporization for the stream entering the condenser or reboiler (energy mole-1)
= average heat of vaporization for the stream entering the condenser or reboiler (energy mole-1)
![]() = average heat of vaporization for the steam entering the reboiler (energy mole-1)
= average heat of vaporization for the steam entering the reboiler (energy mole-1)
![]() = liquid phase viscosity (cP). For eqs 23.1 and 23.2, this is the viscosity of the feed stream at the average column temperature.
= liquid phase viscosity (cP). For eqs 23.1 and 23.2, this is the viscosity of the feed stream at the average column temperature.
![]() = bottoms flow rate (mole time-1)
= bottoms flow rate (mole time-1)
![]() = heat capacity of liquid water (energy mole-1 temperature-1) or (energy mass-1 temperature-1)
= heat capacity of liquid water (energy mole-1 temperature-1) or (energy mass-1 temperature-1)
![]() = distillate flow rate (mole time-1)
= distillate flow rate (mole time-1)
![]() = stage efficiency (unitless)
= stage efficiency (unitless)
![]() = liquid flow rate in the rectifying section (mole time-1)
= liquid flow rate in the rectifying section (mole time-1)
![]() = liquid flow rate in the stripping section (mole time-1)
= liquid flow rate in the stripping section (mole time-1)
![]() = flow rate of cooling water to condenser (mass time-1) or (mole time-1)
= flow rate of cooling water to condenser (mass time-1) or (mole time-1)
![]() = flow rate of steam to reboiler (mass time-1) or (mole time-1)
= flow rate of steam to reboiler (mass time-1) or (mole time-1)
![]() = energy demand (cooling) for the condenser (energy time-1)
= energy demand (cooling) for the condenser (energy time-1)
![]() = energy demand (heating) for the reboiler (energy time-1)
= energy demand (heating) for the reboiler (energy time-1)
![]() = reflux ratio =
= reflux ratio = ![]() (unitless)
(unitless)
![]() = temperature of cooling water entering the condenser (temperature)
= temperature of cooling water entering the condenser (temperature)
![]() = temperature of cooling water leaving the condenser (temperature)
= temperature of cooling water leaving the condenser (temperature)
![]() = boilup ratio =
= boilup ratio = ![]() (unitless)
(unitless)
![]() = molar flow rate of the vapor portion of the feed (mole time-1)
= molar flow rate of the vapor portion of the feed (mole time-1)
Correlations for Stage Efficiency
Drickamer and Bradford
(23.1) ![]()
Restrictions on eq 23.1: ![]() cP,
cP, ![]() °F,
°F, ![]() psia,
psia, ![]() %
%
O’Connell
(23.2) ![]()
when ![]() , adjust
, adjust ![]() calculated by 23.2 with correction factor from Table 7.5
calculated by 23.2 with correction factor from Table 7.5
Restriction on eq 23.2: ![]()
Condenser and Reboiler Energy Demand
total condenser
(23.3) ![]()
partial reboiler
(23.4) ![]()
for partially vaporized feed ![]() and total condenser
and total condenser
(23.5) ![]()
(23.6) ![]()
if using saturated steam for the reboiler
(23.7) ![]()
Distillation Packed Column Depth
![]() = height of equivalent theoretical plates
= height of equivalent theoretical plates
![]() (length)
(length)
![]() = local slope of equilibrium curve/local slope of operating line
= local slope of equilibrium curve/local slope of operating line
(24.1) ![]()
Example
We aim to distill benzene and toluene to a distillate that contains 95 mol% benzene and a bottoms stream that contains 95% toluene. The feed stream is 100 kmol/hr of an equimolar mixture with q = 0.50. We will be operating at 1.0 atm, ![]() of 1.8 with a packed column containing 25-mm metal Bialecki rings. Assume operating at 70% of the flooding velocity. What depth of packing is needed to achieve this separation?
of 1.8 with a packed column containing 25-mm metal Bialecki rings. Assume operating at 70% of the flooding velocity. What depth of packing is needed to achieve this separation?
- For Antoine equation of the form
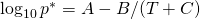 , where
, where 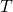 is in °C and
is in °C and 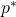 is in mmHg
is in mmHg
- Benzene:
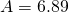 ,
, 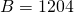 ,
, 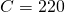
- Toluene:
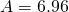 ,
, 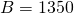 ,
, 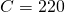
- Benzene:
- 25-mm metal Bialecki rings:
 ,
, 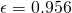 ,
, 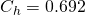 ,
, 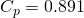 ,
, 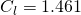 ,
, 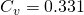 ,
, 
- Toluene:
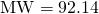 ,
, 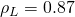 g/mL,
g/mL, 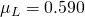 cP,
cP, 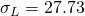 dyne/cm
dyne/cm - Benzene:
 ,
, 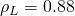 g/mL,
g/mL, 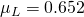 cP,
cP, 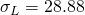 dyne/cm
dyne/cm 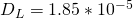 cm2/s (Table 3.4, Seader)
cm2/s (Table 3.4, Seader)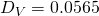 cm2/s (estimated via eq 3-36, Seader)
cm2/s (estimated via eq 3-36, Seader) cP, estimated from online gas viscosity calculator (LMNO Engineering) as a function of T (94°C)
cP, estimated from online gas viscosity calculator (LMNO Engineering) as a function of T (94°C)