3 EB-focused Strategies and Challenging Tasks
Ji-Yeong I and Ricardo Martinez
- What teaching strategies have you used (or heard of) for teaching mathematics to EBs? If you have used a strategy, how did it go?
- Which strategies do you think work best for teaching EBs mathematics? Do you think a strategy that worked for some EBs will work for others?
Here are some different scenarios from various classrooms. Read each scenario, and think about what strategy you would want to implement for each context.
You may notice we can make hundreds and thousands of different class scenarios like this. Even if you have EBs who speak the same first language or are from the same culture, the class they are in is an important factor in deciding how you will provide support for your EBs. We expect you came up with different strategies for each scenario, although some strategies may have been used more than once. If you have a specific math concept that you target for each class, you could probably find more specific strategies for teaching EBs. So, the math concept you teach also matters when developing an effective strategy for EBs.
Let’s recall an idea from the previous chapters.
In the Introduction, you read that EBs are not a homogeneous group. For this reason, your strategy will change depending on which EBs you have and in what class setting.
Here are more things you may need to consider when developing or choosing good strategies for EBs.
- What math concept will you teach?
- If the targeted math lesson is for conceptual understanding or procedural understanding…
- If the lesson involves abstract terms…
- If the lesson includes visuals like statistical graphs/charts, or geometric figures…
- Also, what skills or knowledge do you have?
- Can you speak the students’ native language?
- Are you familiar with teaching English either as a first language (Language/Communication Arts) or a second language?
- Are you confident in the specific math concept, so you can bring up many real-life examples?
Let’s recall another idea.
In the Introduction, you saw that not all supports are the same. Not all visuals are the same. Read this word problem and find a visual that provides more access to the math for EBs.
Problem: The distance from where I am to the magic school cafeteria is 6 km. My magic broom flies 2/3 km per minute. How many minutes will it take to get to the school cafeteria?
You will see two different visuals in the next slides. Think about which one would better support EBs. Ready? Click “next”
Visual 1:

Visual 2:
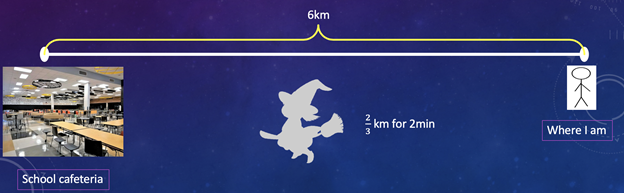
Which visual do you think will help give EBs better access to the math problem?
Why?
Let’s recall one more thing.
In the previous chapter, we learned about CSP, culturally sustaining pedagogy, and how important it is to have high expectations for all students and support them to sustain the culture and language they already have. You can see how a recommended strategy for EBs follows this pedagogical guidance in the second chapter of the book, Beyond Good Teaching (Celedon-Pattichis & Ramirez 2012). The authors provide guiding principles for teaching mathematics to EBs by considering the Common Core State Standards for Mathematics (National Governors Association Center for Best Practices & Council of Chief State School Officers, 2010) and the Process Standards of National Council of Teachers of Mathematics (NCTM, 2000).
- Challenging mathematical tasks
- Linguistically sensitive social environment
- Support for learning English while learning mathematics
- Mathematical tools and modeling as resources
- Cultural and linguistic differences as intellectual resources
The first principle, Challenging mathematical tasks, applies to all EBs at any level of English language development. The recommendation is clear: do not reduce the cognitive demand no matter what English level they are at, and no matter what mathematics level they are at. They deserve to receive an opportunity to learn rigorous mathematics with rich language activities. There should be high expectations for all students all the time.
- Do not reduce the cognitive demand,
- Do not remove a challenging aspect from a math problem, but
- Make the problem more accessible by…
- Including students’ familiar contexts and
- Providing appropriate support.
3 Act Task
As an example of challenging problems that integrate real-world contexts students are familiar with, we will introduce the 3 Act Task.
Dan Meyer, a thought leader in mathematics education, first developed and suggested using the 3 Act Task on his blog, dy/dan, and explained that students learn best in situations, “where students experience the world in concrete form, without the information that word problems typically provide, without sufficient resources to calculate.”
Just like the real-world problems we experience in our daily lives, a 3 Act Task does not include all the necessary information while textbook word problems do. Instead, the solvers of a 3 Act Task are supposed to identify what they need to solve the task and look for this information. This increases students’ cognitive demand, engagement, and ownership of knowledge. Let’s explore one example of the 3 Act Task.
This is the 3 Act Task. This strategy in itself may be already great for EBs and non-EBs, but if we further developed this concept into a 5 Act Task specifically for EBs we may be able to further support EBs language and mathematical development.
5 Act Task
For developing the 5 Act Task framework, we have added two new acts to the 3 Act Task: Act 0 and Act 4. Figure 3.1 shows the full cycle of the 5 Act Task framework. It is important to note that the five acts are not linear but iterative, meaning solvers can go back to any previous act as needed.
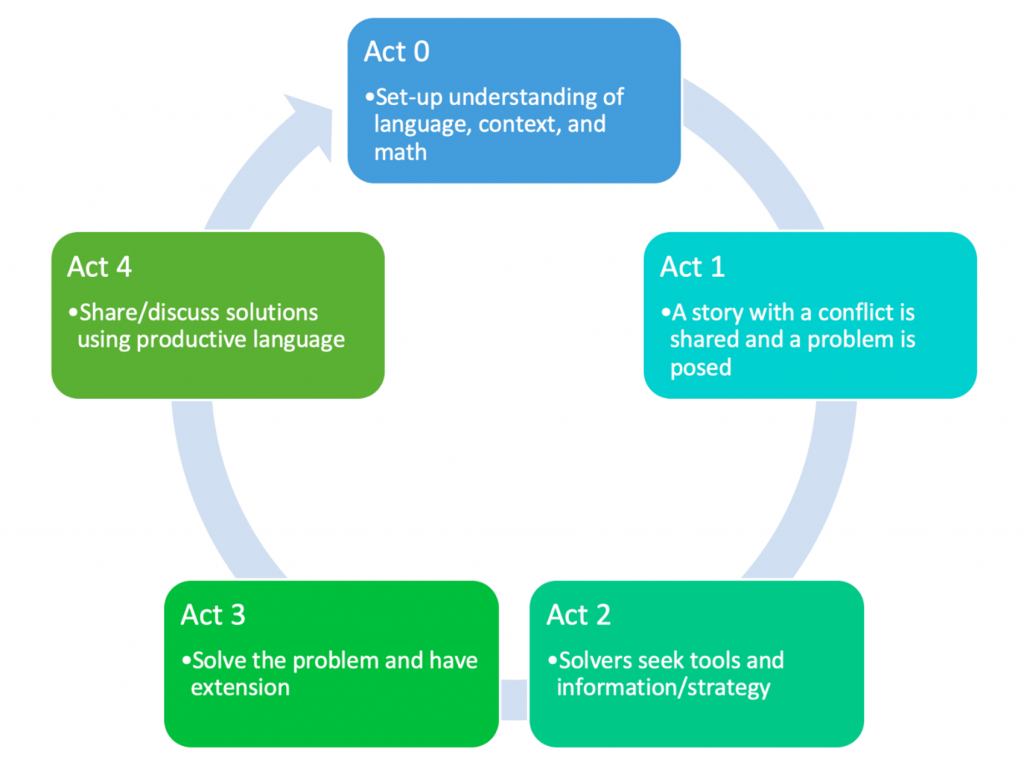
Act 0 is the most crucial step because it reflects a set-up stage where teachers support EBs’ understanding of both the language and the mathematics to be embedded in Act 1. For example, a teacher assesses EBs’ prior knowledge as it relates to the story (e.g., ask “Do you know how big a penny is?” or “What is a pyramid?”) and provides appropriate scaffolding (e.g., show a penny or have students build a small pyramid with pennies). Act 0 benefits all students because it helps them better comprehend the problem’s context, but it is essential for EBs because unknown vocabulary or cultural nuances may prevent them from finding mathematical entry points.
Act 4 starts after students find their solutions when EBs communicate about their solutions and reasoning behind their models. Because Act 4 involves productive language modes (writing and speaking), it can be challenging for EBs but simultaneously can provide a crucial opportunity for them to develop their English proficiency. To reduce EBs’ anxiety of speaking English and to maximize their learning, teachers should design Act 4 carefully by applying various strategies, such as: having group/pair presentations, allowing EBs to explain with visuals and gestures, giving enough time to prepare what to say in English, using a graphic organizer, and writing sentence frames on the board.
The following table shows the purpose of each act of the 5 Act Task Framework. Remember the five acts do not have to be linear or follow a sequence. Teachers can flexibly revisit any of the acts as necessary.
| Description | Purpose | |
| Act 0 | Assessing/scaffolding before Act 1
|
To support EBs by providing background knowledge of the problem’s language, context, and mathematics. |
| Act 1 | A story with conflict via multimedia/visuals/physical movements and problem-posing based on the story | To engage EBs in a relevant, real-life story towards an authentic understanding of the mathematical situation and to empower EBs by having them pose their own problem(s). |
| Act 2 | Student-driven collection of information to solve the problem they posed | To give EBs the agency to reflect on the story and develop their own assumptions to solve them. |
| Act 3 | Model construction with solution(s)
|
To provide EBs with an opportunity to visualize/model their mathematical process, to analyze and improve their decisions in the real world. |
| Act 4 | Collective communication of solutions/thinking process | To support EBs as they develop English proficiency while also building mathematical competency. |
Now, why don’t you google “3 Act Task?” You will see numerous resources and sample tasks on many websites. Some of them are already matched with Common Core State Standards for Mathematics, so it is convenient for teachers to implement them in their classes. Save them as your resources and properly revise them with our 5 Act Task for the EBs in your classrooms.
- How do you think you can figure out what context students are familiar with and what real-life situations might be engaging for them?
- What do you think would be the most challenging part for teachers of EBs when teaching a 5 Act Task lesson?
- You read that it is important to provide EBs with challenging math problems, however, your students may resist and complain that the problem is too difficult. How would you help them engage in solving challenging problems?
References
Celedon-Pattichis, S., & Ramirez, N. G. (Eds.). (2012). Beyond good teaching: Advancing mathematics education for ELLs. National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (2000). Principles and Standards for School Mathematics. National Council of Teachers of Mathematics.
National Governors Association Center for Best Practices, & Council of Chief State School Officers. (2010). Common core state standards for mathematics. National Governors Association Center for Best Practices, Council of Chief State School Officers. Washington, D.C.

