Chapter 8: Inheritance of Quantitative Traits
Laura Merrick; Kendra Meade; Arden Campbell; Deborah Muenchrath; Shui-Zhang Fei; William Beavis; and Walter Suza
Introduction
Many of the traits that plant breeders strive to improve are quantitatively inherited. For example, breeding efforts targeting quantitative traits have allowed major increases in crop yield during the past 80 years or so. A quantitatively inherited trait is controlled by many genes at different loci, with each gene — known as a polygene — contributing a small effect to the expression of the character. Polygenes are also known quantitative trait loci (QTL). QTLs involved in expression of a quantitative character act cumulatively to determine the phenotype of the trait. Their mode of inheritance is called quantitative genetics. Quantitative genetics describes the connection between phenotype and genotype and provides tools to show how phenotypic selection of complex characters changes allele frequencies.
Quantitative genetics focuses on the nature of genetic differences, seeks to determine the relative importance of genetic vs. environmental factors, and examines how phenotypic variation relates to evolutionary change. Typically, quantitative genetic analysis is executed on traits showing a continuous range of values. Analysis of quantitative traits is based on statistical predictions of population response. Examples of quantitatively inherited traits include yield, vigor, rate of photosynthesis, protein content, and drought tolerance.
Key Concepts
Central to the mathematical modeling of quantitative genetics is the concept of recognition of family resemblance. If genes influence variation in a trait (and sources of environmental variation are minimized or controlled), related individuals would be expected to resemble one another more than unrelated ones. Siblings should resemble each other more than distantly related relatives. A comparison of plant individuals with different degrees of relatedness provides information about how much genes influence the character.
Several factors influence the likelihood of progress when breeding for quantitatively inherited traits, including:
- Interaction of the multiple genes contributing to the phenotype;
- Gene actions of the respective genes involved; and
- Frequencies of those genes.
Various models are used to distinguish genetic, environmental, and genetic x environmental interaction effects on phenotype and to improve breeding efficiency of quantitative traits.
- Distinguish environmental and hereditary variation and be aware of why detecting the interaction of genetic and environmental factors is important.
- Understand the attributes of quantitative inheritance.
- Be familiar with statistical methods applied to quantitative inheritance.
- Study the types of gene actions and interactions affecting quantitative traits.
- Examine the genetic advance from selection formula and be able to explain how each of its components influences the improvement of the selected characteristic.
- Learn the types of heritability estimates and their importance in plant breeding.
Heritable vs. Environmental Variation
The phenotype of a plant or group of plants is modeled as a function of its genotype as modified by the environment.
Phenotype = Genotype + Environment + (Genotype x Environment)
[latex]P = G + E + (G \times E)[/latex]
Some characters are more responsive or sensitive to growing conditions than others. Qualitative traits such as flower color are not strongly influenced by the environment. On the other hand, quantitative traits such as grain yield or abiotic stress tolerance are influenced markedly by the environment. The degree of sensitivity or the range of potential responses to the environment is determined by the genetic composition of the individual plant or population of plants.
Genetic variation is essential in order to make progress in cultivar improvement. However, sources of variation include:
- Environmental variation
- Genetic variation and
- Interaction of genetic and environmental variation
Plant breeders must distinguish among these sources of variation for the character of interest in order to effectively select and transmit the desired character or assemblage of characters to subsequent generations.
GxE Interaction Example
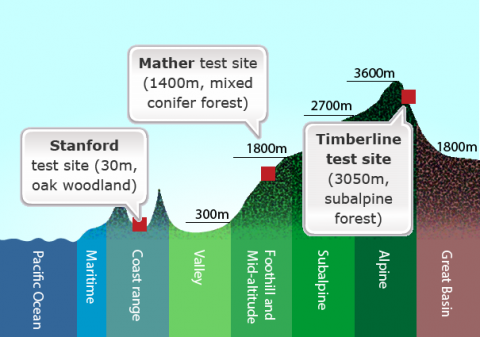
A classic example of genotype × environment interaction (GxE) involves studies conducted in the 1930s and 1940s by the ecologists Clausen, Keck, and Hiesey (1940, 1948). They collected plants from natural wild populations — principally yarrow (Achillea millefolia) and sticky cinquefoil (Potentilla glandulosa) — that grew along an east-west elevational transect in California, running from near sea level at the Pacific Ocean to more than 3000 m elevation in the Sierra Nevada mountains.
Both species exhibited a vast amount of variation in native populations with respect to growth form and other traits, including such attributes as plant height, winter survival, and number of stems produced. Through a series of reciprocal transplant experiments using cuttings or clonal material from wild populations, they tested the contribution of genetic and environmental variation to observed phenotypic variation among plants established in three main “common gardens” or transplant plots: Stanford, Mather, and Timberline (Fig. 1).
Conclusions
They concluded each species had differentiated into genetically distinct subspecies — which they called ecotypes — that are best suited to their specific environments. In the transplant gardens, no single ecotype performed best at all altitudes. For example, genotypes that produced the tallest plants at the mid-altitude garden site grew poorly at the low and high sites. Conversely, genotypes that grew the best at the low or high sites sometimes performed poorly at the mid-altitude site. Although within a species, all populations were found to be completely interfertile, ecotypes adapted to low or mid-altitude died when transplanted to the high altitude garden, while ecotypes from high elevations along the transect survived through the winter when locally grown in the test plots. GxE interaction was observed for height, among other characters.

Significance Illustration
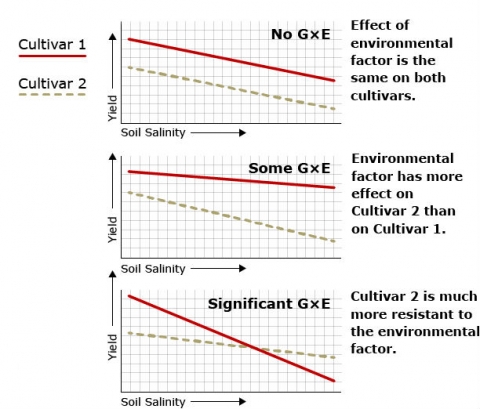
Figure 3 shows variation in phenotype between two cultivars of watermelon with regard to a quantitatively inherited trait (yield in this case) in response to variation in an environmental factor (soil salinity in this case) and illustrates the significance of genotype x environmental interaction.
Characteristics of Quantitative Traits

Inheritance of quantitative traits involves two or more nonallelic genes (multiple genes or polygenes); the combined action of these genes, as influenced by the environment, produces the phenotype. The effect of individual genes on the trait is not apparent. However, early in the 1900s it was discovered that the inheritance of the individual genes contributing to the phenotype of quantitative traits do indeed follow the same Mendelian inheritance principles as simply-inherited genes.
Inheritance of Quantitative Traits

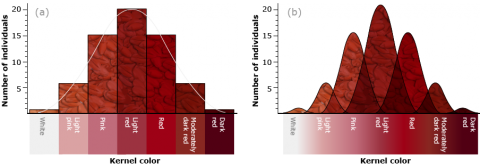
In 1909, Herman Nilsson-Ehle, a Swedish geneticist and wheat breeder, conducted some of the classic studies on quantitatively inherited traits in wheat. He developed what is known as the “Multiple Factor” or multi-factorial theory of genetic transmission. A key observation made by Nilsson-Ehle was that although a spectrum of continuous variation in kernel color (a quantitatively inherited trait influenced by environmental factors) could be observed in segregating generations, he was able to determine that segregation for these genes fit a model that each separate contributing gene followed a pattern of Mendelian inheritance.

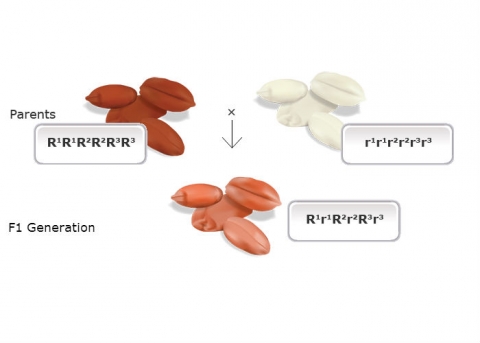
Bread wheat is a hexaploid — allopolyploid that contains three slightly different, but similar ancestral genomes (referred to as A, B, and D) in its genome (AABBDD). Depending on the cultivars that Nilsson-Ehle studied, each genome had a single gene that affected kernel color, and each of these loci has a red allele (R) and a white allele (r). Alleles at each locus varied slightly in their effect on kernel color, and will be designated in this example by different superscripts, e.g., R1 or r3.
He crossed two cultivars of wheat that varied in kernel color, one with dark red seeds (homozygous dominant genotype R1R1R2R2R3R3, based on the symbols designating the ancestral genomes) and another with white kernels (homozygous recessive r1r1r2r2r3r3). He noted that the F1 of a cross between these parents (heterozygote R1r1R2r2R3r3) was intermediate in color (light red), but the F2 generation could be grouped into seven classes, ranging in color from dark red to white. He explained the distribution on the basis of three pairs of genes segregating independently, with each dominant allele contributing to the intensity of the red color.
| F2 genotypes | Color | Number of dominant alleles | Number of plants out of 64 | ||
|---|---|---|---|---|---|
| R1R1R2R2R3R3 | dark red | 6 | 1 | ||
| R1R1R2R2R3r3 | R1r1R2R2R3R3 | R1R1R2r2R3R3 | moderately dark red | 5 | 6 |
| R1R1R2R2r3r3 r1r1R2R2R3R3 |
R1R1r2r2R3R3 R1r1R2r2R3R3 |
R1r1R2R2R3r3 R1R1R2r2R3r3 |
red | 4 | 15 |
| R1R1R2r2r3r3 R1R1r2r2R3r3 |
R1r1R2r2R3r3 R1r1R2R2r3r3 R1r1r2r2R3R3 |
r1r1R2R2R3r3 r1r1R2r2R3R3 |
light red | 3 | 20 |
| R1R1r2r2r3r3 r1r1R2R2r3r3 |
r1r1r2r2R3R3 R1r1R2r2r3r3 |
R1r1r2r2R3r3 r1r1R2r2R3r3 |
pink | 2 | 15 |
| R1r1r2r2r3r3 | r1r1R2r2r3r3 | r1r1r2r2R3r3 | light pink | 1 | 6 |
| r1r1r2r2r3r3 | white | 0 | 1 | ||
With three independent pairs of genes segregating, each with two alleles, as well as environmental effects acting on kernel color, the F2 progeny would contain 63 plants with varying shades of red kernels and one with white kernels. Linkage among the genes restricts independent assortment, so that the required size of the F2 population becomes larger.
Characteristics Indicative of Quantitative Inheritance
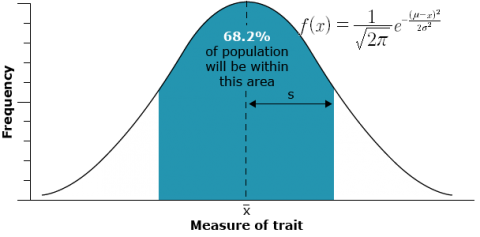
Phenotypic values for the specific trait, resulting from simultaneous segregation of multiple genes, exhibit continuous variation, rather than distinct classes. In general, the distribution of values of quantitatively inherited traits in a population follows a normal distribution (also called a Gaussian distribution or bell curve). These curves are generally characterized by two parameters, the mean and the variance or standard deviation. In the figure below, the mean of the random sample is depicted by the symbol  and the standard deviation by the symbol s. If the reference is made to a population instead of a sample from a population, the population mean is usually symbolized by μ and the population standard deviation by σ.
and the standard deviation by the symbol s. If the reference is made to a population instead of a sample from a population, the population mean is usually symbolized by μ and the population standard deviation by σ.
There are three general types of traits that are quantitatively inherited: continuous, meristic, and threshold. An example of the first type, a continuous trait, is fruit width of pineapple. The second type, a meristic character, is a countable trait that can take on integer values only, e.g., number of tillers of maize or branches of a rose bush. The third type of quantitative trait is known as a threshold character or “all-or-none” trait. Such traits are typically ranked simply as presence or absence, e.g., Downy Mildew disease in soybean.
Although they have only two phenotypes, threshold traits are considered to be quantitatively inherited because their expression depends on a liability (such as disease susceptibility or tolerance of nicotine levels) that varies continuously. Heritability of these traits is a function of the incidence of the trait in the population, so it is difficult to determine the importance of genetic factors in different environments or in different populations that differ in incidence. Threshold traits are assumed to be represented by an underlying normally distributed “liability trait” that is the sum of the independent genetic and environmental components of the distribution. A disease would have to be present before you could determine if certain genotypes were susceptible or not. For example, plants might be able to tolerate low to moderate levels of nicotine in their tissues until a threshold was crossed, above which the high level of nicotine present would be lethal.
Threshold characters exhibit only two phenotypes — the trait is either present or absent — but the susceptibility to the trait varies continuously and environmental components of the distribution. A disease would have to be present before you could determine if certain genotypes were susceptible or not. For example, plants might be able to tolerate low to moderate levels of nicotine in their tissues until a threshold was crossed, above which the high level of nicotine present would be lethal.
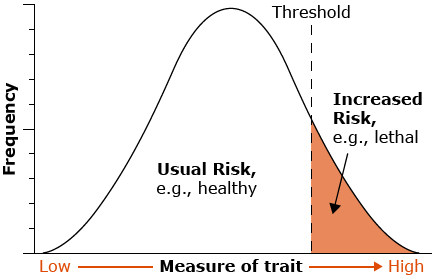
Threshold characters exhibit only two phenotypes — the trait is either present or absent — but the susceptibility to the trait varies continuously.
Environment has a large influence on the trait’s phenotype. That is, for the particular trait, the relative responses of plants change when grown under different environmental conditions.
Distinct segregation ratios of individual nonallelic genes are not observed. Recombination and segregation patterns are based on the combined effect of the polygenes on the trait. The more loci controlling the character, the greater the complexity.
Genes may differ in their individual gene action, but their effect on the trait is cumulative. Types of gene action include additive, dominance, overdominance and epistasis. Effects of gene action using the concepts of genotypic and breeding values are discussed in Appendix A.
The genotypic value is equal to
[latex]G = A + D + I[/latex]
- G = genotypic value of all loci considered together
- A = sum of all additive effects (i.e. breeding values) for separate loci
- D = sum of all dominance deviations (i.e., interaction between alleles at a locus or so-called intralocus interactions)
- I = interaction of alleles among loci (also referred to as the deviation or epistatic deviation)
For an individual, the breeding value is calculated by the summation of the average effects of its genes (also referred to as the additive effect of genes). The average effect of an allele is approximately the average deviation of the mean phenotypic value from the population mean if the allele at a particular locus is substituted by another allele (Falconer and Mackay 1996).
| No interaction among alleles |
Interaction among alleles |
|
|---|---|---|
| Within a locus | Additive | Dominance |
| Between loci | Additive | Epistasis |
Transgressive segregation may occur. These individuals exhibit phenotypes outside the range of those expressed by the parents. Transgressive segregation occurs when progeny contain new combinations of multiple genes with more positive effects or more negative effects for the quantitative trait than found in either parent. One challenge is that strong environmental effects would make it difficult to assess the mean performance in parental plants vs. progeny in order to detect for the presence of any transgressive segregants.
Measurement of Continuous Variation
Analysis of inheritance of qualitative traits is generally concerned with individual matings and their progeny and is made by counts and ratios. In contrast, analysis of quantitative traits is concerned with populations of organisms that consist of many possible kinds of matings; analysis of such traits is made by use of statistics. Statistical methods provide a tool for describing and evaluating quantitatively inherited characters. Since it is impractical to examine an entire population, plant breeders sample the population(s) of interest. The sample must be representative of the population — the sample must be:
- large enough to include the entire range of variability of the trait that occurs in the population, and
- random to avoid introducing any bias.
Thus, the greater the variability within the population, the larger the sample size that is required to accurately describe that population. (Throughout this and subsequent modules, you can generally assume that we’re referring to a representative sample, rather than a population.)
Statistics may be descriptive or analytical. [See Appendix B to briefly review some statistical terms and concepts].
Statistical Terms
The study of quantitative traits is sometimes referred to as “statistical genetics” because of its reliance on statistical methods. In order to understand the inheritance of quantitative characters and the methods applied to these characters, it is essential that you become familiar with fundamental statistics. A basic review is provided here.
When using symbols to represent these population parameters, it is important to distinguish between information about the population and that concerning a sample representing the population.
Similar Statistical Symbols
As a shorthand, statistics commonly use symbols to convey concepts. Often there are several symbols that relate to very similar, but slightly differing concepts. Here’s a list of symbols related to means, variance, and standard deviation that you will encounter in this lesson. The latter two parameters describe the variability or dispersion about the mean of the population or sample derived from a population.
Although the differences between these are important from a statistical perspective, they are commonly used synonymously.
| Parameter | For a population | For a fixed or selected sample of a population |
|---|---|---|
| Mean | [latex]\mu[/latex] or M | [latex]\bar{X}[/latex] |
| Variance | V or [latex]\delta^{2}[/latex] | [latex]s^{2}[/latex] |
| Standard deviation | [latex]\delta[/latex] | s |
Descriptive Statistics
Range — the lowest and highest phenotypic values in the population or sample for the character.
Mean (µ or M for population; [latex]\bar{X}[/latex] for sample) — describes the average performance of a random sample from a population for a trait. The mean is a measure of central tendency — it does not tell anything about the distribution of individual observations. Mean equals the sum of the trait values of each individual divided by the number of samples (n):
[latex]\bar{x} = \frac{\Sigma x}{n}[/latex]
Variance (V or σ2 for population; s2 for sample) — a measure of the scatter or dispersion of phenotypic values. The greater the variability among individuals, the greater the variance. Two populations with the same mean for the same character could differ greatly in their respective variance for that character.
Average the squared deviations from the mean, (X – X)2:
[latex]V = \sigma^{2} = \frac{\Sigma [(x - \bar{x})^{2}]}{n - 1}[/latex]
Standard deviation (σ for population; s for sample) — also a measure of dispersion around the mean. Standard deviation expresses the dispersion in the same unit as the mean.
Standard deviation is the square root of the variance.
[latex]\sigma = \sqrt{V} \text{ or } \sqrt{\sigma^{2}}[/latex]
A small variance and a small standard deviation tell us that the phenotypic values are near the mean value. In contrast, a large variance and standard deviation indicate that the trait values have a wide range.
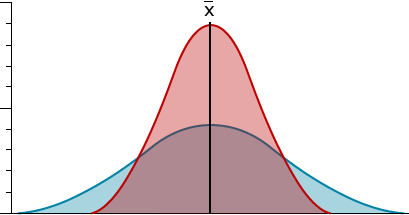
Samples in which the observations are clustered closely around the mean (red) have a smaller variance and standard deviation than observations dispersed widely (blue).
Coefficient of variation (CV) — the standard deviation as a percentage of the mean. Because the units cancel out, CV is a unitless measure.
Divide the standard deviation by the mean and multiply by 100:
[latex]CV = \frac{\sigma}{\bar{X}} \times 100[/latex]
A CV of about 10% or less is desirable in assessing biological systems. When the CV is greater than 10%, the variability in the sample or the population may be too great to sort out the factors contributing to that variability.
The mean and the variance are used to describe an individual characteristic, but plant breeders are frequently interested in more than one trait simultaneously. Two or more characteristics can vary together, and are thus not independent of one another.
Covariance provides measure of the strength of the correlation or dependent relationship between two or more sets of variables. When two traits are correlated, a change in one trait is likely to be associated with a change in the other trait. Variance is a special case of covariance that is the covariance of a variable with itself. Correlations between characteristics are measured by a correlation coefficient (r).
Covariance — the mean value of the product of the deviations of two random variables from their respective means. For example, the covariance of two random variables, x and y is expressed as:
[latex]Cov_{x,y} = \frac{\Sigma (x_{i} - \bar{x})(y_{i} - \bar{y})}{n - 1}[/latex]
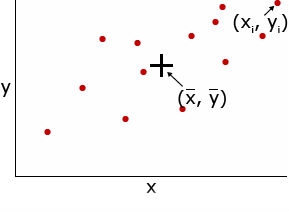
Correlation coefficient (r) — measures the interdependence of two or more variables and is obtained by dividing the covariance of x and y by the product of the standard deviations of x and y. The correlation coefficient can range from -1 to +1.
[latex]r = \frac{Cov_{x,y}}{S_{x}S_{y}}[/latex]
Correlation is a "scaled" version of covariance and the two parameters always have the same sign—positive, negative, or zero (0). When the sign is positive, the variables are positively correlated; when it's negative, they are said to be negatively correlated, and when it's zero, the variable are described as being uncorrelated. But it is important to note that a correlation between variables indicates that they are associated, but it does not imply a cause-and-effect relationship.
QTLs and Mapping
The relative importance of genetic and environmental factors for a given trait can be estimated by the phenotypic resemblance between relatives. Until recently, quantitative genetics focused on phenotypic information, but increasingly molecular biology tools are being applied in an effort to locate where quantitative trait loci (QTLs) occur in plant and animal genomes. Various genetic markers have been identified and mapped, allowing identification of QTLs by linkage analysis.
A common method for mapping QTLs is to cross two homozygous lines that have different alleles at many loci. The F1 progeny are then backcrossed and intercrossed to allow genes to recombine through independent assortment and crossing over. Offspring in segregating generations are examined for correlations between inheritance of marker alleles and phenotypes that are quantitatively inherited. QTL mapping will be covered in more detail in later courses on Molecular Genetics and Biotechnology and Molecular Plant Breeding.
Multiple Genes and Gene Action
The general types of gene action for quantitative characters (additive, full and partial dominance, and over-dominance) do not differ from those for qualitative traits. However, the genes contributing to the phenotype of a quantitative character may or may not differ in their individual gene action, and their relative effects on the trait’s expression may differ. Some may have major influence and others may have only minor effects on the phenotype. The genes controlling a quantitative trait may also interact. The table below gives examples of types of gene action at two loci. For quantitative traits this would be expanded to multiple loci.
| Gene Action or Interaction | Explanation | Example | ||
|---|---|---|---|---|
| Additive Effects | Genes affecting a genetic trait in a manner that each enhances the expression of the trait. | aabb = 0 | Aabb = 1 | aaBb = 1 |
| AAbb = 2 | AaBb = 2 | aaBB = 2 | ||
| AABb = 3 | AaBB = 3 | AABB = 4 | ||
| Dominance Effects | Deviations from additivity so the heterozygote is more like one parent than the other. With complete dominance, the heterozygote and the homozygote have equal effects | aabb = 0 | Aabb = 2 | aaBb = 2 |
| AAbb = 2 | AaBb = 4 | aaBB = 2 | ||
| AABb = 4 | AaBB = 4 | AABB = 4 | ||
| Interaction of Epistasis Effects | Two nonallelic genes (e.g., genes at different loci) may have no effect individually, yet have an effect when combined | aabb = 0 | Aabb = 0 | aaBb = 0 |
| AAbb = 0 | AaBb = 4 | aaBB = 0 | ||
| AABb = 4 | AaBB = 4 | AABB = 4 | ||
| Overdominance Effects | Each allele contributes a separate effect and the combined alleles contribute an effect greater than that of either allele separately | aabb = 0 | Aabb = 2 | aaBb = 2 |
| AAbb = 1 | AaBb = 4 | aaBB = 1 | ||
| AABb = 3 | AaBB = 3 | AABB = 2 | ||

In the preceding examples, A and B are assumed to have equal effects. However, this often may not be true because genes at different loci may affect the expression of the trait in different ways. Some QTLs may be genes with major effect, while others may contribute only a minor effect. Penetrance or expressivity (refer to Deviations from Expected Phenotypes in the “Gene Segregation and Genetic Recombination” module) may influence trait expression. Likewise, pleiotropic effects (refer to Gene Interactions in the “Gene Segregation and Genetic Recombination” module) may be present, affecting different traits in different ways.
Heritability
Conceptual Basis for Understanding Heritability
Heritability estimates the relative contribution of genetic factors to the phenotypic variability observed in a population. What causes variance among plants and among lines or varieties? Phenotypic variation observed among plants or varieties is due to differences in
- their genetic makeup,
- environmental influences on each plant or genotype, and
- interaction of the genotype and environment.
The effectiveness with which selection can be expected to take advantage of variability depends on how much of that variability results from genetic differences. Why? Only genetic effects can be transmitted to progeny. Heritability estimates
- the degree of similarity between parent and progeny for a particular trait, and
- the effectiveness with which selection can be expected to take advantage of genetic variability.
Family Resemblance
As mentioned in the introduction of this lesson, central to the understanding of quantitatively inherited traits is the recognition of family resemblance. Two relatives, such as a parent and its offspring, two full or half-siblings, or identical twins, would be expected to be phenotypically more similar to each other than either is to a random individual from a population. Although close relatives may share not only genes (they may also share similar environments for traits that have a large genetic component), resemblance between relatives is expected to increase as closer pairs of relatives are examined because they share more and more genes in common. In this conceptual framework, heritability can be understood as a measure of the extent to which genetic differences in individuals contribute to differences in observed traits.
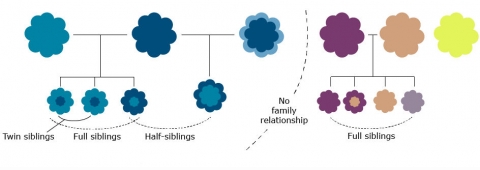
Statistical Basis for Understanding Heritability
For plant breeders, heritability can also be understood in a statistical framework by defining it as the proportion of the phenotypic variance that is explained by genetic variance. Heritability indicates the proportion of the total phenotypic variance attributable to genetic effects, the portion of the variance that is transmittable to offspring. A general formula for calculating heritability is
[latex]\text{Heritability} = \frac{V_{G}}{V_{P}}= \frac{V_{G}}{V_{G} + V_{E} + V_{GE}}[/latex]
[latex]=\frac{\sigma^{2}_g}{\sigma^{2}_{ph}} = \frac{\sigma^{2}_g}{\sigma^{2}_g + \sigma^{2}_c + \sigma^{2}_{ge}}[/latex]
where:
[latex]V_{P} = V_{G} + V_{E} + V_{GE}[/latex]
or
[latex]\sigma^{2}_{ph} = \sigma^{2}_{g} + \sigma^{2}_{e} + \sigma^{2}_{ge}[/latex]
and
[latex]V_{P} = \sigma^{2}_{ph}[/latex] = phenotypic variance (total variance of the population)
[latex]V_{G} = \sigma^{2}_{g}[/latex] = genotypic variance (variance due to genetic factors)
[latex]V_{E} = \sigma^{2}_{e}[/latex] = environmental variance (variance due to environmental factors)
[latex]V_{GE} = \sigma^{2}_{ge}[/latex] = genotype x environmental variance (variance due to interactions between genotypes and environmental factors)
Uses of Heritability Estimates
Heritability serves as a guide for making breeding decisions. It is generally used to
- determine the relative importance of genetic effects which could be transferred from parent to offspring
- determine which selection method would be most likely to improve the character
- predict genetic advance from selection
A key point to understand is that heritability is a population concept — application of heritability estimates is restricted to the population on which the estimate was based and to the environment in which the population was grown. However, some characters exhibit fairly consistent estimates (either high or low) among populations (within species) and environments. When considering characters that have high heritability, what we expect to observe for each genotype is that its phenotype will be quite predictable over a range of environments (growing conditions). In other words, for characters with high heritability, genotype fairly accurately predicts phenotype. This is not so for characters with low heritability.
Characters
Heritability depends on the range of typical environments experienced by the population under study (if the environment is fairly uniform, then heritability can be high, but if the range of environmental differences is high, then heritability may be low. Even when heritability is high, environmental factors may influence a characteristic. Heritability does not indicate anything about the degree to which genes determine a trait; instead it indicates the degree to which genes determine variation in a trait.
Characters having low heritabilities are usually highly sensitive to the environment, presenting greater breeding challenges — low heritability traits often require larger populations and more test environments than do characters having high heritabilities for selection and improvement.
| Heritability Estimate | Maize Characters |
|---|---|
| h2 < .70 |
|
| .50 < h2 < .70 |
|
| .30 < h2 < .50 |
|
| h2 < .30 |
|
Broad-Sense Heritability
Types of Heritability
There are two types of heritability: broad-sense and narrow-sense heritability.
Broad-Sense Heritability
Broad sense heritability, H2, estimates heritability on the basis of all genetic effects.
[latex]H^{2} = \frac{V_{G}}{V_{P}} \times 100[/latex]
[latex]= \frac{\sigma^{2}g}{\sigma^{2}_{ph}} \times 100[/latex]
It expresses total genetic variance as a percentage, and does not separate the components of genetic variance such as additive, dominance, and epistatic effects.
| Genetic variance | = | Additive variance | + | Dominance variance | + | Epistatic variance |
| VG | = | VA | + | VD | + | VI |
| [latex]\sigma^{2}_{e}[/latex] | = | [latex]\sigma^{2}_{A}[/latex] | + | [latex]\sigma^{2}_{D}[/latex] | + | [latex]\sigma^{2}_{I}[/latex] |
Generally, broad-sense heritability is a relatively poor predictor of potential genetic gain or breeding progress. Its usefulness depends on the particular population. Broad-sense heritability is
- more commonly used with asexually propagated crops than with sexually propagated agronomic crops
- applied to early generations of self-pollinated crops
Narrow-Sense Heritability
Narrow-sense heritability, h2, in contrast, expresses the percentage of genetic variance that is caused by additive gene action, VA.
[latex]h^{2} = \frac{V_{A}}{V_{P}} \times 100[/latex]
[latex]= \frac{\sigma^{2}_{A}}{\sigma^{2}_{ph}} \times 100[/latex]
Narrow-sense heritability is always less than or equal to broad-sense heritability because narrow-sense heritability includes only additive effects, whereas broad-sense heritability is based on all genetic effects.
The usefulness of broad- vs. narrow-sense heritability depends on the generation and reproductive system of the particular population. In general, narrow-sense heritability is more useful than broad-sense heritability since only additive gene action can normally be transmitted to progeny. This is, because in systems with sexual reproduction, only gametes (alleles) but not genotypes are transmitted to offspring. In contrast, in case of asexual reproduction, genotypes are transmitted to offspring.
| Broad-sense heritability | Narrow-sense heritability | |
|---|---|---|
| Symbols used | H2, H, hb2, or hB2 | h2, hn2, or hN2 |
| Predictor of Gain | Poor | Better |
| Genetic Variance | Additive, dominance, and epistatic | Additive only |
| Generation | Early | Later |
| Reproductive System | Self-pollinated or cloned population | Cross-pollinated |
Estimating Heritability
As the formulas presented above indicate, heritability is calculated from estimates of the components of phenotypic variation: genetic, environmental, and genetic x environmental interactions. Two main approaches are described here to help estimate the contribution of different G, E, and GxE components and for calculating heritability. One approach focuses on eliminating one or more variance component, while the other focuses on comparing the resemblance of parents and offspring. These estimates can be determined from an analysis of variance or regression analysis of the character performance of a population grown in several environments (multiple locations and/or years).
Testing a character’s performance in multiple environments (e.g., more than one location and/or years) is essential to get an accurate estimate of the environmental effects on the character. Test environments should be either random or representative of the target environment the type of environment for which the cultivar under development is intended. Heritability is based on variance, the average of the squared deviations from the mean—a statistical measure of how values vary from the mean. Testing in a single environment provides no measure of variance. The greater the number of environments used in the character’s evaluation, the better is the reliability of the variance estimate, as well as the heritability estimate. Without adequate testing in multiple environments, heritability estimates may be misleading.
When evaluating different genotypes for a specific character, if the genotypes vary widely in response to differing environments, environmental variance will be relatively high and heritability for the character low. Conversely, if the different genotypes perform in a similar manner across environments, e.g., certain genotypes are always among the best and others always the poorest regardless of environment, environmental variance will be low and heritability high.
Estimation Using Analysis of Variance (ANOVA)
Estimating heritability from an analysis of variance provides a way to measure the relative contributions of two or more sources of variability.
Several analytical procedures are commonly used to sort out the sources of variation in the sample, to determine the relationship among factors contributing to the variability, and to estimate the heritability of the character.
Analysis of Variance — this procedure identifies the relative contribution of the sources of observed variation in the sample. Sources of variation may include environment, replication, or genotypic effects. The portion of variation that cannot be attributed to known causes is called "error."
| Source of Variation | Expected Mean Squares |
|---|---|
| Genotypes | [latex]\sigma^{2}_{e} + r \sigma^{2}_{g}[/latex] |
| Error | [latex]\sigma^{2}_{e}[/latex] |
In this example, phenotypic variance is explained by differences in genetic composition, as well as to unknown factors. r stands for the number of replications.
[latex]\sigma^{2}_{ph} = \sigma^{2} + r \sigma^{2}_{g}[/latex]
The particular steps involved in this procedure and the analysis of variance table that results depend on the design of the experiment. Analysis of variance procedures and interpretation are discussed in the Quantitative Methods course.
Estimation using Parent-Offspring Regression
Heritability can also be estimated by evaluating the similarities between progeny and parent performance using regression analysis. This analysis is based on several assumptions.
- The particular character has diploid, Mendelian inheritance.
- There is no linkage among loci controlling the character of interest, or the population is in linkage equilibrium.
- The population is random mated.
- Parents are not inbred.
- There is no environmental correlation between the performance of parents and progeny (to avoid violating this last assumption, randomize parents and progeny within replications; i.e., do not test them in the same plot).
The linear regression model is:
[latex]Y_{i} = a + bX_{i} + e_{i}[/latex]
where:
- [latex]Y_{i}[/latex]= phenotypic value of progeny of the ith parent
- a = mean phenotypic value of all parents tested
- b = regression coefficient (slope of the line)
- [latex]x_{i}[/latex]= phenotypic value of the ith parent
- [latex]e_{i}[/latex]= experimental error in the measurement of Xi
Several analytical procedures are commonly used to sort out the sources of variation in the sample, to determine the relationship among factors contributing to the variability, and to estimate the heritability of the character.
Regression — this procedure examines the strength of the relationship between factors or the influence one factor has on another. The linear regression procedure fits a straight line to a scatterplot of data points. The general equation for the regression line is:
[latex]y = a + bx[/latex]
where:
- y = response or dependent variable
- x = predictor or independent variable
- a = y-intercept of the line
- b = regression coefficient, the slope of the line
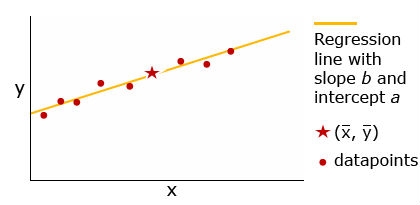
The regression line always passes through the point ([latex]\bar{x}, \bar{y}[/latex]). Relative to the total spread of the data, if most of the datapoints lie on or very near the line, there is a strong relationship between the predictor and response variables—x has a strong influence on y. In contrast, the fewer the points that fall on or near the line, the less influence x has on y. A cautionary note: although the x variable may have strong influence on the y variable, x may not be the cause of the y response, nor the sole factor influencing y.
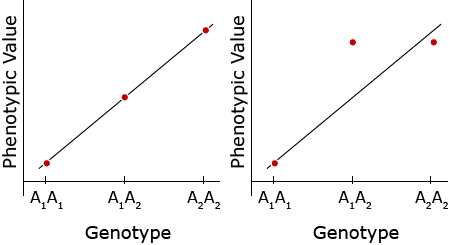
Regression can be used to assess the relative effect of environment on phenotypic value or to obtain information about gene action. The relative scatter about the regression line of a plot of genotype (the predictor variable, x) against phenotypic value (the response variable, y), provides information about gene action. For example, regression analysis of the following two examples suggests that the gene action in example 1 (left panel) is additive (no dominance), whereas there is a complete dominance (by the A2 allele) in the case of example 2 (right panel) (Fehr, 1987).
When the heterozygous genotype has a value midway between the two homozygotes and thus all three genotypic values fall on the linear regression line the only gene action contributing to the phenotype is additive.
Regression analysis of phenotypic values of progeny (y) against parents (x) provides useful information about the degree of similarity of progeny to the parents.
Alternative Formula
An alternative formula for calculating the regression coefficient, b, is
[latex]b = \frac{\Sigma(X - \bar{X})(Y - \bar{Y})}{\Sigma (X - \bar{X})^{2}}[/latex]
where:
- b = regression coefficient
- X = parent values
- Y = progeny values
The performance of the progeny is a function of the genetic factors inherited from the parents. (Assume that “parent” means either a random plant or line from a population.) Thus, X, the parent value, is the independent variable, and Y, the progeny value, is the response or dependent variable.
Regression Coefficient
What does the regression coefficient, b, tell us?
If b = 1, then
- gene action is completely additive,
- negligible environmental effect,
- and negligible experimental error.
The smaller the value of b, the less closely the progeny resemble their parent(s), indicating
- greater environmental influence on the character,
- greater dominance and/or epistatic effects, and/or
- greater experimental error.
An analysis of variance will provide estimates of the relative influence of genetics, environment, and experimental error.
The type of heritability and the specific formula used to estimate it depends on the type of progeny evaluated.
Types of Progeny
The population’s reproductive mode and mating design determine the type of heritability and the formula used to calculate the estimate.
Selfed progeny
- F2 plants are self-pollinated to obtain the F3. All the alleles in the F3 come from the F2 parent. Evaluate the character performance of the F3
- Regress the performance of the F3 on the performance of their F2 parents.
- The regression coefficient, b, is equal to H2, broad-sense heritability because its genetic variance includes dominance, additive, and epistatic effects.
[latex]H^{2} = b \times 100[/latex] - Since it is difficult to obtain information about gene action (dominance, epistasis, additive) in self-pollinated populations, narrow-sense heritability is a poor predictor of genetic gain and rarely used in these populations. Inbreeding causes an upward bias in the heritability estimate.
Full-sib progeny
- Two random F2 plants are mated. Half of the alleles in the F3 come from one parent and half from the other. Evaluate the character performance of the F3.
- Determine the mid-parent value of the two parents. Mid-parent value, X = (x1 + x2) /2
- Regress the progeny on the mid-parent value. The regression of progeny on the mid-parent value is
[latex]\frac{ \frac{1}{2} V_A}{\frac{1}{2} V_P} = \frac{ \frac{1}{2} \sigma^2 _A}{\frac{1}{2} \sigma_{ph}} = \frac{\sigma^2_A}{\sigma^2_{ph}}[/latex]
Since the progeny have both parents in common, only additive variance is included, so the regression coefficient, b, is equal to narrow-sense heritability.
[latex]h^{2} = b \times 100[/latex]
Half-sib progeny
- Open-pollinate F2 plants. Seed will be harvested from each F2 individual separately. Progenies from the same F2 plant have the maternal parent (the respective F2 plant) in common, while the paternal parent is pollen from the whole F2 population. Thus all offspring from an F2 plant after open pollination are "half-sibs".
- Regress the performance of the half-sib progenies on their parents.
[latex]b = \frac{\sigma^{xy}}{\sigma^{2}_{x}}[/latex]
where:
[latex]\sigma^{xy}[/latex] = covariance between parents, x, and their progeny, y
[latex]\sigma^{2}_{x}[/latex] = phenotypic variation among parents - The covariance between parents and progeny includes additive variance and some forms of additive epistasis (usually negligible), but no dominance variance. Thus, narrow-sense heritability can be estimated. The regression coefficient, b, is equal to half the heritability value.
- Multiply the regression coefficient by 2 to obtain narrow-sense heritability.
[latex]h^{2} = 2b \times 100[/latex]

Heritability Influences
Heritability is not an intrinsic property of a trait or a population. As we've seen, it is influenced by:
- population — generation, reproductive system, and mating design
- environment — locations and/or years
- experimental design — experimental unit (plant, plot, etc.), replication, cultural practices, techniques for data gathering.
Heritability can be manipulated by increasing the number of replicates and number of environments sampled (in space and/or time). Genetic variance can be increased by using diverse parents and by increasing the selection intensity. Heritability is only an indicator to guide the breeder in making selections and is not a substitute for other considerations, such as breeding objectives and resource availability.
Genetic Advance from Selection
Evolution
Estimating Response to Selection
Evolution can be defined as genetic change in one or more inherited trait that takes place over time within a population or group of organisms. Plant breeders can use quantitative genetics to predict the rate and magnitude of genetic change. The amount and type of genetic variation affects how fast evolution can occur if selection is imposed on a phenotype.
The amount that a phenotype changes in one generation is called the selection response, R. The selection response is dependent on two factors—the narrow-sense heritability and the selection differential, S. The selection differential is a measure of the average superiority of individuals selected to be parents of the next generation.
[latex]R = h^{2}S[/latex]
The above equation is often called the “breeder’s equation”. It shows the key point that response to selection increases when either the heritability of the trait or the strength of the selection increases.
Realized Heritability
In an experiment, the observed response to selection allows the calculation of an estimate of the narrow-sense heritability, often called the realized heritability. A low h2 (<0.01) occurs when offspring of the selected parents differ very little from the original population, even though there may be a large difference between the population as a whole and the selected parents. Conversely, a high h2 (> 0.6) occurs when progeny of the selected parents differ from the original population almost as much as the selected parents.
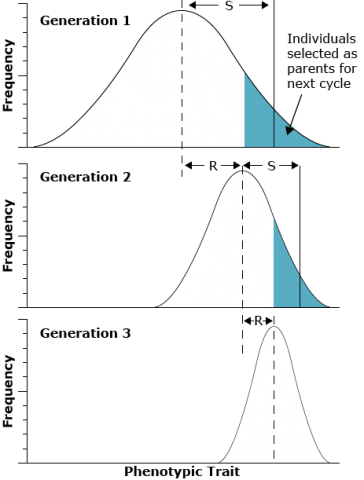
In the figure in the next screen, it can be seen that the selection differential (S) in each generation is the difference between the mean of the entire original population and the mean of group of individuals selected to form the next generation. In contrast, the response to selection (R) indicates the differences in population means across generations. The value of R is the difference between the mean of the offspring from the selected parents and the mean of the entire original population:
[latex]S = \bar{T}_{S} - \bar{T}[/latex]
[latex]R = \bar{T}_{O} - \bar{T}[/latex]
where:
- T = mean of the entire original population
- TS = mean of selected parents
- TO = mean of the offspring of the selected parents
Adaptive Value
The proportionate contribution of offspring of an individual to the next generation is referred to as fitness of the individual. Fitness is also sometimes called the adaptive value or selective value. Note in the figure that the non-selected members of the population do not contribute to the next generation and that selection over time reduced the variance of the population.
Types of Selection
Artificial selection refers to selective breeding of plants and animals by humans to produce populations with more desirable traits. Artificial selection is typically directional selection because it is applied to individuals at one extreme of the range of variation for the phenotype selected. This type of selection process is also called truncation selection because there is a threshold phenotypic value above which the individuals contribute and below which they do not. In contrast, under natural selection in non-managed populations, other types of selection may occur.
Three main types of selection are generally recognized. All three operate under natural selection in natural populations, whereas under artificial selection via selective breeding by humans only directional selection is common.
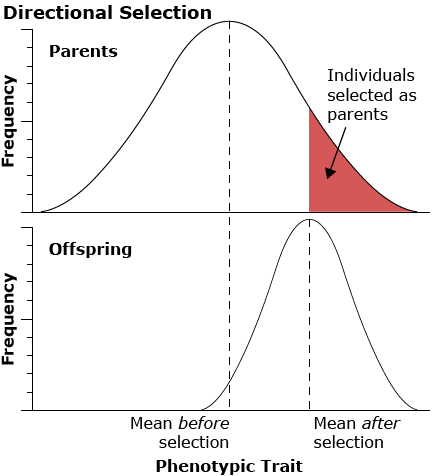
Directional Selection
Directional selection acts on one extreme of the range of variation for a particular characteristic.
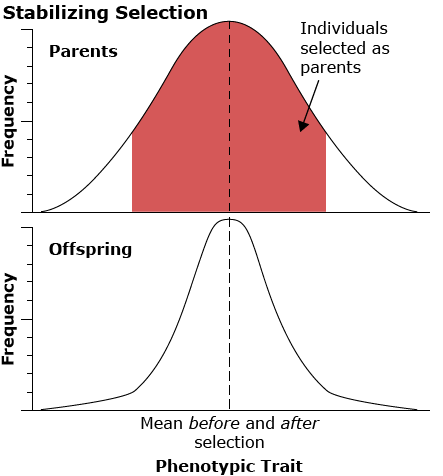
Stabilizing selection
Stabilizing selection works against the extremes in the distribution of the phenotype in the population. An example of this type of selection is human birth weight. Infants of intermediate weight have a much higher survival rate than infants who are either too large or too small.
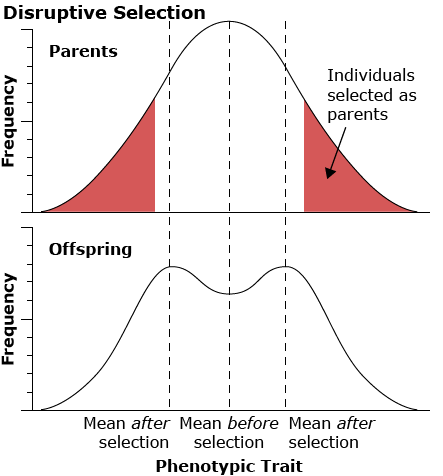
Disruptive selection
Disruptive selection favors the extremes and disfavors the middle of the range of the phenotype in the population.
Genetic Advance from Selection
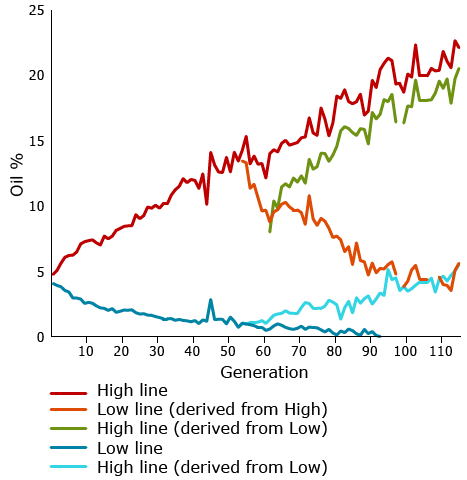
One of the most famous longest-term selection experiments is a study conducted by University of Illinois geneticists who have been selecting maize continuously for over 100 generations since 1896. They have been changing oil and protein content in separate experiments, selecting for either high or low content. In some cases after multiple generations, they have shifted selection from high to low or vice versa.
Expected Gain From Selection
Because resources are limited, the breeder's objective is to carry forward as few plants or lines as possible without omitting desirable ones. How does the breeder decide how many and which plants or lines within a population to carry forward to the next generation? The breeder can use heritability estimates to predict the probability that selecting a given percentage of the population or selection intensity, i, will result in progress. The expected progress or gain can be calculated using this formula:
[latex]G_C = (k) (\sqrt{V_P})(h^2) = k \sigma_{ph} h^2[/latex]
where:
- Gc = expected gain or predicted genetic advance from selection per cycle
- k = selection intensity — a constant based on the percent selected and obtained from statistical tables (note that some people use hte i symbol instead of k for selection intensity
- [latex]\sqrt{V_{p}}[/latex] or [latex]\sigma_{ph}[/latex] = square root of phenotypic variance (equivalent to standard deviation)
- h2 = narrow - sense heritability in decimal form (narrow - sense is used for sexually reproduced populations whenever possible, and broad sense heritability, H2, is used for self - pollinating and asexually reproduce populations)
Caution: The phenotypic values must exhibit a normal, or bell-curve, distribution for Gc to be valid
| % | k |
|---|---|
| 1 | 2.67 |
| 2 | 2.42 |
| 5 | 2.06 |
| 10 | 1.76 |
| 20 | 1.40 |
| 50 | 0.80 |
| 90 | 0.20 |
| 100 | 0 |
As long as the distribution of phenotypic values is normally distributed, selection intensity values (symbolized by k or sometimes i) can be found in statistical tables. The intensity of selection practiced by plant or animal breeders depends just on the proportion of the population in the selected group.
The selection intensity is a standardized selection differential and is a measure of the superiority of the individuals selected as parents for breeding relative to the population from which they were selected. Representative values of k are shown in the table.
For Your Information
As will be explained in the next section, a key statistic used to describe populations is the mean performance of the population of genotypes. The mean performance of a population can be described by a combination of values for performance of both homozygous and heterozygous genotypes, as well as the relative frequency of alleles.
For illustration using a locus with two alleles, A1 and A2, the genotypic value of the homozygotes is designated as A1A1 =+a and A2A2 = -a, while the heterozygous genotype is A1A2 = d.
The value of a is the performance of a homozygous genotype minus the average performance of the two homozygous genotypes.
[latex]+a = A_1A_1 - \frac{(A_1A_1 + A_2A_2)} {2} [/latex]
[latex]-a = A_2A_2 - \frac{(A_1A_1 = A_2A_2)}{2}[/latex]
The value of d measures the degree of dominance between alleles, and is the difference between the value of the heterozygote and the mean of the homozygotes.
[latex]d = A_1A_2 - \frac{(A_1A_1 + A_2 A_2)}{2}[/latex]
space
Examples of relative genotypic values are given here in depictions showing a and d under different types of gene action.
| Gene Action | Degree of Dominance | Relative Genotypic Values |
|---|---|---|
| Additive | 0 | 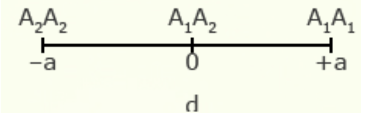 |
| Complete dominance | 1 | 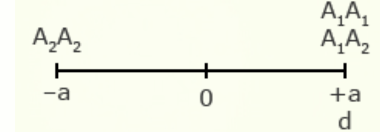 |
| Partial dominance | 3/4 | 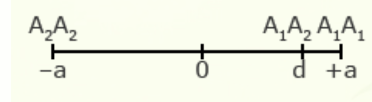 |
| Partial dominance | 1/2 | 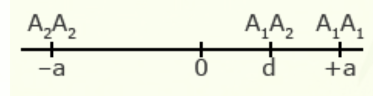 |
| Overdominance | 2 | 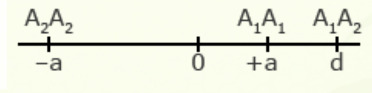 |
The difference between the depictions of partial dominance show an example of how the effect of an allele can vary depending on whether the locus is a major gene or minor. Remember, additivity of genetic effects for quantitative traits does not mean that there are equal effects of all alleles at a locus or all loci affecting the trait.
The study of quantitative traits is sometimes referred to as “statistical genetics” because of its reliance on statistical methods. In order to understand the inheritance of quantitative characters and the methods applied to these characters, it is essential that you become familiar with fundamental statistics. A basic review is provided here.
When using symbols to represent these population parameters, it is important to distinguish between information about the population and that concerning a sample representing the population.
Populations can be characterized by the amount and type of genetic variability contained within them. Genetic improvement of a quantitative character is based on effective selection among individuals that differ in what is known as the genotypic value. Variation among the genotypic values represents the genotypic variance of a population.
The genotypic value is the phenotype exhibited by a given genotype averaged across environments. A related concept is the breeding value, which is the portion of the genotypic value that determines the performance of the offspring. Genotypic value is property of the genotype and therefore is a concept that describes the value of genes to the individual, whereas breeding value describes the value of genes to progeny and therefore helps us understand how a trait is inherited and transmitted from parents to offspring . Remember that only additive genetic effects can be passed on to progeny. Non-additive genetic effects and environmental effects cannot be inherited by offspring.
References
Barbour, M.G, J.H. Burk, F.S. Gilliam, W.D. Pitts and M.W. Schwartz. 1999. Terrestrial Plant Ecology. 3rd edition. Benjamin Cummings, San Francisco, CA.
Clausen, J., D.D. Keck, and W. Hiesey. 1940. Experimental studies on the nature of species. I. Effects of varied environments on western North American plants. Carnegie Inst. Wash. Publ. 520.
Clausen, J., D. D. Keck, and W. M. Hiesey. 1948. Experimental studies on the nature of species. III. environmental responses of climactic races of Achillea. Carnegie Inst. Wash. Publi. 581.
Conner, J.K. and D.L. Hartl. 2004. A Primer of Ecological Genetics. Sinauer Associates, Sunderland, MA.
Falconer, D.S., and T.F.C. Mackay. 1996. Introduction to Quantitative Genetics. 4th edition. Longman Publ. Group, San Francisco, CA.
Hallauer, A. R. and J. B. Miranda. 1988. Quantitative Genetics in Maize Breeding. 2nd Edition. Iowa State University Press, Ames, IA.
Hill, W.G. 2005. A century of corn selection. Science 307: 683-684.
Pierce, B. A. 2008. Genetics: A Conceptual Approach. 3rd edition. W.H. Freeman, New York.
Rausher, M.D.. 2005. Example of Clausen, Keck, and Hiesey Experiment, Lecture 1-Lineages, Populations, and Genetic Variation. Online lecture notes from course on Principles of Evolution.
Department of Crop Science, University of Illinois at Urbana-Champaign. Values obtained for protein in the strains selected for oil and the values for oil obtained for the strains selected for protein each generation (1896-2004). 2007.
(1) Genetic potential of an organism.
(2) Genetic makeup of an individual.
(1) A genotype that contains one dominant and one recessive gene or two different co-dominant genes (Aa,bB,CD).
(2) An individual that has two copies of the same allele at a locus, e.g., AA or aaa or AAAA.
A line resulting from pre-breeding.

Introduction
Mutations
Mutations are the ultimate source of all genetic variation. Mutations can occur at all levels of genetic organization, classified mainly as either chromosome mutations or genome mutations. Chromosome mutations are discussed in this module. Chromosome alterations involve either single nucleotides or fragments of chromosomes and are either small-scale (one or a few nucleotides substituted, inserted, or deleted) or large-scale (deletions, insertions, inversions, or translocations involving large segments of chromosomes or duplications of entire genes). Genome mutations—involving changes in number of whole chromosomes or sets of chromosomes—will be covered separately in the module on Ploidy—Polyploidy, Aneuploidy, Haploidy.
Genetic variation—dissimilarity between individuals attributable to differences in genotype—that is generated by mutations is acted upon by various evolutionary forces. Evolutionary processes that alter species and populations include selection, gene flow (migration), and genetic drift—whether or not plants are cultivated or wild. Evolution can be defined as a change in gene frequency over time. The way that plants evolve is dependent on both genetic characteristics and the environment they face.
Genetic variation results from differences in DNA sequences and, within a population, occurs when there is more than one allele present at a given locus. Major processes that affect heritable variation in crop plants are topics emphasized throughout the lessons of this course. Changes in gene frequencies within populations caused by natural selection can lead to enhanced adaptation, while changes caused by human-directed selection can facilitate the development of useful genetic variability and selection of superior genotypes. Selection is the differential reproduction of the products of recombination—both within and between chromosomes.
Genetic Resources
Historically plant breeders seeking sources of variability were constrained in choice of parental materials or plant genetic resources that were interfertile within closely related gene pools. But a range of new techniques such as mutagenesis, genetic engineering (transgenic or transformed plants), and in vitro methods (tissue culture, doubled haploids, induced polyploids) expand the source and scope of variability that can be used in crop improvement.
Our expanding understanding of the molecular basis of genetics has provided insights and technologies that further not only our basic understanding of genes and their regulation, but also provide additional tools for crop improvement. Molecular techniques enable breeders to generate genetic variability, transfer genes between unrelated species, move synthetic genes into crops, and make selections at the molecular, cellular, or tissue levels. Combining these laboratory techniques with conventional field approaches can shorten the time required to develop new or improved cultivars. The importance and application of molecular technologies are rapidly increasing.
These topics mentioned above—mutations, gene expression, genetic markers, sources of genetic variation, genetic engineering, and molecular breeding methods—will be briefly mentioned in this module, but covered in greater detail in the later courses including Plant Breeding Methods, Molecular Genetics, and Biotechnology and Molecular Plant Breeding.
- Recognize how mutations are classified and inherited, as well as how mutations affect structure, processes, and products of genes and chromosomes.
- Understand the basic principles of transcription and translation.
- Become familiar with sources of genetic variation for cultivated plants, including crop gene pools and genetic engineering methods.
Mutations as Heritable Change
Without heritable variation, any trait favored by selection will not be passed on to offspring. Mutation is defined as heritable change in genetic information. Mutations entail modification of the nucleotide sequence of DNA and consist of any permanent alteration of a DNA molecule that can be passed on to offspring. DNA is a highly stable molecule and it replicates with a high degree of accuracy. However changes in DNA structure and replication errors can occur. Mutation involves modifications in the sequence of bases in DNA transmitted through mitosis and meiosis.
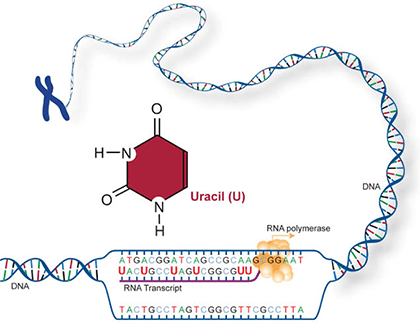
A nucleotide consists of a sugar molecule (ribose in RNA or deoxyribose in DNA) attached to phosphate group and a nitrogen-containing base. In DNA or RNA molecules, each strand has a backbone of sugar and phosphate groups (Fig. 17).
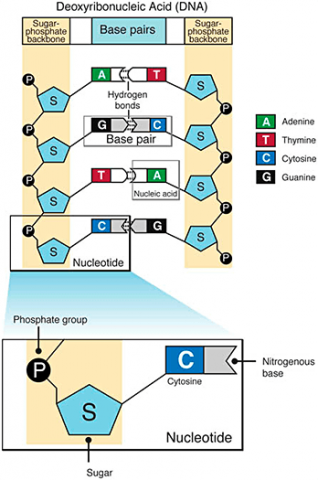
CHEMICAL BASES IN DNA AND RNA
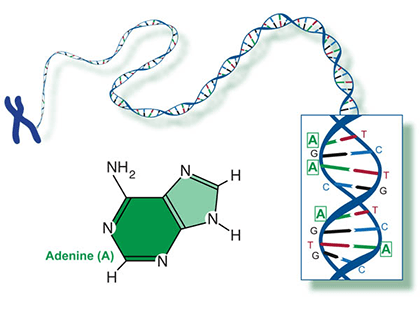
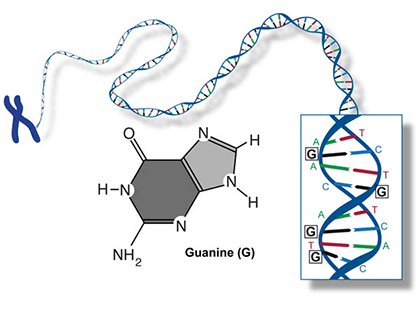
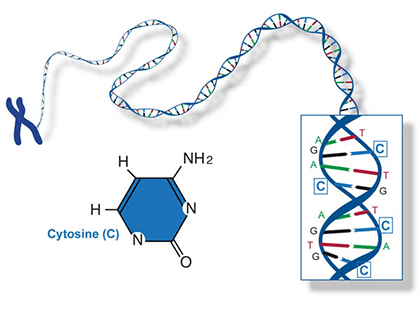
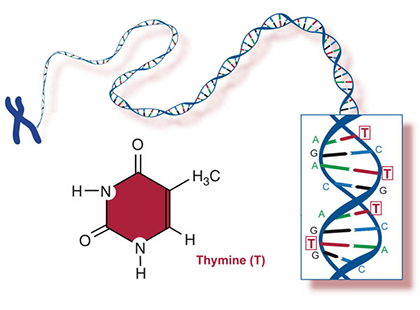
Two of the four nitrogenous bases in DNA—adenine (Fig. 13) and guanine (Fig. 14) are known as purines and the other two—cytosine (Fig. 15) and thymine (Fig. 16) are pyrimidines. Adenine, guanine, and cytosine are also found in RNA. Another pyrimidine known as uracil (Fig. 17) is the base used in RNA in place of thymine.
Some mutations occur in loci that encode for gene products such as proteins, and thus they may affect the processes of transcription, translation, or gene expression—processes that happen during the creation of proteins from the genetic code in DNA. But mutations also can occur in parts of the genome that do not code for any gene products (called noncoding DNA) or sequences that serve to control regulatory functions in the cell or chromosomes. For most loci, mutation changes allelic frequencies at a very slow rate and therefore consequences are negligible. Mutations may or may not change the phenotype of an organism. The majority of mutations that do occur are neutral in their effect and therefore do not have an influence on fitness. Some mutations are beneficial. But mutations can have deleterious effects, causing disorders or death.
Amino acids are a set of 20 different molecules used to build proteins. A peptide is one or more amino acids linked by chemical bonds (termed peptide bonds). Linked amino acids form chains of polypeptides (Fig. 18). The amino acid sequences of proteins are encoded in genes.
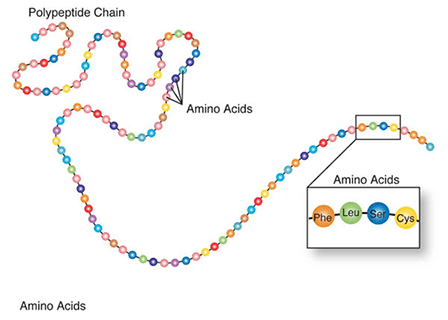
One or more polypeptides form the building blocks of proteins (Fig. 19). Proteins perform a variety of roles in cells.
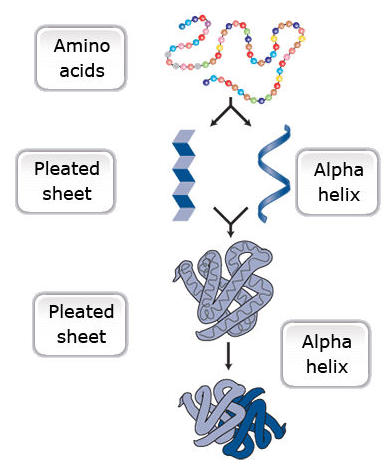
Primary protein structure is a sequence of a chain of amino acids.
Secondary protein structure occurs when the sequence of amino acids is linked by hydrogen bonds.
Tertiary protein structure occurs when certain attractions are present between alpha helices and pleated sheets.
Quaternary protein structure is a protein consisting of more than one amino acid chain
Types of Mutations
Classification of Mutations
Mutations can occur at all levels of genetic organization, ranging from simple base nucleotide pair alterations to shifts and rearrangements in sequences of nucleotides along fragments of chromosomes to changes in the number and structure of whole chromosomes.
A mutation is a change from one hereditary state to another, e.g., allele A mutates to allele a. For a given locus, the normal allele is referred to as the ‘wildtype’. Mutations are usually recessive and therefore their effects are hidden in heterozygotes. There are a number of common ways to classify mutations, including the following:
- causal agent
- rate or frequency of occurrence
- kind of tissue involved and its type of inheritance
- impact on fitness or function, or
- molecular structure and scale of the mutation.
Spontaneous vs. Induced Mutations
Depending on the cause, mutations can be either spontaneous or induced:
- Spontaneous mutations occur naturally with no intentional exposure to a mutagen. Spontaneous mutations can result from copying errors made during cell division.
- Induced mutations are caused by mutagens, either chemicals or radiation.
RARE VS. RECURRENT MUTATIONS
Recall from the module on Population Genetics, mutational events in a population can be classified into two categories based on frequency of occurrence:
Rare mutations (also called non-recurrent mutations) are defined as those that occur infrequently in populations. Rare mutations are usually recessive and occur in a heterozygous condition so that their effect on the phenotype is not apparent. Rare mutations will usually be lost from populations due to random genetic drift.
Recurrent mutations are defined as those that occur repeatedly and thus can possibly cause a change in gene frequency in populations. For a given locus, the rate of allele A mutating to allele a can be given as the frequency u per generation; a mutates to A at a rate v:
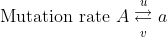
With the frequency of A symbolized as p and that of a symbolized as q, then at equilibrium, pu = qv, or q = p/(u + v) (see the Equation below).
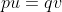
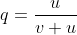
Mutation Rates
Falconer and Mackay (1996) summarize the following key points about mutation rates and their frequency in populations:
- normal spontaneous mutations alone can produce only very slow changes of allele frequency;
- mutation rates are generally quite low for most loci in most organisms, occurring about 10-5 to 10-6 per generation or, stated another way, about 1 in 100,000 to 1 in 1,000,000 gametes carry a newly mutated allele at any locus;
- with respect to equilibrium in both directions (u and v) in natural populations, forward mutation (from wildtype to mutant; u) is much more frequent than reverse mutation (from mutant to wildtype; v); and
- an equilibrium state known as the mutation-selection balance can maintain deleterious alleles at low frequency; selection acts to eliminate deleterious recessive alleles, but very slowly when the allele frequency is low; even if the elimination process of selection is slow, an equilibrium occurs if mutation creates new copies of the deleterious allele.
Somatic vs. Germinal Mutations
Plants are multicellular organisms, but mutation typically starts from a single cell. There are two broad categories of mutations that are classified according to the type of cell tissue involved:
- Somatic mutations occur in somatic tissue, which does not produce gametes. Somatic cells divide by mitosis and therefore through that process, mutations can be passed on to daughter cells. Somatic mutations may have no effect on the phenotype if their function is covered by that of normal cells. However somatic cells that stimulate rapid cell division are the basis for tumors in plants and animals. Somatic mutations usually occur as single events (typically in a single cell) in multicellular organisms or organs that lead to chimera, which is a part of a plant with a genetically different constitution as compared to other parts of the same plant. Somatic mutations are not transmitted to progeny (Fig. 1).
- Germinal or germ-line mutations occur in reproductive cells that produce gametes, and therefore can be passed on to future generations. Germ cells or gametes are formed by meiosis. If a germinal mutation is inherited, then it can be carried in all of the somatic and germ-line cells of the offspring (Fig. 1).
Effects of Mutation on Fitness or Function
Mutations can affect fitness in various ways and can therefore be classified based on their effect on individual fitness:
- Deleterious mutations are those that are harmful and have a negative effect on phenotype, decreasing the fitness of the individual.
- Advantageous mutations are those that are beneficial and have a positive or desirable effect on phenotype, increasing the fitness of the individual.
- Neutral mutations have neither beneficial nor harmful effects.
- Lethal mutationsare detrimental and lead to the death of the organism when present.
Mutations can also be classified by their effect on gene function:
- Loss-of-function mutations either result in a gene product that has less function or one that has no function. Phenotypes associated with loss-of-function mutations are usually recessive. Many of the mutations that are associated with crop domestication from wild progenitors involve loss-of-function alleles (Gepts 2002).
- Gain-of-function mutations result in a gene product that has novel function. Altered phenotypes associated with gain-of-function mutations are usually dominant. Many of the changes in crop plants brought about by genetic engineering involve gain-of-function mutations (Gepts 2002).
However, it is important to underscore that not all mutations occur in genes or protein-coding regions of the chromosome, nor do all mutations that do occur in genes lead to altered proteins.
Point vs. Chromosomal Mutations
Mutations are often divided into those that affect a single gene, termed a gene mutation—also sometimes called a point mutation—and those that affect the structure of chromosomes, called a chromosomal mutation. These latter two classes of mutations will be covered in more detail after the concept of gene expression is introduced in the following section.
Point Mutation
Point or Gene Mutation
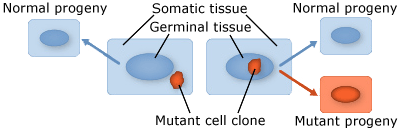
A point mutation is when a single base pair (or just a few) is altered (Fig. 2), an alteration at a “micro” level. There are two general types of point mutations: substitutions or insertions and deletions (the latter two are collectively called INDELs).
- Base pair substitutions involve an alteration of a single nucleotide in the DNA. A substitution mutation can entail either a transition or a transversion:
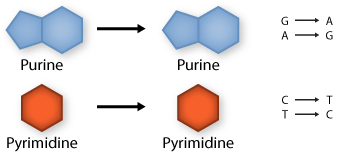
Transition: purine replaced by a different purine or pyrimidine by a different pyrimidine 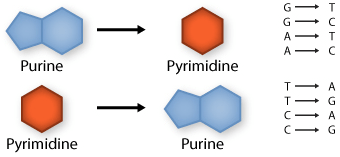
Transversion: purine replaced by a pyrimidine or pyrimidine by a purine
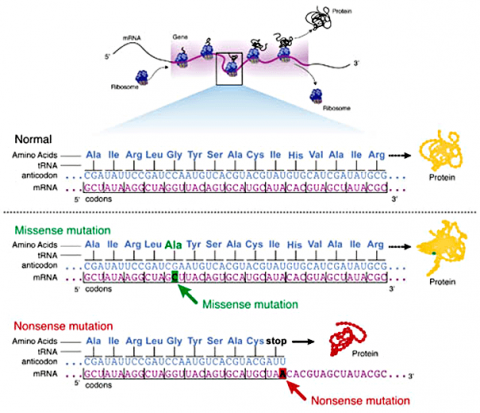
Missense Mutations
Some substitution mutations have no effect on the protein coded for. One reason is because of the redundancy of the genetic code (recall that about one fourth of all base pair substitutions code for the same amino acid; such mutations are termed silent mutations since there is no change in amino acid that results from the substitution). Another reason for lack of effect is that even if a change in amino acid occurs (termed missense mutation), it may have no actual influence on the function of a protein (Fig. 3). Also any mutation located within a non-coding region of the chromosome will not be translated into a protein. Lastly, an altered gene may be masked by other normal copies of the gene present in the genome.
In certain cases, point mutations can have a significant effect—particularly when a substitution produces a stop codon so that the alteration causes the protein synthesis to halt before the protein is entirely translated, altering the entire structure. These are called nonsense mutations (Fig. 3).
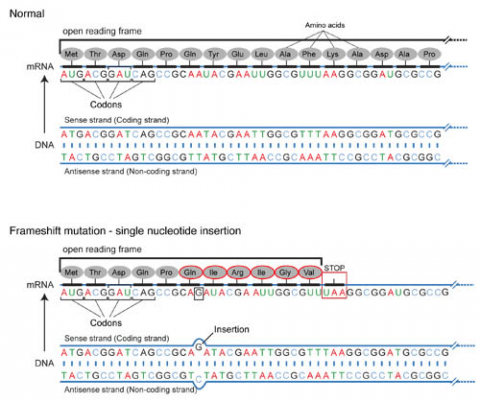
Frameshift Mutation
Base pair insertions and deletions are additions (INDELs) or losses of one to several nucleotide pairs in a gene (Fig. 2). Mutations that are insertions and deletions tend to have a much greater effect than do mutations that are base pair substitutions because they disrupt the normal reading frame of trinucleotides. Recall that each group of three bases corresponds to one of 20 different amino acids used to build a protein. Mutations involving base pair insertions and deletions are often therefore referred to as frameshift mutations. Under these circumstances the DNA sequence following the mutation is read incorrectly (Fig. 4).
Chromosomal Mutation
MUTATIONS INVOLVING CHROMOSOME SEGMENTS
Different cells of the same organism and different individuals of the same species generally have the same number of chromosomes, and homologous chromosomes are typically uniform in number and in the arrangement of genes along them. However, mutations can occur that alter the number or structure of chromosomes.
Changes involving chromosomal rearrangements entail the following basic types: deletions, duplications, insertions, inversions, substitutions, and translocations—alterations that occur at a “macro” level (Fig. 5).
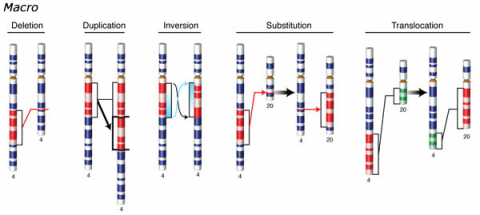
- Chromosomal deletions are when loss of a chromosome segment occurs.
- Chromosomal duplications occur when a chromosome segment is present more than once in a genome or along an individual chromosome (Fig. 5). Mutations of this type can involve duplication of chromosome fragments of either noncoding regions or genes that do code for a protein or other gene product. Gene duplications have been important events in the evolution of many crop plants, for example in cotton.Both chromosome deletions and duplications generally result from unequal crossing over during meiosis, whereby one gamete receives a chromosome with a duplicated segment or gene and the other gamete receives a chromosome with a missing or "deleted" segment.
- Chromosomal inversions happen when two breaks occur in a chromosome and the broken segment turns 180°—reversing the orientation of the sequence—and then reattaches (Fig. 5). Such inverted segments may or may not involve the centromere (termed pericentric inversion vs. paracentric inversion). A consequence of chromosomal inversions is that they either prevent crossing over or if crossing over occurs, the recombinants may be eliminated during meiosis. During meiosis, inverted chromosome segments may form loops in order to pair with the same (non-inverted) sequence on homologous chromosomes.
- Chromosomal insertions (not pictured) and chromosomal substitutions are when gain of an extra fragment of chromosome occurs (Fig. 5).
- Chromosomal translocations entail a change in the location of a chromosome segment. Commonly translocations are reciprocal and thus result from exchange of segments between two non-homologous chromosomes (Fig. 5).
Transpositions
Chromosome segments can also be translocated to a new location on the same chromosome or to a different chromosome but without reciprocal exchange; both of the latter types of mutations are termed transpositions. A transposon (also called a transposable element) is a DNA element that can move from one location to another. These mobile DNA sequences commonly occur in some genomes and can themselves cause other mutations to occur, depending on where they "transpose".
Discussion
Mutants and mutations are best known in the context of horror films. In the context of plant breeding and more generally crop production, discuss the consequences of mutations—are they good or bad? Which kinds of mutations are desirable and which ones are undesirable?
Sources of Variation
Sources of Genetic Variability
Plant breeding is dependent on differential phenotypic expression. Loci with only one allelic variant (homozygosity) in a breeding population have no effect on the phenotypic variability. Variation can be introduced to breeding populations by various methods:
- hybridization and recombination by sexual reproduction within or between species or populations
- genetic transformation or genetic engineering using recombinant DNA methods
- induced or spontaneous mutations and transposable elements (transposons)
- chromosome manipulation via change in chromosome number and structure (ploidization) [to be discussed in the module on Ploidy—Polyploidy, Aneuploidy, Haploidy]
- tissue or cell culture techniques [to be discussed in the module on Ploidy—Polyploidy, Aneuploidy, Haploidy]
CONCEPT OF CROP GENE POOLS
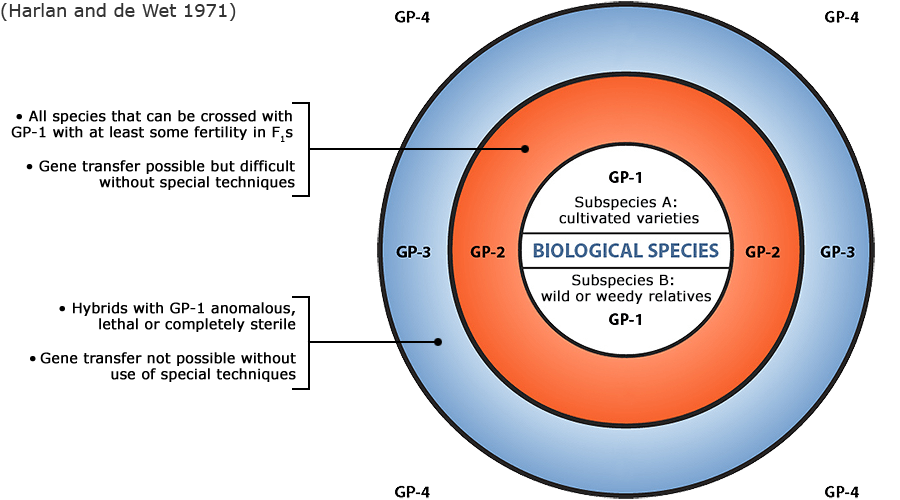
Plant germplasm is a term used to refer to an individual, group of individuals or a clone that represents a genotype, population, or species. With reference to a given crop and its wild and cultivated relatives, the concept of gene pool (all of the genes shared by individuals in a group of interbreeding individuals) has been applied to categorize a broad range of plant genetic resources according to the ease of gene transfer or gene flow to the particular crop species (Harlan and de Wet 1971).
Gene Pools
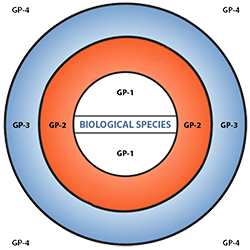
Figure 6 depicts three main categories in the original scheme outlined by J. R. Harlan and J.M.J. de Wet (1971) defined as:
- primary gene pools (GP-1, consisting of biological species that can be intercrossed easily without problems of fertility in the progeny; including both cultivated varieties and wild progenitors of the crop),
- secondary gene pools (GP-2, consisting of more distant relatives that can be intercrossed with difficulty and result in diminished fertility in the hybrids and later generations; including both cultivated and wild relatives of the crop), and
- tertiary gene pools (GP-3, consisting of very distant relatives that can be hybridized with the crop only with special techniques, e.g., embryo rescue, due to problems such as sterility, lethality and other abnormalities),
With the addition of a fourth gene pool that contains synthetic variants and lines with nucleic acid sequences that do not normally occur in nature. Methods of genetic engineering relevant to this fourth gene pool category will be covered briefly in the next section of this module. Examine a more detailed view of the gene pool concept.
Genetic Engineering
Plant Transformation
GENETIC ENGINEERING AND PLANT TRANSFORMATION
Genetic engineering, also referred to as recombinant DNA or rDNA technology or gene splicing, involves moving a DNA segment from one organism into another to 'transform' the recipient or host. Through a broad range of techniques encompassing biotechnology (for example, gene manipulation, gene transfer, cloning of organisms), novel genetic diversity can be generated that extends beyond species boundaries or can be designed and synthesized de novo in molecular laboratories. Potentially, any gene from any species, as well as synthesized segments, could be transferred into a plant using genetic engineering.
Gene transfer can be applied for a variety of objectives:
- Add different or new functions
- Alter existing traits—amplify, suppress, or prevent the expression of a gene already present in the recipient's genome
- 'Tag' and isolate genes in the recipient plant
- Tool for basic gene regulation and developmental studies
Requirements for Gene Transfer
In order to efficiently generate transformants (plants that possess DNA introduced via recombinant DNA technologies), the transformation system used must satisfy several requirements.
- Ability to get DNA into host cells in high concentration to increase the probability of incorporation into the host genome
- Incorporation into the host nucleus (or chloroplast if the objective is to minimize gene flow by pollen or to produce a large quantity of therapeutic proteins)
- Integration into host genome (or stabilization as an autonomous replicon—a plasmid or minichromosome)
- The introduced gene is expressed and translated properly
GENERAL STEPS
- Identification and isolation of a gene that confers a desired trait.
- Introduce the gene into a suitable construct and carrier, such as plasmids or bacterial vectors, for delivery into the host.
- Introduce the DNA into the host.
- Identify and select transformants.
- Regenerate plants.
- Assay for expression of the trait.
- Test for normal sexual transmission, or asexual propagation, of the transferred gene.
The carrier that will deliver the DNA into the host should have certain features.
- Sites in which to insert passenger DNA sequences (gene of interest, plus a selectable marker gene if the gene of interest does not allow for easy selection of transgenic plants).
- Sequences to mediate integration into the host genome
- Selectable marker gene for identification and selection of transformants
Usually, the DNA sequence to be transferred into the host is joined with other sequences to facilitate transfer, incorporation, and expression of the gene. Here's a generalized construct for a T-DNA vector, a carrier derived from an Agrobacterium tumefaciens plasmid (Fig. 1).
The original version of this chapter contained H5P content. You may want to remove or replace this element.
Fig. 1 Diagram of a DNA construct
Introduce the DNA
Several methods are available to introduce the DNA into the host.
- Vector-mediated transfer
- Direct DNA uptake—DNA cannot be taken directly into cells having a cell wall so protoplast must be used.
- Microinjection—DNA is injected directly into the host nucleus
- Acceleration of DNA—coated particles - particles are "shot" into the cell (particle bombardment or gene gun)
Genetic transformation plays an important role in modern-day crop improvement. The first transgenic plant was created in 1983. By 1996, there were already 1.7 million hectares of genetically modified (GM) crops and this number increased 100-fold to 170 million by 2012 and is still increasing. The majority of the GM crops (soybean, corn, cotton, papaya, canola and sugarbeet) were created by the use of Agrobacterium tumefaciens (vector-mediated transfer) to resist either herbicides or insects. Herbicide-resistant crops greatly simplified weed management where mechanization in agriculture is high. Insect-resistant crop plants produce stable yields. The tremendous expansion of GM crop production, however, is not realized without controversies. There is currently an intense public debate over the impact of GM crops on human and animal health. Besides health issues, other concerns surrounding GM crops are whether they can create superweeds by crossing to related weeds, become invasive or cause unintended harm to wildlife.
Bt Gene: Vector Constructs
Let's follow the transfer of a Bt gene into a plant.
The Bt gene was identified and isolated from Bacillus thuringiensis, a bacterium. The gene produces a protein that has toxic effects on Diptera (flies), Lepidoptera (butterflies and moths), and Coleoptera (beetles) species. Soybean was transformed using Agrobacterium tumefaciens. Two different T-DNA vector constructs carrying the Bt gene and one control construct were tested for effectiveness in transforming soybean cells and expressing the Bt toxin (Fig. 7).

Bt Gene: Transformation
Leaf disks from soybean plants were infected and cultured on selective (+) and control (-) media—the selective medium was gradually enriched with an antibiotic (Fig. 8). At time 1, the leaf disks were infected with the respective constructs. Conditions were used to promote callus production and growth. At time 2, the plates were evaluated for calli formation.

The original version of this chapter contained H5P content. You may want to remove or replace this element.
Transformed cells are able to develop into calli. These are selected and transferred to a medium containing both antibiotics and growth regulators that promote the formation of shoots and roots (Fig. 9).
Bt Gene: Insect Resistance Evaluation
Plantlets are regenerated and transferred to pots containing sterilized soil. Nearly all of the regenerated plants exhibited normal morphology and vigor. A few had chlorophyll deficiencies— these were eliminated from the study. The remaining regenerated plants were evaluated for insect resistance. An equal number of insect larvae are placed on each regenerated plant; plants are isolated to prevent insects from moving among plants.


Bt Gene: Insect Resistance Data Analysis
After several days, the dead larvae on each plant are counted. Here are the data.
| Gene Construct | No. of Plants Showing % Larvae Mortality | |||
| < 25 % | 25% - 50% | 51% - 75% | 76% - 100% | |
| Intact | 14 | 7 | 0 | 0 |
| Fusion | 2 | 6 | 2 | 20 |
| Control | 29 | 0 | 0 | 0 |
Study the information in the above table. Look for any patterns in the data. Interpret the data by selecting all of the true statements
The original version of this chapter contained H5P content. You may want to remove or replace this element.
Advantages and Disadvantages
Although recombinant DNA technologies have some problems, the technologies offer several advantages.
| Advantages | Disadvantages |
|---|---|
| Characters can be transferred from divergent species without the limitation of sexual compatibility | Difficult to identify and isolate gene |
| Single gene or gene sets can be transferred into important breeding lines without the deleterious effects of linked genes. | Insertion is random |
| Transferred character ordinarily exhibits dominant, single-gene inheritance | Difficult to obtain proper expression |
| Still must screen at whole plant level and under normal production conditions | |
| Expensive |
Despite its limitations, plant transformation has additional advantages over conventional breeding. Millions of cells, with regeneration capacity, can be screened for the desired trait in a few weeks. A desired gene can be transferred without the necessity of generations of breeding to move the trait from one line into another. Recombinant DNA technology can also be used to place synthetic genes into plant genomes.
The insertion point of the transferred gene cannot be controlled. Plants contain an estimated 500,000 to 5,000,000 kilobases (kb) of DNA. The maize genome, for example, has more than 4,000,000 kb. Generally, transferred DNA involves relatively small amounts of DNA, on the order of 10 kb, so the insertion ordinarily has little effect on chromosome pairing, recombination, or mitosis. The incorporated gene may or may not affect other genes in the recipient genome, depending on where it inserts.
- In a non-coding region—no effect on the recipient genome
- In a gene that occurs in multiple copies in the genome—the effect, if any, is usually not detectable.
- In a single-copy gene—inactivates or alters the expression of the single-copy gene.
Insertion into a single copy gene is rare. If it does insert into a single-copy gene, inactivation or alteration of the expression of the disrupted gene may be undetected, or may cause favorable or adverse results—albino and other chlorophyll deficiencies are common problems.
Why do these characters generally exhibit dominant, single-gene inheritance? Traits acquired via gene transfer often add a function to the transformed plant. Because the transferred trait is unique in the transformant's genome, the transformant does not possess any contrasting alleles for the character. Thus, its inheritance is expected to be dominant and as a single gene.
The original version of this chapter contained H5P content. You may want to remove or replace this element.
Gene transfer is also used to suppress or eliminate, or to amplify the expression of genes already possessed by the host plant. These are also usually designed to behave as dominants.
Expression involves many steps, all of which must occur properly to obtain the desired phenotype. Expression must be appropriately regulated.
- Generation of the gene's product-requires proper transcription, mRNA processing, and translation.
- Location of expression must be in the appropriate plant part.
- Timing of expression needs to occur at the right stage of the plant's development.
- Amount needs to be at an effective level or extent of expression to generate the desired phenotype.
Reflection
The Module Reflection appears as the last "task" in each module. The purpose of the Reflection is to enhance your learning and information retention. The questions are designed to help you reflect on the module and obtain instructor feedback on your learning. Submit your answers to the following questions to your instructor.
- In your own words, write a short summary (< 150 words) for this module.
- What is the most valuable concept that you learned from the module? Why is this conceptvaluable to you?
- What concepts in the module are still unclear/the least clear to you?
References
Collard, B.C.Y., M.Z.Z. Jahufer, J.B. Brouwer, and E.C.K. Pang. 2005. An introduction to markers, quantitative trait loci (QTL) mapping and marker-assisted selection for crop improvement: the basic concepts. Euphytica 142: 169-196.
Falconer, D.S. and T.F.C. Mackay. 1996. Introduction to Quantitative Genetics. 4th edition. Longman Pub. Group, Essex, England.
Harlan, J.R., and J.M.J de Wet. 1971. Towards a rational classification of cultivated plants. Taxon 20: 509-517.
Gepts, P. 2002. A comparison between crop domestication, classical plant breeding, and genetic engineering. Crop Science 42: 1780-1790.
Nageswara-Rao, M. and J.R. Soneji. 2008. Molecular genetic markers: what? why? which one for exploring genetic diversity? Perspectives-The Science Advisory Board, 8 September 2008 [available online September 23, 2011, http://www.scienceboard.net/community/perspectives.210.html].
Neuffer, M.G, E.H. Coe, and S.R. Wessler. 1997. Mutants of Maize. Cold Springs Harbor Laboratory Press.
NIH-NHGRI (National Institutes of Health. National Human Genome Research Institute). 2011. Talking Glossary of Genetic Terms. [available online February 6, 2017, http://www.genome.gov/glossary/].
For Your Information
Amino acids are the building blocks of polypeptides, proteins, and enzymes. The order of the nucleotides on a strand of RNA, as transcribed from DNA, determines the order of amino acids in a polypeptide. Each group of three consecutive nucleotides of the RNA codes for a particular amino acid, or the beginning or end of the message. These triplets of nucleotides are called codons (Fig. 20).

The genetic code, or instructions from a gene that direct the cell to make a specific protein, is usually based on the messenger RNA (mRNA) sequence (Fig. 21). In mRNA, uracil (U), rather than thymine (T), is the nucleotide base that complements adenine (A) on the DNA strand; guanine (G) complements cytosine (C) in both DNA and RNA.
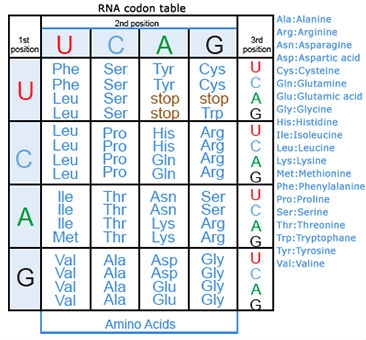
Here are some examples of codons:
- A-A-A and A-A-G signal the amino acid lysine (Lys)
- G-A-A and G-A-G code for glutamine (Gln)
- A-U-G signals the start of a coding sequencing and codes for methionine (Met)
- U-A-A, U-A-G, and U-G-A are stop codons.
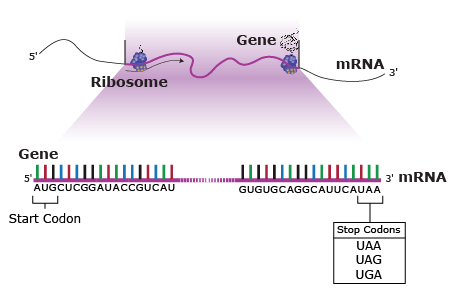
Of the 64 possible combinations of three bases, 61 specify an amino acid, while the remaining three combinations are stop codons, or trinucleotide sequences that indicate the end of the message, terminate translation of that mRNA section, and signal a “stop” to protein synthesis (Fig. 22).
The portion of a DNA molecule that, when translated into amino acids, contains no stop codons is referred to as an open reading frame (Fig. 23).
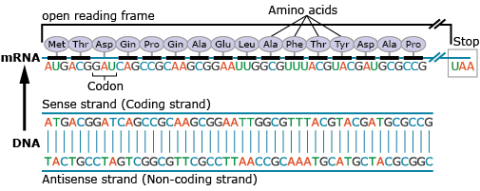
Acknowledgements
This module was developed as part of the Bill & Melinda Gates Foundation Contract No. 24576 for Plant Breeding E-Learning in Africa.
Crop Genetics, Mutations and Variation - Authors: Laura Merrick, Arden Campbell, Deborah Muenchrath, and Shui-Zhang Fei (ISU)
Multimedia Developers: Gretchen Anderson, Todd Hartnell, and Andy Rohrback (ISU)
How to cite this module: Merrick, L., A. Campbell, D. Muenchrath, and S. Fei. 2016. Mutations and Variation. In Crop Genetics, interactive e-learning courseware. Plant Breeding E-Learning in Africa. Retrieved from https://pbea.agron.iastate.edu
A type of reproductive cell that leads to the production of gametes. In plants, male germ cells are contained within pollen grains and female germ cells are contained within ovules.
This is the question that is trying to be proven incorrect. Usually, this occurs when trying to prove some treatment causes a significant difference from expected. Opposite of alternative hypothesis.
Self-pollination in plants.
Enzymes are organic catalysts. They cause chemical reactions to occur rapidly which would otherwise occur very slowly or not at all. Most of them are very specific— for example, urease catalyzes the hydrolysis of urea. Many enzymes require a metallic cofactor to work with them. Also, enzymes are large complex of globular proteins consisting of one or more polypeptide chains.