APPENDIX A: Right Triangle Trigonometry
Trigonometric Identities
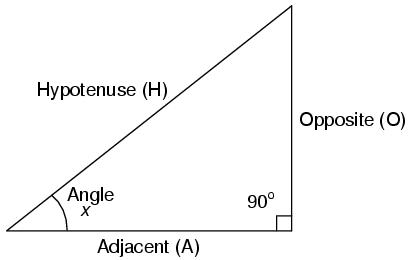
[latex]Sin x\:=\frac{O}{H}[/latex]
[latex]Cos x\:=\frac{A}{H}[/latex]
[latex]Tan x\:=\frac{O}{A}[/latex]
[latex]Tan x\:=\frac{Sin x}{Cosx}[/latex]
[latex]csc x\:=\frac{H}{O}[/latex]
[latex]sec x\:=\frac{H}{A}[/latex]
[latex]cot x\:=\frac{A}{O}[/latex]
[latex]cot x\:=\frac{Cosx}{Sinx}[/latex]
H is the Hypotenuse, always being opposite the right angle. Relative to angle x, O is the Opposite and A is the Adjacent. “Arc” functions such as “arcsin”, “arccos”, and “arctan” are the complements of normal trigonometric functions. These functions return an angle for a ratio input. For example, if the tangent of 45o is equal to 1, then the “arctangent” (arctan) of 1 is 45o. “Arc” functions are useful for finding angles in a right triangle if the side lengths are known.
The Pythagorean Theorem
[latex]H^2 =A^2 +O^2[/latex]
