4 ALTERNATING CURRENT
4.1 What is Alternating Current (AC)?
Alternating Current
Most students of electricity begin their study with what is known as direct current (DC), which is electricity flowing in a constant direction, and/or possessing a voltage with constant polarity. DC is the kind of electricity made by a battery (with definite positive and negative terminals), or the kind of charge generated by rubbing certain types of materials against each other.
Alternating Current vs Direct Current
As useful and as easy to understand as DC is, it is not the only “kind” of electricity in use. Certain sources of electricity (most notably, rotary electromechanical generators) naturally produce voltages alternating in polarity, reversing positive and negative over time. Either as a voltage switching polarity or as a current switching direction back and forth, this “kind” of electricity is known as Alternating Current (AC):
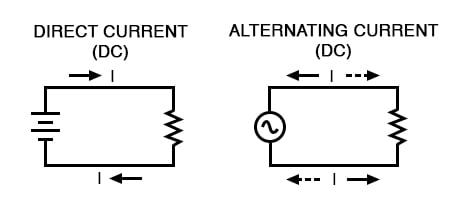
Whereas the familiar battery symbol is used as a generic symbol for any DC voltage source, the circle with the wavy line inside is the generic symbol for any AC voltage source.
One might wonder why anyone would bother with such a thing as AC. It is true that in some cases AC holds no practical advantage over DC. In applications where electricity is used to dissipate energy in the form of heat, the polarity or direction of current is irrelevant, so long as there is enough voltage and current to the load to produce the desired heat (power dissipation). However, with AC it is possible to build electric generators, motors and power distribution systems that are far more efficient than DC, and so we find AC being used predominantly across the world in high power applications. To explain the details of why this is so, a bit of background knowledge about AC is necessary.
AC Alternators
If a machine is constructed to rotate a magnetic field around a set of stationary wire coils with the turning of a shaft, AC voltage will be produced across the wire coils as that shaft is rotated, in accordance with Faraday’s Law of electromagnetic induction. This is the basic operating principle of an AC generator, also known as an alternator:

Notice how the polarity of the voltage across the wire coils reverses as the opposite poles of the rotating magnet pass by. Connected to a load, this reversing voltage polarity will create a reversing current direction in the circuit. The faster the alternator’s shaft is turned, the faster the magnet will spin, resulting in an alternating voltage and current that switches directions more often in a given amount of time.
While DC generators work on the same general principle of electromagnetic induction, their construction is not as simple as their AC counterparts. With a DC generator, the coil of wire is mounted in the shaft where the magnet is on the AC alternator, and electrical connections are made to this spinning coil via stationary carbon “brushes” contacting copper strips on the rotating shaft. All this is necessary to switch the coil’s changing output polarity to the external circuit so the external circuit sees a constant polarity:

The generator shown above will produce two pulses of voltage per revolution of the shaft, both pulses in the same direction (polarity). In order for a DC generator to produce constant voltage, rather than brief pulses of voltage once every 1/2 revolution, there are multiple sets of coils making intermittent contact with the brushes. The diagram shown above is a bit more simplified than what you would see in real life.
The problems involved with making and breaking electrical contact with a moving coil should be obvious (sparking and heat), especially if the shaft of the generator is revolving at high speed. If the atmosphere surrounding the machine contains flammable or explosive vapors, the practical problems of spark-producing brush contacts are even greater. An AC generator (alternator) does not require brushes and commutators to work, and so is immune to these problems experienced by DC generators.
AC Motors
The benefits of AC over DC with regard to generator design are also reflected in electric motors. While DC motors require the use of brushes to make electrical contact with moving coils of wire, AC motors do not. In fact, AC and DC motor designs are very similar to their generator counterparts (identical for the sake of this tutorial), the AC motor being dependent upon the reversing magnetic field produced by alternating current through its stationary coils of wire to rotate the rotating magnet around on its shaft, and the DC motor being dependent on the brush contacts making and breaking connections to reverse current through the rotating coil every 1/2 rotation (180 degrees).
Transformers
So we know that AC generators and AC motors tend to be simpler than DC generators and DC motors. This relative simplicity translates into greater reliability and lower manufacturing cost. But what else is AC good for? Surely there must be more to it than design details of generators and motors! Indeed there is. There is an effect of electromagnetism known as mutual induction, whereby two or more coils of wire placed so that the changing magnetic field created by one induces a voltage in the other. If we have two mutually inductive coils and we energize one coil with AC, we will create an AC voltage in the other coil. When used as such, this device is known as a transformer:
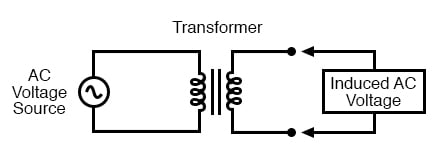
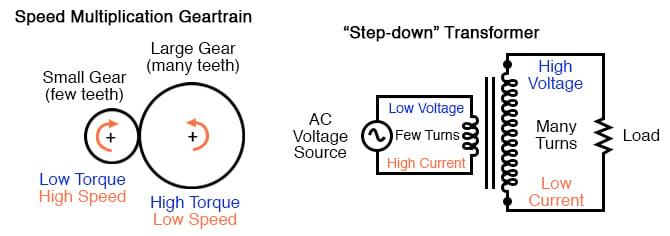
The fundamental significance of a transformer is its ability to step voltage up or down from the powered coil to the unpowered coil. The AC voltage induced in the unpowered (“secondary”) coil is equal to the AC voltage across the powered (“primary”) coil multiplied by the ratio of secondary coil turns to primary coil turns. If the secondary coil is powering a load, the current through the secondary coil is just the opposite: primary coil current multiplied by the ratio of primary to secondary turns. This relationship has a very close mechanical analogy, using torque and speed to represent voltage and current, respectively:

If the winding ratio is reversed so that the primary coil has less turns than the secondary coil, the transformer “steps up” the voltage from the source level to a higher level at the load:
The transformer’s ability to step AC voltage up or down with ease gives AC an advantage unmatched by DC in the realm of power distribution in figure below. When transmitting electrical power over long distances, it is far more efficient to do so with stepped-up voltages and stepped-down currents (smaller-diameter wire with less resistive power losses), then step the voltage back down and the current back up for industry, business, or consumer use.
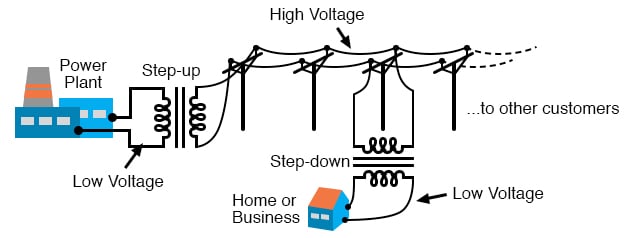
Transformer technology has made long-range electric power distribution practical. Without the ability to efficiently step voltage up and down, it would be cost-prohibitive to construct power systems for anything but close-range (within a few miles at most) use.
As useful as transformers are, they only work with AC, not DC. Because the phenomenon of mutual inductance relies on changing magnetic fields, and direct current (DC) can only produce steady magnetic fields, transformers simply will not work with direct current. Of course, direct current may be interrupted (pulsed) through the primary winding of a transformer to create a changing magnetic field (as is done in automotive ignition systems to produce high-voltage spark plug power from a low-voltage DC battery), but pulsed DC is not that different from AC. Perhaps more than any other reason, this is why AC finds such widespread application in power systems.
- DC stands for “Direct Current,” meaning voltage or current that maintains constant polarity or direction, respectively, over time.
- AC stands for “Alternating Current,” meaning voltage or current that changes polarity or direction, respectively, over time.
- AC electromechanical generators, known as alternators, are of simpler construction than DC electromechanical generators.
- AC and DC motor design follows respective generator design principles very closely.
- A transformer is a pair of mutually-inductive coils used to convey AC power from one coil to the other. Often, the number of turns in each coil is set to create a voltage increase or decrease from the powered (primary) coil to the unpowered (secondary) coil.
- Secondary voltage = Primary voltage (secondary turns / primary turns)
- Secondary current = Primary current (primary turns / secondary turns)
4.2 Measurements of AC Magnitude
Measurements of AC Magnitude
So far we know that AC voltage alternates in polarity and AC current alternates in direction. We also know that AC can alternate in a variety of different ways, and by tracing the alternation over time we can plot it as a “waveform.” We can measure the rate of alternation by measuring the time it takes for a wave to evolve before it repeats itself (the “period”), and express this as cycles per unit time, or “frequency.” In music, frequency is the same as pitch, which is the essential property distinguishing one note from another.
However, we encounter a measurement problem if we try to express how large or small an AC quantity is. With DC, where quantities of voltage and current are generally stable, we have little trouble expressing how much voltage or current we have in any part of a circuit. But how do you grant a single measurement of magnitude to something that is constantly changing?
Ways of Expressing the Magnitude of an AC Waveform
One way to express the intensity, or magnitude (also called the amplitude), of an AC quantity is to measure its peak height on a waveform graph. This is known as the peak or crest value of an AC waveform:

Another way is to measure the total height between opposite peaks. This is known as the peak-to-peak (P-P) value of an AC waveform:

Unfortunately, either one of these expressions of waveform amplitude can be misleading when comparing two different types of waves. For example, a square wave peaking at 10 volts is obviously a greater amount of voltage for a greater amount of time than a triangle wave peaking at 10 volts. The effects of these two AC voltages powering a load would be quite different:

One way of expressing the amplitude of different wave shapes in a more equivalent fashion is to mathematically average the values of all the points on a waveform’s graph to a single, aggregate number. This amplitude measurement is known simply as the average value of the waveform. If we average all the points on the waveform algebraically (that is, to consider their sign, either positive or negative), the average value for most waveforms is technically zero, because all the positive points cancel out all the negative points over a full cycle:

This, of course, will be true for any waveform having equal-area portions above and below the “zero” line of a plot. However, as a practical measure of a waveform’s aggregate value, “average” is usually defined as the mathematical mean of all the points’ absolute values over a cycle. In other words, we calculate the practical average value of the waveform by considering all points on the wave as positive quantities, as if the waveform looked like this:

Polarity-insensitive mechanical meter movements (meters designed to respond equally to the positive and negative half-cycles of an alternating voltage or current) register in proportion to the waveform’s (practical) average value, because the inertia of the pointer against the tension of the spring naturally averages the force produced by the varying voltage/current values over time. Conversely, polarity-sensitive meter movements vibrate uselessly if exposed to AC voltage or current, their needles oscillating rapidly about the zero mark, indicating the true (algebraic) average value of zero for a symmetrical waveform. When the “average” value of a waveform is referenced in this text, it will be assumed that the “practical” definition of average is intended unless otherwise specified.
Another method of deriving an aggregate value for waveform amplitude is based on the waveform’s ability to do useful work when applied to a load resistance. Unfortunately, an AC measurement based on work performed by a waveform is not the same as that waveform’s “average” value, because thepower dissipated by a given load (work performed per unit time) is not directly proportional to the magnitude of either the voltage or current impressed upon it. Rather, power is proportional to the square of the voltage or current applied to a resistance (P = E2/R, and P = I2R). Although the mathematics of such an amplitude measurement might not be straightforward, the utility of it is.
Consider a bandsaw and a jigsaw, two pieces of modern woodworking equipment. Both types of saws cut with a thin, toothed, motor-powered metal blade to cut wood. But while the bandsaw uses a continuous motion of the blade to cut, the jigsaw uses a back-and-forth motion. The comparison of alternating current (AC) to direct current (DC) may be likened to the comparison of these two saw types:

The problem of trying to describe the changing quantities of AC voltage or current in a single, aggregate measurement is also present in this saw analogy: how might we express the speed of a jigsaw blade? A bandsaw blade moves with a constant speed, similar to the way DC voltage pushes or DC current moves with a constant magnitude. A jigsaw blade, on the other hand, moves back and forth, its blade speed constantly changing. What is more, the back-and-forth motion of any two jigsaws may not be of the same type, depending on the mechanical design of the saws. One jigsaw might move its blade with a sine-wave motion, while another with a triangle-wave motion. To rate a jigsaw based on its peak blade speed would be quite misleading when comparing one jigsaw to another (or a jigsaw with a bandsaw!). Despite the fact that these different saws move their blades in different manners, they are equal in one respect: they all cut wood, and a quantitative comparison of this common function can serve as a common basis for which to rate blade speed.
Picture a jigsaw and bandsaw side-by-side, equipped with identical blades (same tooth pitch, angle, etc.), equally capable of cutting the same thickness of the same type of wood at the same rate. We might say that the two saws were equivalent or equal in their cutting capacity. Might this comparison be used to assign a “bandsaw equivalent” blade speed to the jigsaw’s back-and-forth blade motion; to relate the wood-cutting effectiveness of one to the other? This is the general idea used to assign a “DC equivalent” measurement to any AC voltage or current: whatever magnitude of DC voltage or current would produce the same amount of heat energy dissipation through an equal resistance:

How is Root Mean Square (RMS) Relevant to AC?
In the two circuits above, we have the same amount of load resistance (2 Ω) dissipating the same amount of power in the form of heat (50 watts), one powered by AC and the other by DC. Because the AC voltage source pictured above is equivalent (in terms of power delivered to a load) to a 10 volt DC battery, we would call this a “10 volt” AC source. More specifically, we would denote its voltage value as being 10 volts RMS. The qualifier “RMS” stands for Root Mean Square, the algorithm used to obtain the DC equivalent value from points on a graph (essentially, the procedure consists of squaring all the positive and negative points on a waveform graph, averaging those squared values, then taking the square root of that average to obtain the final answer). Sometimes the alternative terms equivalent or DC equivalent are used instead of “RMS,” but the quantity and principle are both the same.
RMS amplitude measurement is the best way to relate AC quantities to DC quantities, or other AC quantities of differing waveform shapes, when dealing with measurements of electric power. For other considerations, peak or peak-to-peak measurements may be the best to employ. For instance, when determining the proper size of wire (ampacity) to conduct electric power from a source to a load, RMS current measurement is the best to use, because the principal concern with current is overheating of the wire, which is a function of power dissipation caused by current through the resistance of the wire. However, when rating insulators for service in high-voltage AC applications, peak voltage measurements are the most appropriate, because the principal concern here is insulator “flashover” caused by brief spikes of voltage, irrespective of time.
Instruments Used to Measure the Amplitude of a Waveform
Peak and peak-to-peak measurements are best performed with an oscilloscope, which can capture the crests of the waveform with a high degree of accuracy due to the fast action of the cathode-ray-tube in response to changes in voltage. For RMS measurements, analog meter movements (D’Arsonval, Weston, iron vane, electrodynamometer) will work so long as they have been calibrated in RMS figures. Because the mechanical inertia and dampening effects of an electromechanical meter movement makes the deflection of the needle naturally proportional to the average value of the AC, not the true RMS value, analog meters must be specifically calibrated (or mis-calibrated, depending on how you look at it) to indicate voltage or current in RMS units. The accuracy of this calibration depends on an assumed waveshape, usually a sine wave.
Electronic meters specifically designed for RMS measurement are best for the task. Some instrument manufacturers have designed ingenious methods for determining the RMS value of any waveform. One such manufacturer produces “True-RMS” meters with a tiny resistive heating element powered by a voltage proportional to that being measured. The heating effect of that resistance element is measured thermally to give a true RMS value with no mathematical calculations whatsoever, just the laws of physics in action in fulfillment of the definition of RMS. The accuracy of this type of RMS measurement is independent of waveshape.
Relationship of Peak, Peak-to-Peak, Average, and RMS
For “pure” waveforms, simple conversion coefficients exist for equating Peak, Peak-to-Peak, Average (practical, not algebraic), and RMS measurements to one another:

In addition to RMS, average, peak (crest), and peak-to-peak measures of an AC waveform, there are ratios expressing the proportionality between some of these fundamental measurements. The crest factor of an AC waveform, for instance, is the ratio of its peak (crest) value divided by its RMS value. The form factor of an AC waveform is the ratio of its RMS value divided by its average value. Square-shaped waveforms always have crest and form factors equal to 1, since the peak is the same as the RMS and average values. Sinusoidal waveforms have an RMS value of 0.707 (the reciprocal of the square root of 2) and a form factor of 1.11 (0.707/0.636). Triangle- and sawtooth-shaped waveforms have RMS values of 0.577 (the reciprocal of square root of 3) and form factors of 1.15 (0.577/0.5).
Bear in mind that the conversion constants shown here for peak, RMS, and average amplitudes of sine waves, square waves, and triangle waves hold true only for pure forms of these waveshapes. The RMS and average values of distorted waveshapes are not related by the same ratios:

This is a very important concept to understand when using an analog D’Arsonval meter movement to measure AC voltage or current. An analog D’Arsonval movement, calibrated to indicate sine-wave RMS amplitude, will only be accurate when measuring pure sine waves. If the waveform of the voltage or current being measured is anything but a pure sine wave, the indication given by the meter will not be the true RMS value of the waveform, because the degree of needle deflection in an analog D’Arsonval meter movement is proportional to the average value of the waveform, not the RMS. RMS meter calibration is obtained by “skewing” the span of the meter so that it displays a small multiple of the average value, which will be equal to be the RMS value for a particular waveshape and a particular waveshape only.
Since the sine-wave shape is most common in electrical measurements, it is the waveshape assumed for analog meter calibration, and the small multiple used in the calibration of the meter is 1.1107 (the form factor: 0.707/0.636: the ratio of RMS divided by average for a sinusoidal waveform). Any waveshape other than a pure sine wave will have a different ratio of RMS and average values, and thus a meter calibrated for sine-wave voltage or current will not indicate true RMS when reading a non-sinusoidal wave. Bear in mind that this limitation applies only to simple, analog AC meters not employing “True-RMS” technology.
- The amplitude of an AC waveform is its height as depicted on a graph over time. An amplitude measurement can take the form of peak, peak-to-peak, average, or RMS quantity.
- Peak amplitude is the height of an AC waveform as measured from the zero mark to the highest positive or lowest negative point on a graph. Also known as the crest amplitude of a wave.
- Peak-to-peak amplitude is the total height of an AC waveform as measured from maximum positive to maximum negative peaks on a graph. Often abbreviated as “P-P”.
- Average amplitude is the mathematical “mean” of all a waveform’s points over the period of one cycle. Technically, the average amplitude of any waveform with equal-area portions above and below the “zero” line on a graph is zero. However, as a practical measure of amplitude, a waveform’s average value is often calculated as the mathematical mean of all the points’ absolute values (taking all the negative values and considering them as positive). For a sine wave, the average value so calculated is approximately 0.637 of its peak value.
- “RMS” stands for Root Mean Square, and is a way of expressing an AC quantity of voltage or current in terms functionally equivalent to DC. For example, 10 volts AC RMS is the amount of voltage that would produce the same amount of heat dissipation across a resistor of given value as a 10 volt DC power supply. Also known as the “equivalent” or “DC equivalent” value of an AC voltage or current. For a sine wave, the RMS value is approximately 0.707 of its peak value.
- The crest factor of an AC waveform is the ratio of its peak (crest) to its RMS value.
- The form factor of an AC waveform is the ratio of its RMS value to its average value.
- Analog, electromechanical meter movements respond proportionally to the average value of an AC voltage or current. When RMS indication is desired, the meter’s calibration must be “skewed” accordingly. This means that the accuracy of an electromechanical meter’s RMS indication is dependent on the purity of the waveform: whether it is the exact same waveshape as the waveform used in calibrating.
4.3 Single-phase Power Systems
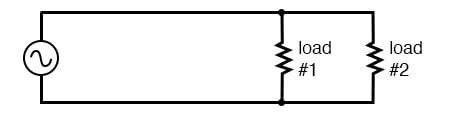
Depicted above, is a very simple AC circuit. If the load resistor’s power dissipation were substantial, we might call this a “power circuit” or “power system” instead of regarding it as just a regular circuit. The distinction between a “power circuit” and a “regular circuit” may seem arbitrary, but the practical concerns are definitely not.
Practical Circuit Analysis
One such concern is the size and cost of wiring necessary to deliver power from the AC source to the load. Normally, we do not give much thought to this type of concern if we’re merely analyzing a circuit for the sake of learning about the laws of electricity. However, in the real world, it can be a major concern. If we give the source in the above circuit a voltage value and also give power dissipation values to the two load resistors, we can determine the wiring needs for this particular circuit:

As a practical matter, the wiring for the 20 kW loads at 120 Vac is rather substantial (167 A).
[latex]I=\frac{P}{E}[/latex]
[latex]I=\frac{10kW}{120V}[/latex]
[latex]I=83.33A \text{(for each load resistor)}[/latex]
[latex]I_{total}= I_\text{load#1} + I_\text{load#2}[/latex]
[latex]P_{total}= (10kW) +(10kW)[/latex]
[latex]I_{total}= (83.33 A) +(83.33 A)[/latex]
[latex]P_{total}= (20kW)[/latex]
[latex]\pmb{I_{total}= 166.67 A}[/latex]
From the example above, 83.33 amps for each load resistor in the figure above adds up to 166.66 amps total circuit current. This is no small amount of current and would necessitate copper wire conductors of at least 1/0 gage. Such wire is well over 1/4 inch (6 mm) in diameter, weighing over 300 pounds per thousand feet. Bear in mind that copper is not cheap either! It would be in our best interest to find ways to minimize such costs if we were designing a power system with long conductor lengths.
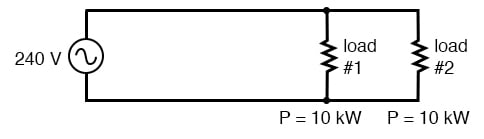
One way to do this would be to increase the voltage of the power source and use loads built to dissipate 10 kW each at this higher voltage. The loads, of course, would have to have greater resistance values to dissipate the same power as before (10 kW each) at a greater voltage than before. The advantage would be less current required, permitting the use of smaller, lighter, and cheaper wire:
[latex]I=\frac{P}{E}[/latex]
[latex]I=\frac{10kW}{240V}[/latex]
[latex]I=41.67 A \text{ (for each load resistor)}[/latex]
[latex]I_{total}= I_\text{load#1} + I_\text{load#2}[/latex]
[latex]P_{total}= (10kW) +(10kW)[/latex]
[latex]I_{total}= (41.67 A) +(41.67 A)[/latex]
[latex]P_{total}= (20kW)[/latex]
[latex]\pmb{I_{total}= 83.33 A}[/latex]
Now our total circuit current is 83.33 amps, half of what it was before. We can now use number 4 gauge wire, which weighs less than half of what 1/0 gauge wire does per unit length. This is a considerable reduction in system cost with no degradation in performance. This is why power distribution system designers elect to transmit electric power using very high voltages (many thousands of volts): to capitalize on the savings realized by the use of smaller, lighter, cheaper wire.
Dangers of Increasing the Source Voltage
However, this solution is not without disadvantages. Another practical concern with power circuits is the danger of electric shock from high voltages. Again, this is not usually the sort of thing we concentrate on while learning about the laws of electricity, but it is a very valid concern in the real world, especially when large amounts of power are being dealt with. The gain in efficiency realized by stepping up the circuit voltage presents us with an increased danger of electric shock. Power distribution companies tackle this problem by stringing their power lines along high poles or towers and insulating the lines from the supporting structures with large, porcelain insulators.
At the point of use (the electric power customer), there is still the issue of what voltage to use for powering loads. High voltage gives greater system efficiency by means of reduced conductor current, but it might not always be practical to keep power wiring out of reach at the point of use the way it can be elevated out of reach in distribution systems. This tradeoff between efficiency and danger is one that European power system designers have decided to risk, all their households and appliances operating at a nominal voltage of 240 volts instead of 120 volts as it is in North America. That is why tourists from America visiting Europe must carry small step-down transformers for their portable appliances, to step the 240 VAC (volts AC) power down to a more suitable 120 VAC.
Solutions for Voltage Delivery to Consumers
Step-down Transformers at End-point of Power use
Is there any way to realize the advantages of both increased efficiency and reduced safety hazard at the same time? One solution would be to install step-down transformers at the end-point of power use, just as the American tourist must do while in Europe. However, this would be expensive and inconvenient for anything but very small loads (where the transformers can be built cheaply) or very large loads (where the expense of thick copper wires would exceed the expense of a transformer).
Two Lower voltage Loads in Series
An alternative solution would be to use a higher voltage supply to provide power to two lower voltage loads in series. This approach combines the efficiency of a high-voltage system with the safety of a low-voltage system:

Notice the polarity markings (+ and -) for each voltage shown, as well as the unidirectional arrows for current. For the most part, I’ve avoided labeling “polarities” in the AC circuits we’ve been analyzing, even though the notation is valid to provide a frame of reference for phase. In later sections of this chapter, phase relationships will become very important, so I’m introducing this notation early on in the chapter for your familiarity.
The current through each load is the same as it was in the simple 120-volt circuit, but the currents are not additive because the loads are in series rather than parallel. The voltage across each load is only 120 volts, not 240, so the safety factor is better. Mind you, we still have a full 240 volts across the power system wires, but each load is operating at a reduced voltage. If anyone is going to get shocked, the odds are that it will be from coming into contact with the conductors of a particular load rather than from contact across the main wires of a power system.
Modifications to Two Load Series Design
There’s only one disadvantage to this design: the consequences of one load failing open, or being turned off (assuming each load has a series on/off switch to interrupt current) are not good. Being a series circuit, if either load were to open, the current would stop in the other load as well. For this reason, we need to modify the design a bit:

[latex]E_{total } = {(120V 0^\circ )}+{(120V 0^\circ)}[/latex] [latex]= 240 V0^\circ[/latex] [latex]I_1=\frac{P_1}{E_1}[/latex] [latex]=\frac{10kW}{120V}[/latex] [latex]I_1=83.33 A[/latex] [latex]I_2=\frac{P_2}{E_2}[/latex] [latex]=\frac{10kW}{120V}[/latex] [latex]I_2=83.33 A[/latex] [latex]P_{total}= (10kW) +(10kW)[/latex] [latex]= (20kW)[/latex]
Split-phase Power System
Instead of a single 240-volt power supply, we use two 120 volt supplies (in phase with each other!) in series to produce 240 volts, then run a third wire to the connection point between the loads to handle the eventuality of one load opening. This is called a split-phase power system. Three smaller wires are still cheaper than the two wires needed with the simple parallel design, so we’re still ahead on efficiency. The astute observer will note that the neutral wire only has to carry the difference of current between the two loads back to the source. In the above case, with perfectly “balanced” loads consuming equal amounts of power, the neutral wire carries zero current.
Notice how the neutral wire is connected to earth ground at the power supply end. This is a common feature in power systems containing “neutral” wires, since grounding the neutral wire ensures the least possible voltage at any given time between any “hot” wire and earth ground.
An essential component of a split-phase power system is the dual AC voltage source. Fortunately, designing and building one is not difficult. Since most AC systems receive their power from a step-down transformer anyway (stepping voltage down from high distribution levels to a user-level voltage like 120 or 240), that transformer can be built with a center-tapped secondary winding:

If the AC power comes directly from a generator (alternator), the coils can be similarly center-tapped for the same effect. The extra expense to include a center-tap connection in a transformer or alternator winding is minimal.
Here is where the (+) and (-) polarity markings really become important. This notation is often used to reference the phasings of multiple AC voltage sources, so it is clear whether they are aiding (“boosting”) each other or opposing (“bucking”) each other. If not for these polarity markings, phase relations between multiple AC sources might be very confusing. Note that the split-phase sources in the schematic (each one 120 volts ∠ 0°), with polarity marks (+) to (-) just like series-aiding batteries can alternatively be represented as such:

To mathematically calculate voltage between “hot” wires, we must subtract voltages, because their polarity marks show them to be opposed to each other:
Polar
[latex]\begin{align} & 120 \angle 0\text{°} \\ - & 120 \angle 180\text{°} \\ = & \pmb{120 \angle 0\text{°}}\end{align}[/latex]
Rectangular
[latex]\begin{align} & 120 + \text{j}0 \text{ V} \\ - & (-{120} + \text{j}0) \text{ V} \\ = & \pmb{240 + \text{j}0 \text{ V}}\end{align}[/latex]
If we mark the two sources’ common connection point (the neutral wire) with the same polarity mark (-), we must express their relative phase shifts as being 180° apart. Otherwise, we’d be denoting two voltage sources in direct opposition with each other, which would give 0 volts between the two “hot” conductors. Why am I taking the time to elaborate on polarity marks and phase angles? It will make more sense in the next section!
Power systems in American households and light industry are most often of the split-phase variety, providing so-called 120/240 VAC power. The term “split-phase” merely refers to the split-voltage supply in such a system. In a more general sense, this kind of AC power supply is called single phase because both voltage waveforms are in phase, or in step, with each other.
The term “single phase” is a counterpoint to another kind of power system called “polyphase” which we are about to investigate in detail. Apologies for the long introduction leading up to the title-topic of this chapter. The advantages of polyphase power systems are more obvious if one first has a good understanding of single-phase systems.
- Single phase power systems are defined by having an AC source with only one voltage waveform.
- A split-phase power system is one with multiple (in-phase) AC voltage sources connected in series, delivering power to loads at more than one voltage, with more than two wires. They are used primarily to achieve a balance between system efficiency (low conductor currents) and safety (low load voltages).
- Split-phase AC sources can be easily created by center-tapping the coil windings of transformers or alternators.
4.4 AC phase
AC phase
Things start to get complicated when we need to relate two or more AC voltages or currents that are out of step with each other. By “out of step,” I mean that the two waveforms are not synchronized: that their peaks and zero points do not match up at the same points in time. The graph in figure below illustrates an example of this.

The two waves shown above (A versus B) are of the same amplitude and frequency, but they are out of step with each other. In technical terms, this is called a phase shift. Earlier we saw how we could plot a “sine wave” by calculating the trigonometric sine function for angles ranging from 0 to 360 degrees, a full circle. The starting point of a sine wave was zero amplitude at zero degrees, progressing to full positive amplitude at 90 degrees, zero at 180 degrees, full negative at 270 degrees, and back to the starting point of zero at 360 degrees. We can use this angle scale along the horizontal axis of our waveform plot to express how far out of step one wave is with another:

The shift between these two waveforms is about 45 degrees, the “A” wave being ahead of the “B” wave. A sampling of different phase shifts is given in the following graphs to better illustrate this concept:
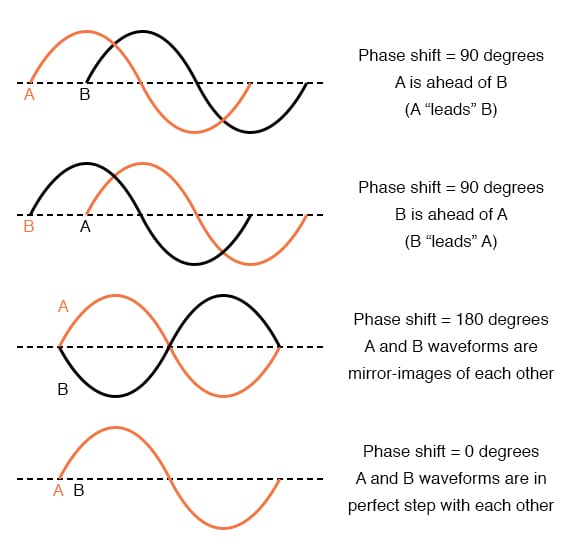
Because the waveforms in the above examples are at the same frequency, they will be out of step by the same angular amount at every point in time. For this reason, we can express phase shift for two or more waveforms of the same frequency as a constant quantity for the entire wave, and not just an expression of shift between any two particular points along the waves. That is, it is safe to say something like, “voltage ‘A’ is 45 degrees out of phase with voltage ‘B’.” Whichever waveform is ahead in its evolution is said to be leading and the one behind is said to be lagging. Phase shift, like voltage, is always a measurement relative between two things. There’s really no such thing as a waveform with an absolute phase measurement because there’s no known universal reference for phase. Typically in the analysis of AC circuits, the voltage waveform of the power supply is used as a reference for phase, that voltage stated as “xxx volts at 0 degrees.” Any other AC voltage or current in that circuit will have its phase shift expressed in terms relative to that source voltage. This is what makes AC circuit calculations more complicated than DC. When applying Ohm’s Law and Kirchhoff’s Laws, quantities of AC voltage and current must reflect phase shift as well as amplitude. Mathematical operations of addition, subtraction, multiplication, and division must operate on these quantities of phase shift as well as amplitude. Fortunately, there is a mathematical system of quantities called complex numbers ideally suited for this task of representing amplitude and phase. Because the subject of complex numbers is so essential to the understanding of AC circuits, the next chapter will be devoted to that subject alone.
- Phase shift is where two or more waveforms are out of step with each other.
- The amount of phase shift between two waves can be expressed in terms of degrees, as defined by the degree units on the horizontal axis of the waveform graph used in plotting the trigonometric sine function.
- A leading waveform is defined as one waveform that is ahead of another in its evolution. A lagging waveform is one that is behind another. Example:

- Calculations for AC circuit analysis must take into consideration both amplitude and phase shift of voltage and current waveforms to be completely accurate. This requires the use of a mathematical system called complex numbers.
4.5 Three-phase Power Systems
What is Split-Phase Power Systems?
Split-phase power systems achieve their high conductor efficiency and low safety risk by splitting up the total voltage into lesser parts and powering multiple loads at those lesser voltages while drawing currents at levels typical of a full-voltage system. This technique, by the way, works just as well for DC power systems as it does for single-phase AC systems. Such systems are usually referred to as three-wire systems rather than split-phase because “phase” is a concept restricted to AC.
But we know from our experience with vectors and complex numbers that AC voltages don’t always add up as we think they would if they are out of phase with each other. This principle, applied to power systems, can be put to use to make power systems with even greater conductor efficiencies and lower shock hazard than with split-phase.
Two 120° Out of Phase Voltage Sources
Suppose that we had two sources of AC voltage connected in series just like the split-phase system we saw before, except that each voltage source was 120° out of phase with the other: (Figure below)
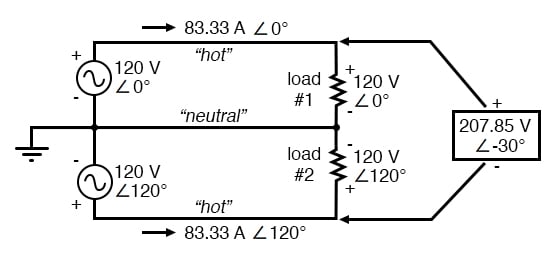
Since each voltage source is 120 volts, and each load resistor is connected directly in parallel with its respective source, the voltage across each load must be 120 volts as well. Given load currents of 83.33 amps, each load must still be dissipating 10 kilowatts of power. However, voltage between the two “hot” wires is not 240 volts (120 ∠ 0° – 120 ∠ 180°) because the phase difference between the two sources is not 180°. Instead, the voltage is:
[latex]E_{total} = (120 \text{ V } \angle \text{ 0°}) - (120 \text{ V } \angle \text{ 120°})[/latex]
[latex]\pmb{E_{total} = 207.85 \text{ V } \angle \text{ -30°}}[/latex]
Nominally, we say that the voltage between “hot” conductors is 208 volts (rounding up), and thus the power system voltage is designated as 120/208 V.
If we calculate the current through the “neutral” conductor, we find that it is not zero, even with balanced load resistances. Kirchhoff’s Current Law tells us that the currents entering and exiting the node between the two loads must be zero:

[latex]I_{\text{load#1}} + I_{\text{load#2}} + I_{\text{neutral}}=0A[/latex]
[latex]\begin{align} I_{\text{neutral}} = & -I_{\text{load#1}} - I_{\text{load#2}} \\ = & -(83.33 A \angle \text{ 0°}) - (83.33 A \angle \text{ 120°}) \\ = & \pmb{83.33 A \angle \text{ 240°}} \text{ or } \pmb{83.33 A \angle \text{-120°}} \end{align}[/latex]
So, we find that the “neutral” wire is carrying a full 83.33 amps, just like each “hot” wire.
Note that we are still conveying 20 kW of total power to the two loads, with each load’s “hot” wire carrying 83.33 amps as before. With the same amount of current through each “hot” wire, we must use the same gauge copper conductors, so we haven’t reduced system cost over the split-phase 120/240 system. However, we have realized a gain in safety, because the overall voltage between the two “hot” conductors is 32 volts lower than it was in the split-phase system (208 volts instead of 240 volts).
Three 120° Out of Phase Voltage Sources
The fact that the neutral wire is carrying 83.33 amps of current raises an interesting possibility: since its carrying current anyway, why not use that third wire as another “hot” conductor, powering another load resistor with a third 120 volt source having a phase angle of 240°? That way, we could transmit more power (another 10 kW) without having to add any more conductors. Let’s see how this might look:

Polyphase Circuit
This circuit we’ve been analyzing with three voltage sources is called a polyphase circuit. The prefix “poly” simply means “more than one,” as in “polytheism” (belief in more than one deity), “polygon” (a geometrical shape made of multiple line segments: for example, pentagon and hexagon), and “polyatomic” (a substance composed of multiple types of atoms). Since the voltage sources are all at different phase angles (in this case, three different phase angles), this is a “polyphase” circuit. More specifically, it is a three-phase circuit, the kind used predominantly in large power distribution systems.
Single-Phase System
Let’s survey the advantages of a three-phase power system over a single-phase system of equivalent load voltage and power capacity. A single-phase system with three loads connected directly in parallel would have a very high total current (83.33 times 3, or 250 amps.

This would necessitate 3/0 gage copper wire (very large!), at about 510 pounds per thousand feet, and with a considerable price tag attached. If the distance from source to load was 1000 feet, we would need over a half-ton of copper wire to do the job.
Split-phase System
On the other hand, we could build a split-phase system with two 15 kW, 120 volt loads.

Our current is half of what it was with the simple parallel circuit, which is a great improvement. We could get away with using number 2 gauge copper wire at a total mass of about 600 pounds, figuring about 200 pounds per thousand feet with three runs of 1000 feet each between source and loads. However, we also have to consider the increased safety hazard of having 240 volts present in the system, even though each load only receives 120 volts. Overall, there is greater potential for a dangerous electric shock to occur.
Three-Phase System
When we contrast these two examples against our three-phase system (Figure above), the advantages are quite clear. First, the conductor currents are quite a bit less (83.33 amps versus 125 or 250 amps), permitting the use of much thinner and lighter wire. We can use number 4 gauge wire at about 125 pounds per thousand feet, which will total 500 pounds (four runs of 1000 feet each) for our example circuit. This represents significant cost savings over the split-phase system, with the additional benefit that the maximum voltage in the system is lower (208 versus 240).
One question remains to be answered: how in the world do we get three AC voltage sources whose phase angles are exactly 120° apart? Obviously we can’t center-tap a transformer or alternator winding like we did in the split-phase system, since that can only give us voltage waveforms that are either in phase or 180° out of phase. Perhaps we could figure out some way to use capacitors and inductors to create phase shifts of 120°, but then those phase shifts would depend on the phase angles of our load impedances as well (substituting a capacitive or inductive load for a resistive load would change everything!).
The best way to get the phase shifts we’re looking for is to generate it at the source: construct the AC generator (alternator) providing the power in such a way that the rotating magnetic field passes by three sets of wire windings, each set spaced 120o apart around the circumference of the machine as in the figure below.

Together, the six “pole” windings of a three-phase alternator are connected to comprise three winding pairs, each pair producing AC voltage with a phase angle 120° shifted from either of the other two winding pairs. The interconnections between pairs of windings (as shown for the single-phase alternator: the jumper wire between windings 1a and 1b) have been omitted from the three-phase alternator drawing for simplicity.
In our example circuit, we showed the three voltage sources connected together in a “Y” configuration (sometimes called the “star” configuration), with one lead of each source tied to a common point (the node where we attached the “neutral” conductor). The common way to depict this connection scheme is to draw the windings in the shape of a “Y” like the figure below.

The “Y” configuration is not the only option open to us, but it is probably the easiest to understand at first. More to come on this subject later in the chapter.
- A single-phase power system is one where there is only one AC voltage source (one source voltage waveform).
- A split-phase power system is one where there are two voltage sources, 180° phase-shifted from each other, powering a two series-connected loads. The advantage of this is the ability to have lower conductor currents while maintaining low load voltages for safety reasons.
- A polyphase power system uses multiple voltage sources at different phase angles from each other (many “phases” of voltage waveforms at work). A polyphase power system can deliver more power at less voltage with smaller-gage conductors than single- or split-phase systems.
- The phase-shifted voltage sources necessary for a polyphase power system are created in alternators with multiple sets of wire windings. These winding sets are spaced around the circumference of the rotor’s rotation at the desired angle(s).
4.6 Phase Rotation
Three-Phase Alternator
Let’s take the three-phase alternator design laid out earlier and watch what happens as the magnet rotates.

The phase angle shift of 120° is a function of the actual rotational angle shift of the three pairs of windings. If the magnet is rotating clockwise, winding 3 will generate its peak instantaneous voltage exactly 120° (of alternator shaft rotation) after winding 2, which will hit its peak 120° after winding 1. The magnet passes by each pole pair at different positions in the rotational movement of the shaft. Where we decide to place the windings will dictate the amount of phase shift between the windings’ AC voltage waveforms. If we make winding 1 our “reference” voltage source for phase angle (0°), then winding 2 will have a phase angle of -120° (120° lagging, or 240° leading) and winding 3 an angle of -240° (or 120° leading).
Phase Sequence
This sequence of phase shifts has a definite order. For clockwise rotation of the shaft, the order is 1-2-3 (winding 1 peak first, them winding 2, then winding 3). This order keeps repeating itself as long as we continue to rotate the alternator’s shaft.

However, if we reverse the rotation of the alternator’s shaft (turn it counter-clockwise), the magnet will pass by the pole pairs in the opposite sequence. Instead of 1-2-3, we’ll have 3-2-1. Now, winding 2’s waveform will be leading 120° ahead of 1 instead of lagging, and 3 will be another 120° ahead of 2.

The order of voltage waveform sequences in a polyphase system is called phase rotation or phase sequence. If we’re using a polyphase voltage source to power resistive loads, phase rotation will make no difference at all. Whether 1-2-3 or 3-2-1, the voltage and current magnitudes will all be the same. There are some applications of three-phase power, as we will see shortly, that depend on having phase rotation being one way or the other.
Phase Sequence Detectors
Since voltmeters and ammeters would be useless in telling us what the phase rotation of an operating power system is, we need to have some other kind of instrument capable of doing the job.
One ingenious circuit design uses a capacitor to introduce a phase shift between voltage and current, which is then used to detect the sequence by way of comparison between the brightness of two indicator lamps in the figure below.

The two lamps are of equal filament resistance and wattage. The capacitor is sized to have approximately the same amount of reactance at system frequency as each lamp’s resistance. If the capacitor were to be replaced by a resistor of equal value to the lamps’ resistance, the two lamps would glow at equal brightness, the circuit is balanced. However, the capacitor introduces a phase shift between voltage and current in the third leg of the circuit equal to 90°. This phase shift, greater than 0° but less than 120°, skews the voltage and current values across the two lamps according to their phase shifts relative to phase 3.
Exchanging Hot Wires
There is a much easier way to reverse phase sequence than reversing alternator rotation: just exchange any two of the three “hot” wires going to a three-phase load.
This trick makes more sense if we take another look at a running phase sequence of a three-phase voltage source:
1-2-3 rotation: 1-2-3-1-2-3-1-2-3-1-2-3-1-2-3 . . .
3-2-1 rotation: 3-2-1-3-2-1-3-2-1-3-2-1-3-2-1 . . .
What is commonly designated as a “1-2-3” phase rotation could just as well be called “2-3-1” or “3-1-2,” going from left to right in the number string above? Likewise, the opposite rotation (3-2-1) could just as easily be called “2-1-3” or “1-3-2.”
Starting out with a phase rotation of 3-2-1, we can try all the possibilities for swapping any two of the wires at a time and see what happens to the resulting sequence in the figure below.

No matter which pair of “hot” wires out of the three we choose to swap, the phase rotation ends up being reversed (1-2-3 gets changed to 2-1-3, 1-3-2 or 3-2-1, all equivalent).
- Phase rotation, or phase sequence, is the order in which the voltage waveforms of a polyphase AC source reach their respective peaks. For a three-phase system, there are only two possible phase sequences: 1-2-3 and 3-2-1, corresponding to the two possible directions of alternator rotation.
- Phase rotation has no impact on resistive loads, but it will have an impact on unbalanced reactive loads, as shown in the operation of a phase rotation detector circuit.
- Phase rotation can be reversed by swapping any two of the three “hot” leads supplying three-phase power to a three-phase load.
4.7 Three-phase Y and Delta Configurations
Three-phase Wye(Y) Connection
Initially, we explored the idea of three-phase power systems by connecting three voltage sources together in what is commonly known as the “Y” (or “star”) configuration. This configuration of voltage sources is characterized by a common connection point joining one side of each source.
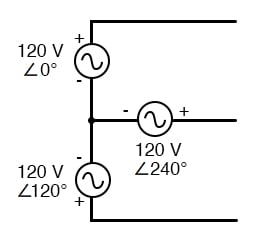
If we draw a circuit showing each voltage source to be a coil of wire (alternator or transformer winding) and do some slight rearranging, the “Y” configuration becomes more obvious in the figure below.

The three conductors leading away from the voltage sources (windings) toward a load are typically called lines, while the windings themselves are typically called phases. In a Y-connected system, there may or may not (Figure below) be a neutral wire attached at the junction point in the middle, although it certainly helps alleviate potential problems should one element of a three-phase load fail open, as discussed earlier.
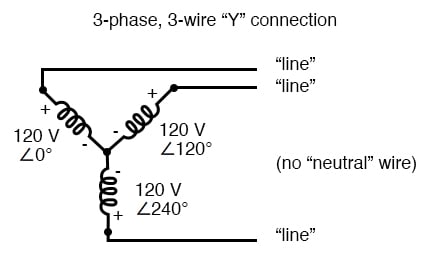
Voltage and Current Values in Three-Phase Systems
When we measure voltage and current in three-phase systems, we need to be specific as to where we’re measuring. Line voltage refers to the amount of voltage measured between any two line conductors in a balanced three-phase system. With the above circuit, the line voltage is roughly 208 volts. Phase voltage refers to the voltage measured across any one component (source winding or load impedance) in a balanced three-phase source or load. For the circuit shown above, the phase voltage is 120 volts. The terms line current and phase current follows the same logic: the former referring to the current through any one line conductor, and the latter to the current through any one component.
Y-connected sources and loads always have line voltages greater than phase voltages, and line currents equal to phase currents. If the Y-connected source or load is balanced, the line voltage will be equal to the phase voltage times the square root of 3:
For “Y” circuits:
[latex]\begin{align} \tag{4.1} \text{E}_{\text{line}} &= \sqrt{3} \text{ E}_{\text{phase}} \\ \text{I}_{\text{line}} &= \text{ I}_{\text{phase}} \end{align}[/latex]
However, the “Y” configuration is not the only valid one for connecting three-phase voltage source or load elements together.
Three-Phase Delta(Δ) Configuration
Another configuration is known as the “Delta,” for its geometric resemblance to the Greek letter of the same name (Δ). Take close notice of the polarity for each winding in the figure below.
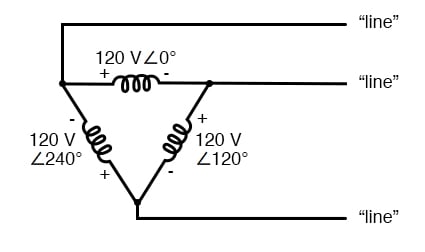
At first glance, it seems as though three voltage sources like this would create a short-circuit, electrons flowing around the triangle with nothing but the internal impedance of the windings to hold them back. Due to the phase angles of these three voltage sources, however, this is not the case.
Kirchhoff’s Voltage Law in Delta Connections
One quick check of this is to use Kirchhoff’s Voltage Law to see if the three voltages around the loop add up to zero. If they do, then there will be no voltage available to push current around and around that loop, and consequently, there will be no circulating current. Starting with the top winding and progressing counter-clockwise, our KVL expression looks something like this:
[latex](120 \text{ V} \angle \text{ 0°}) +(120\text{ V} \angle \text{ 240°}) + (120\text{ V} \angle \text{ 120°})[/latex]
Does it all equal zero?
Yes!
Indeed, if we add these three vector quantities together, they do add up to zero. Another way to verify the fact that these three voltage sources can be connected together in a loop without resulting in circulating currents is to open up the loop at one junction point and calculate the voltage across the break:

Starting with the right winding (120 V ∠ 120°) and progressing counter-clockwise, our KVL equation looks like this:
[latex](120\text{ V} \angle \text{120°}) +(120\text{ V} \angle \text{0°}) + (120\text{ V} \angle \text{ 240°}) + \text{E}_{\text{break}} = 0[/latex]
[latex]0 + \text{E}_{\text{break}} = 0[/latex]
[latex]\text{E}_{\text{break}} = 0[/latex]
Sure enough, there will be zero voltage across the break, telling us that no current will circulate within the triangular loop of windings when that connection is made complete.
Having established that a Δ-connected three-phase voltage source will not burn itself to a crisp due to circulating currents, we turn to its practical use as a source of power in three-phase circuits. Because each pair of line conductors is connected directly across a single winding in a Δ circuit, the line voltage will be equal to the phase voltage. Conversely, because each line conductor attaches at a node between two windings, the line current will be the vector sum of the two joining phase currents. Not surprisingly, the resulting equations for a Δ configuration are as follows:
For Δ (“Delta”) circuits:
[latex]\begin{align} \tag{4.2} \text{E}_{\text{line}} &= \text{E}_{\text{phase}} \\ \text{I}_{\text{line}} &= \sqrt{3} \text{ I}_{\text{phase}} \end{align}[/latex]
Delta Connection Example Circuit Analysis
Let’s see how this works in an example circuit: (Figure below)

With each load resistance receiving 120 volts from its respective phase winding at the source, the current in each phase of this circuit will be 83.33 amps:
[latex]I \:=\frac{P}{E}[/latex]
[latex]I \:=\frac{10 kW}{120 V}[/latex]
[latex]\pmb{I = 83.33A} \text{ (for each load resistor and source winding)}[/latex]
[latex]\text{I}_{\text{line}} = √3 \text{ I}_{\text{phase}}[/latex]
[latex]\text{I}_{\text{line}} = √3 (83.33 A)[/latex]
[latex]\pmb{\text{I}_{\text{line}} = 144.34 A}[/latex]
Advantages of the Delta Three-Phase System
So each line current in this three-phase power system is equal to 144.34 amps, which is substantially more than the line currents in the Y-connected system we looked at earlier. One might wonder if we’ve lost all the advantages of three-phase power here, given the fact that we have such greater conductor currents, necessitating thicker, more costly wire. The answer is no. Although this circuit would require three number 1 gauge copper conductors (at 1000 feet of distance between source and load this equates to a little over 750 pounds of copper for the whole system), it is still less than the 1000+ pounds of copper required for a single-phase system delivering the same power (30 kW) at the same voltage (120 volts conductor-to-conductor).
One distinct advantage of a Δ-connected system is its lack of a neutral wire. With a Y-connected system, a neutral wire was needed in case one of the phase loads were to fail open (or be turned off), in order to keep the phase voltages at the load from changing. This is not necessary (or even possible!) in a Δ-connected circuit. With each load phase element directly connected across a respective source phase winding, the phase voltage will be constant regardless of open failures in the load elements.
Perhaps the greatest advantage of the Δ-connected source is its fault tolerance. It is possible for one of the windings in a Δ-connected three-phase source to fail open (Figure below) without affecting load voltage or current!

The only consequence of a source winding failing open for a Δ-connected source is increased phase current in the remaining windings. Compare this fault tolerance with a Y-connected system suffering an open source winding in the figure below.

With a Δ-connected load, two of the resistances suffer reduced voltage while one remains at the original line voltage, 208. A Y-connected load suffers an even worse fate (Figure below) with the same winding failure in a Y-connected source.

In this case, two load resistances suffer reduced voltage while the third loses supply voltage completely! For this reason, Δ-connected sources are preferred for reliability. However, if dual voltages are needed (e.g. 120/208) or preferred for lower line currents, Y-connected systems are the configuration of choice.
- The conductors connected to the three points of a three-phase source or load are called lines.
- The three components comprising a three-phase source or load are called phases.
- Line voltage is the voltage measured between any two lines in a three-phase circuit.
- Phase voltage is the voltage measured across a single component in a three-phase source or load.
- Line current is the current through any one line between a three-phase source and load.
- Phase current is the current through any one component comprising a three-phase source or load.
- In balanced “Y” circuits, the line voltage is equal to phase voltage times the square root of 3, while the line current is equal to phase current.
- For “Y” circuits:
[latex]\text{E}_{\text{line}} = \sqrt{3} \text{ E}_{\text{phase}}[/latex]
[latex]\text{I}_{\text{line}}= \text{ I}_{\text{phase}}[/latex]
- In balanced Δ circuits, the line voltage is equal to phase voltage, while the line current is equal to phase current times the square root of 3.
- For Δ (“Delta”) circuits:
[latex]\text{E}_{\text{line}} = \text{ E}_{\text{phase}}[/latex]
[latex]\text{I}_{\text{line}}= \sqrt{3} \text{ I}_{\text{phase}}[/latex]
- Δ-connected three-phase voltage sources give greater reliability in the event of winding failure than Y-connected sources. However, Y-connected sources can deliver the same amount of power with less line current than Δ-connected sources.
