APPENDIX B: Complex Number Review
Introduction to Complex Numbers
If I needed to describe the distance between two cities, I could provide an answer consisting of a single number in miles, kilometers, or some other unit of linear measurement. However, if I were to describe how to travel from one city to another, I would have to provide more information than just the distance between those two cities; I would also have to provide information about the direction to travel, as well.
The kind of information that expresses a single dimension, such as linear distance, is called a scalar quantity in mathematics. Scalar numbers are the kind of numbers you’ve used in most all of your mathematical applications so far. The voltage produced by a battery, for example, is a scalar quantity. So is the resistance of a piece of wire (ohms), or the current through it (amps).
However, when we begin to analyze AC circuits, we find that quantity of voltage, current, and even resistance (called impedance in AC) are not the familiar one-dimensional quantities we’re used to measuring in DC circuits. Rather, these quantities, because they’re dynamic (alternating in direction and amplitude), possess other dimensions that must be taken into account. Frequency and phase shift are two of these dimensions that come into play. Even with relatively simple AC circuits, where we’re only dealing with a single frequency, we still have the dimension of phase shift to contend with in addition to the amplitude.
In order to successfully analyze AC circuits, we need to work with mathematical objects and techniques capable of representing these multi-dimensional quantities. Here is where we need to abandon scalar numbers for something better suited: complex numbers. Just like the example of giving directions from one city to another, AC quantities in a single-frequency circuit have both amplitude (analogy: distance) and phase shift (analogy: direction). A complex number is a single mathematical quantity able to express these two dimensions of amplitude and phase shift at once.
Graphical Representation of Complex Numbers
Complex numbers are easier to grasp when they’re represented graphically. If I draw a line with a certain length (magnitude) and angle (direction), I have a graphic representation of a complex number which is commonly known in physics as a vector: (Figure below)

As distances and directions on a map, there must be some common frame of reference for angle figures to have any meaning. In this case, directly right is considered to be 0o, and angles are counted in a positive direction going counter-clockwise: (Figure below)

The idea of representing a number in graphical form is nothing new. We all learned this in grade school with the “number line:” (Figure below)

We even learned how addition and subtraction works by seeing how lengths (magnitudes) stacked up to give a final answer: (Figure below)

Later, we learned that there were ways to designate the values between the whole numbers marked on the line. These were fractional or decimal quantities: (Figure below)

These fields of numbers (whole, integer, rational, irrational, real, etc.) learned in grade school share a common trait: they’re all one-dimensional. The straightness of the number line illustrates this graphically. You can move up or down the number line, but all “motion” along that line is restricted to a single axis (horizontal). One-dimensional, scalar numbers are perfectly adequate for counting beads, representing weight, or measuring DC battery voltage, but they fall short of being able to represent something more complex like the distance and direction between two cities, or the amplitude and phase of an AC waveform. To represent these kinds of quantities, we need multidimensional representations. In other words, we need a number line that can point in different directions, and that’s exactly what a vector is.
- A scalar number is the type of mathematical object that people are used to using in everyday life: a one-dimensional quantity like temperature, length, weight, etc.
- A complex number is a mathematical quantity representing two dimensions of magnitude and direction.
- A vector is a graphical representation of a complex number. It looks like an arrow, with a starting point, a tip, a definite length, and a definite direction. Sometimes the word phasor is used in electrical applications where the angle of the vector represents the phase shift between waveforms.
Vectors and AC Waveforms
OK, so how exactly can we represent AC quantities of voltage or current in the form of a vector? The length of the vector represents the magnitude (or amplitude) of the waveform, like this: (Figure below)

The greater the amplitude of the waveform, the greater the length of its corresponding vector. The angle of the vector, however, represents the phase shift in degrees between the waveform in question and another waveform acting as a “reference” in time. Usually, when the phase of a waveform in a circuit is expressed, it is referenced to the power supply voltage waveform (arbitrarily stated to be “at” 0°). Remember that phase is always a relative measurement between two waveforms rather than an absolute property. (Figure below)


The greater the phase shift in degrees between two waveforms, the greater the angle difference between the corresponding vectors. Being a relative measurement, as the voltage, phase shift (vector angle) only has meaning in reference to some standard waveform. Generally, this “reference” waveform is the main AC power supply voltage in the circuit. If there is more than one AC voltage source, then one of those sources is arbitrarily chosen to be the phase reference for all other measurements in the circuit.
This concept of a reference point is not unlike that of the “ground” point in a circuit for the benefit of the voltage reference. With a clearly defined point in the circuit declared to be “ground,” it becomes possible to talk about voltage “on” or “at” single points in a circuit, being understood that those voltages (always relative between two points) are referenced to “ground.” Correspondingly, with a clearly defined point of reference for phase, it becomes possible to speak of voltages and currents in an AC circuit having definite phase angles. For example, if the current in an AC circuit is described as “24.3 milliamps at -64 degrees,” it means that the current waveform has an amplitude of 24.3 mA, and it lags 64° behind the reference waveform, usually assumed to be the main source voltage waveform.
Simple Vector Addition
Remember that vectors are mathematical objects just like numbers on a number line: they can be added, subtracted, multiplied, and divided. Addition is perhaps the easiest vector operation to visualize, so we’ll begin with that. If vectors with common angles are added, their magnitudes (lengths) add up just like regular scalar quantities: (Figure below)

Similarly, if AC voltage sources with the same phase angle are connected together in series, their voltages add just as you might expect with DC batteries: (Figure below)
Please note the (+) and (-) polarity marks next to the leads of the two AC sources. Even though we know AC doesn’t have “polarity” in the same sense that DC does, these marks are essential to know how to reference the given phase angles of the voltages. This will become more apparent in the next example.
If vectors directly opposing each other (180° out of phase) are added together, their magnitudes (lengths) subtract just like positive and negative scalar quantities subtract when added: (Figure below)

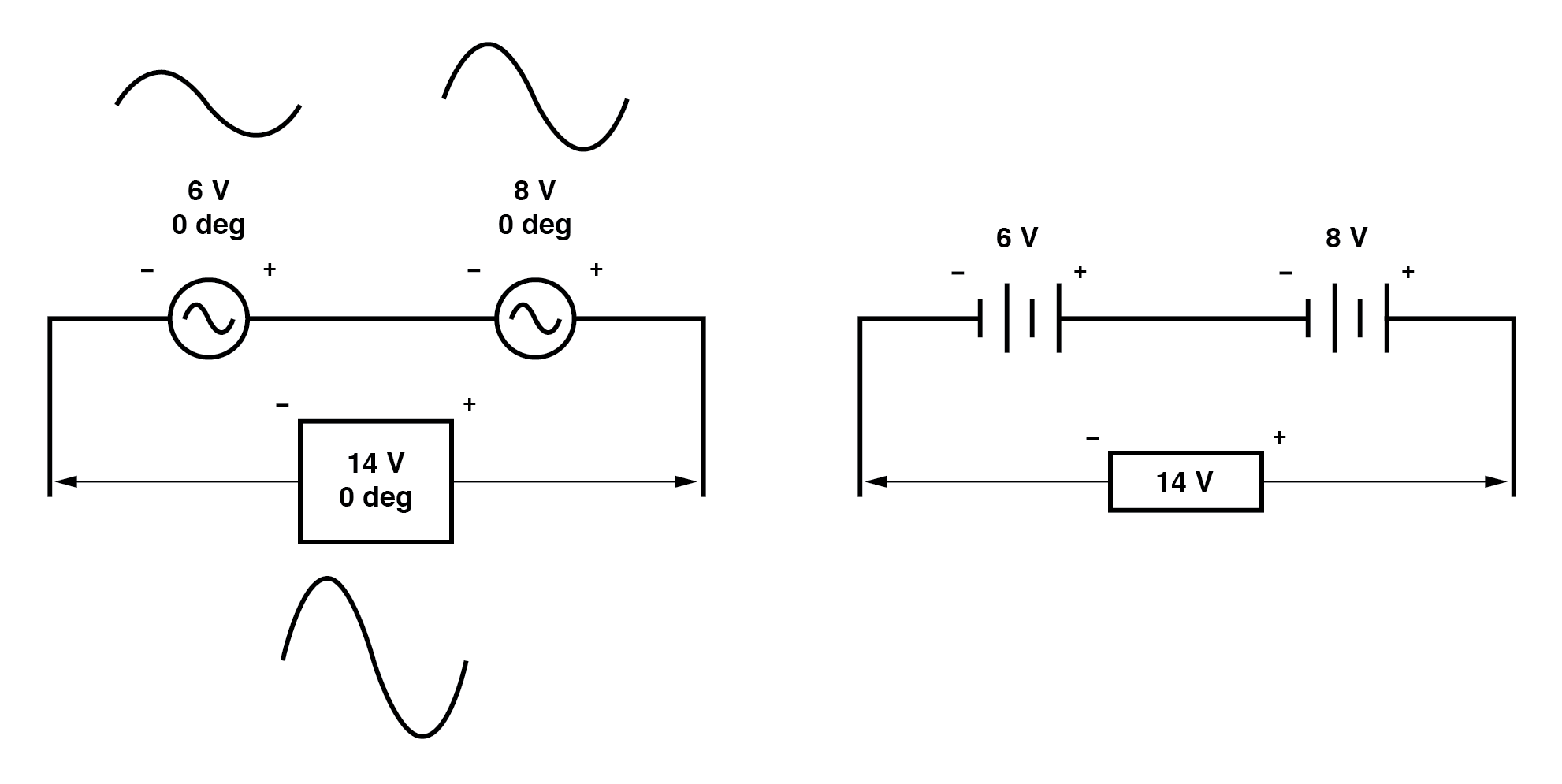
Similarly, if opposing AC voltage sources are connected in series, their voltages subtract as you might expect with DC batteries connected in an opposing fashion: (Figure below)

Determining whether or not these voltage sources are opposing each other requires an examination of their polarity markings and their phase angles. Notice how the polarity markings in the above diagram seem to indicate additive voltages (from left to right, we see – and + on the 6 volt source, – and + on the 8 volt source). Even though these polarity markings would normally indicate an additive effect in a DC circuit (the two voltages working together to produce a greater total voltage), in this AC circuit they’re actually pushing in opposite directions because one of those voltages has a phase angle of 0° and the other a phase angle of 180°. The result, of course, is a total voltage of 2 volts.
We could have just as well shown the opposing voltages subtracting in series like this: (Figure below)

Note how the polarities appear to be opposed to each other now, due to the reversal of wire connections on the 8 volt source. Since both sources are described as having equal phase angles (0°), they truly are opposed to one another, and the overall effect is the same as the former scenario with “additive” polarities and differing phase angles: a total voltage of only 2 volts. (Figure below)

Just as there are two ways to express the phase of the sources, there are two ways to express the resultant their sum.
The resultant voltage can be expressed in two different ways: 2 volts at 180° with the (-) symbol on the left and the (+) symbol on the right, or 2 volts at 0° with the (+) symbol on the left and the (-) symbol on the right. A reversal of wires from an AC voltage source is the same as phase-shifting that source by 180°. (Figure below)

Example of equivalent voltage sources.
Complex Vector Addition
If vectors with uncommon angles are added, their magnitudes (lengths) add up quite differently than that of scalar magnitudes: (Figure below)

Vector magnitudes do not directly add for unequal angles.
If two AC voltages—90° out of phase—are added together by being connected in series, their voltage magnitudes do not directly add or subtract as with scalar voltages in DC. Instead, these voltage quantities are complex quantities, and just like the above vectors, which add up in a trigonometric fashion, a 6-volt source at 0° added to an 8-volt source at 90° results in 10 volts at a phase angle of 53.13°: (Figure below)

The 6V and 8V sources add to 10V with the help of trigonometry.
Compared to DC circuit analysis, this is very strange indeed. Note that it is possible to obtain voltmeter indications of 6 and 8 volts, respectively, across the two AC voltage sources, yet only read 10 volts for a total voltage!
There is no suitable DC analogy for what we’re seeing here with two AC voltages slightly out of phase. DC voltages can only directly aid or directly oppose, with nothing in between. With AC, two voltages can be aiding or opposing one another to any degree between fully-aiding and fully-opposing, inclusive. Without the use of vector (complex number) notation to describe AC quantities, it would be very difficult to perform mathematical calculations for AC circuit analysis.
In the next section, we’ll learn how to represent vector quantities in symbolic rather than graphical form. Vector and triangle diagrams suffice to illustrate the general concept, but more precise methods of symbolism must be used if any serious calculations are to be performed on these quantities.
- DC voltages can only either directly aid or directly oppose each other when connected in series. AC voltages may aid or oppose to any degree depending on the phase shift between them.
Polar Form and Rectangular Form Notation for Complex Numbers
In order to work with complex numbers without drawing vectors, we first need some kind of standard mathematical notation. There are two basic forms of complex number notation: polar and rectangular.
Polar Form of a Complex Number
The polar form is where a complex number is denoted by the length (otherwise known as the magnitude, absolute value, or modulus) and the angle of its vector (usually denoted by an angle symbol that looks like this: ∠).
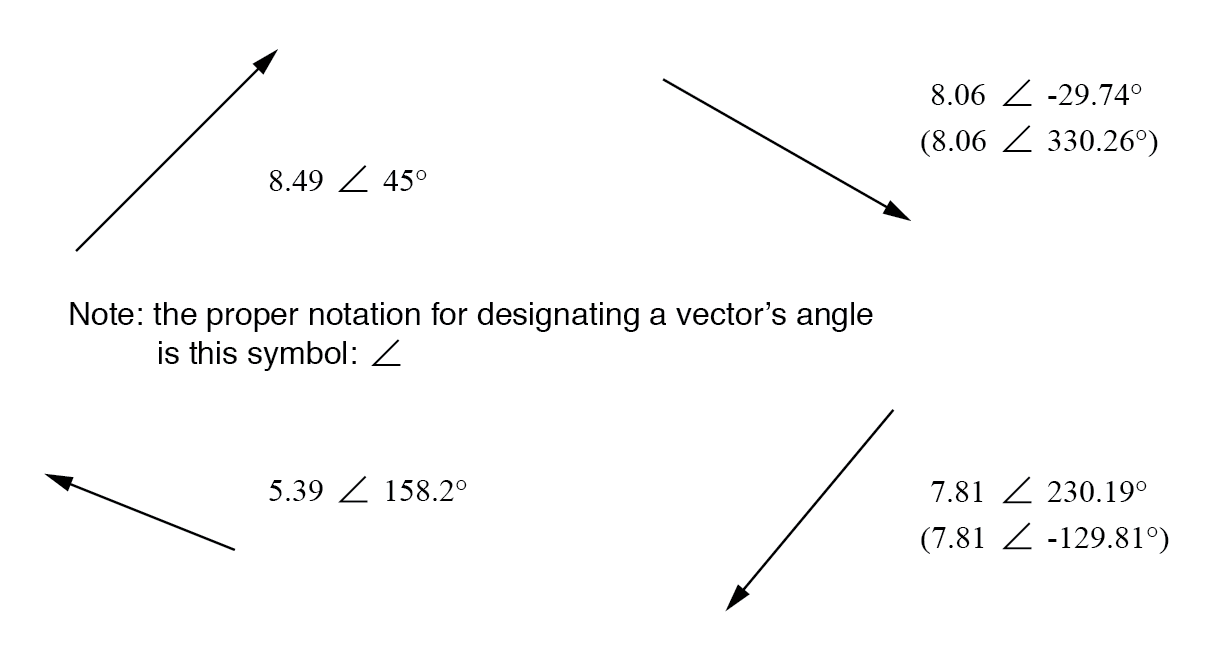
To use the map analogy, the polar notation for the vector from New York City to San Diego would be something like “2400 miles, southwest.” Here are two examples of vectors and their polar notations:
Vectors with polar notations.
Standard orientation for vector angles in AC circuit calculations defines 0° as being to the right (horizontal), making 90° straight up, 180° to the left, and 270° straight down. Please note that vectors angled “down” can have angles represented in polar form as positive numbers in excess of 180, or negative numbers less than 180. For example, a vector angled ∠ 270° (straight down) can also be said to have an angle of -90°. (Figure below) The above vector on the right (7.81 ∠ 230.19°) can also be denoted as 7.81 ∠ -129.81°.

The vector compass.
Rectangular Form of a Complex Number
Rectangular form, on the other hand, is where a complex number is denoted by its respective horizontal and vertical components. In essence, the angled vector is taken to be the hypotenuse of a right triangle, described by the lengths of the adjacent and opposite sides. Rather than describing a vector’s length and direction by denoting magnitude and angle, it is described in terms of “how far left/right” and “how far up/down.”
These two-dimensional figures (horizontal and vertical) are symbolized by two numerical figures. In order to distinguish the horizontal and vertical dimensions from each other, the vertical is prefixed with a lower-case “i” (in pure mathematics) or “j” (in electronics). These lower-case letters do not represent a physical variable (such as instantaneous current, also symbolized by a lower-case letter “i”), but rather are mathematical operators used to distinguish the vector’s vertical component from its horizontal component. As a complete complex number, the horizontal and vertical quantities are written as a sum: (Figure below)

In “rectangular” form the vector’s length and direction are denoted in terms of its horizontal and vertical span, the first number representing the horizontal (“real”) and the second number (with the “j” prefix) representing the vertical (“imaginary”) dimensions.
The horizontal component is referred to as the real component since that dimension is compatible with normal, scalar (“real”) numbers. The vertical component is referred to as the imaginary component since that dimension lies in a different direction, totally alien to the scale of the real numbers. (Figure below)

Vector compass showing real and imaginary axes.
The “real” axis of the graph corresponds to the familiar number line we saw earlier: the one with both positive and negative values on it. The “imaginary” axis of the graph corresponds to another number line situated at 90° to the “real” one. Vectors being two-dimensional things, we must have a two-dimensional “map” upon which to express them, thus the two number lines perpendicular to each other: (Figure below)

Vector compass with real and imaginary (“j”) number lines.
Converting from Polar Form to Rectangular Form
Either method of notation is valid for complex numbers. The primary reason for having two methods of notation is for ease of longhand calculation, rectangular form lending itself to addition and subtraction, and polar form lending itself to multiplication and division. Conversion between the two notational forms involves simple trigonometry. To convert from polar to rectangular, find the real component by multiplying the polar magnitude by the cosine of the angle, and the imaginary component by multiplying the polar magnitude by the sine of the angle. This may be understood more readily by drawing the quantities as sides of a right triangle, the hypotenuse of the triangle representing the vector itself (its length and angle with respect to the horizontal constituting the polar form), the horizontal and vertical sides representing the “real” and “imaginary” rectangular components, respectively: (Figure below)

Magnitude vector in terms of real (4) and imaginary (j3) components.

Converting from Rectangular Form to Polar Form
To convert from rectangular to polar, find the polar magnitude through the use of the Pythagorean Theorem (the polar magnitude is the hypotenuse of a right triangle, and the real and imaginary components are the adjacent and opposite sides, respectively), and the angle by taking the arctangent of the imaginary component divided by the real component:

- Polar notation denotes a complex number in terms of its vector’s length and angular direction from the starting point. Example: fly 45 miles ∠ 203° (West by Southwest).
- Rectangular notation denotes a complex number in terms of its horizontal and vertical dimensions. Example: drive 41 miles West, then turn and drive 18 miles South.
- In rectangular notation, the first quantity is the “real” component (horizontal dimension of the vector) and the second quantity is the “imaginary” component (vertical dimension of the vector). The imaginary component is preceded by a lower-case “j,” sometimes called the j operator.
- Both polar and rectangular forms of notation for a complex number can be related graphically in the form of a right triangle, with the hypotenuse representing the vector itself (polar form: hypotenuse length = magnitude; angle with respect to horizontal side = angle), the horizontal side representing the rectangular “real” component, and the vertical side representing the rectangular “imaginary” component.
Complex Number Arithmetic
Since complex numbers are legitimate mathematical entities, just like scalar numbers, they can be added, subtracted, multiplied, divided, squared, inverted, and such, just like any other kind of number. Some scientific calculators are programmed to directly perform these operations on two or more complex numbers, but these operations can also be done “by hand.” This section will show you how the basic operations are performed. It is highly recommended that you equip yourself with a scientific calculator capable of performing arithmetic functions easily on complex numbers. It will make your study of AC circuit much more pleasant than if you’re forced to do all calculations the longer way.
Addition and Subtraction of Complex Numbers in Rectangular Form
Addition and subtraction with complex numbers in rectangular form is easy. For addition, simply add up the real components of the complex numbers to determine the real component of the sum, and add up the imaginary components of the complex numbers to determine the imaginary component of the sum:

When subtracting complex numbers in rectangular form, simply subtract the real component of the second complex number from the real component of the first to arrive at the real component of the difference, and subtract the imaginary component of the second complex number from the imaginary component of the first to arrive the imaginary component of the difference:

Multiplication and Division of Complex Numbers in Polar Form
For longhand multiplication and division, polar is the favored notation to work with. When multiplying complex numbers in polar form, simply multiply the polar magnitudes of the complex numbers to determine the polar magnitude of the product, and add the angles of the complex numbers to determine the angle of the product:

Division of polar-form complex numbers is also easy: simply divide the polar magnitude of the first complex number by the polar magnitude of the second complex number to arrive at the polar magnitude of the quotient, and subtract the angle of the second complex number from the angle of the first complex number to arrive at the angle of the quotient:

To obtain the reciprocal, or “invert” (1/x), a complex number, simply divide the number (in polar form) into a scalar value of 1, which is nothing more than a complex number with no imaginary component (angle = 0):

These are the basic operations you will need to know in order to manipulate complex numbers in the analysis of AC circuits. Operations with complex numbers are by no means limited just to addition, subtraction, multiplication, division, and inversion, however. Virtually any arithmetic operation that can be done with scalar numbers can be done with complex numbers, including powers, roots, solving simultaneous equations with complex coefficients, and even trigonometric functions (although this involves a whole new perspective in trigonometry called hyperbolic functions which is well beyond the scope of this discussion). Be sure that you’re familiar with the basic arithmetic operations of addition, subtraction, multiplication, division, and inversion, and you’ll have little trouble with AC circuit analysis.
- To add complex numbers in rectangular form, add the real components and add the imaginary components. Subtraction is similar.
- To multiply complex numbers in polar form, multiply the magnitudes and add the angles. To divide, divide the magnitudes and subtract one angle from the other.
