Chapter 11: Multiple Trait Selection
William Beavis; Kendall Lamkey; and Anthony Assibi Mahama
Most cultivar improvement programs involve selection for multiple traits. Depending on the program or project goals, one of three types of multiple-trait selection can be employed. A brief description of these types follows.
- Multistage selection: Selection for different traits at different stages during cultivar development.
- Tandem selection: Selection for one trait until that trait is improved, then for a second, etc., until finally each has been improved to the desired level.
- Independent culling levels: A certain level of merit is established for each trait, and all individuals below that level are discarded regardless of values for other traits.
- Index selection: Select for all traits simultaneously by using some index of net merit.
- Explain the role of selection for multiple traits on genetic gain.
- Learn methods for selecting multiple traits.
- Learn how to evaluate the efficiency and effectiveness of selection on multiple traits.
Index Selection
An index is the best linear prediction of an individual’s or line’s breeding value and takes the form of the multiple regression of breeding value on all sources of information.
The objective of an index is to find the linear combination of phenotypic values that maximizes the expected gain or, equivalently, that maximizes the correlation between the index value and true worth (breeding value).
Index Selection Theory
Define phenotype as affected by components in Equation 1.
[latex]P_i = G_i + E_i (i = 1, ...,n)[/latex]
[latex]\textrm{Equation 1}[/latex] Linear model for sources of variability in phenotype.
where:
[latex]P_i[/latex] = the observed value of the attribute 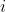 for an individual or line,
for an individual or line,
[latex]G_i[/latex] = the average of phenotypic values over a population of environments,
[latex]E_i[/latex] = non-genotypic contributions from environments.
Note: Genotype x environment interactions are permitted, assuming genotypes and environments are associated entirely at random; such interactions are incorporated into Ei (Equation 1). If GxE are not random, then see Cooper and DeLacy (1994).
Assume Gi is composed entirely of additive effects of genes (breeding values). Define the genotypic economic value, H, of an individual as written in Equation 2:
[latex]H = \sum^n_{i =1} a_i G_i[/latex]
[latex]\textrm{Equation 2}[/latex] Linear model for sources of variability in phenotype.
where:
[latex]a_i[/latex] = known relative economic values.
Assume the quantities Pi and H are such that the regression of Pi on H is linear. Selection will then be based on the linear function, I (Equation 3).
[latex]I = \sum^n_{i=1}b_iP_i = \sum^n_{i=1}b_i(G_i + E_i)[/latex]
[latex]\textrm{Equation 3}[/latex] Linear model for index selection.
where:
[latex]b_i[/latex] = regression coefficient,
[latex]\small P_i, G_i, E_i[/latex] are as defined previously.
Assumptions
Assume an equal amount of information on all individuals to be evaluated and selected. Also, assume that the distributions of Pi, Gi, and Ei are unknown but that the mean and covariances are known.
Then,
[latex]P_i \tilde{} NID(0, ^P\sigma_{ii}) (i = 1, ... , n) \\ G_i \tilde{} NID(0, ^G\sigma_{ii}) (i = 1, ... , n) \\ E_i \tilde{} NID(0, ^E\sigma_{ii}) (i = 1, ... , n) \\ Cov(G_i, E_i) = \ 0 \ (i=1, ... , n) \\ Cov(P_i, G_i) = \ ^G\sigma_{ii} (i=1, ... , n) \\ Cov(P_i, E_i) = 0 \ (i=1, ... , n) \\ Cov(P_i, P_j) = \ ^P\sigma_{ij}\ (i=j=1, ... , n) \\ Cov(G_i, G_j) = \ ^G\sigma_{ij} \ (i=j=1, ... , n) \\ Cov(E_i, E_j) = \ ^E\sigma_{ij}\ (i=j=1, ... , n)[/latex]
Mean and Covariance of H and I
With these assumptions, we can derive the mean and covariance of H and I as in the set of equations written in Equation 4.
[latex]E(H) = \sum^n_{i=1}a_iE(G_i) = 0, \quad V(H) = \sigma^2_H = \sum^n_{i=1}\sum^n_{j=1}a_ia_j\ ^G\sigma_{ij}[/latex]
[latex]E(I) = \sum^n_{i=1}b_iE(P_i) = 0, \quad V(I) = \sigma^2_I = \sum^n_{i=1}\sum^n_{j=1}b_ib_j\ ^P\sigma_{ij}[/latex]
[latex]Cov(I,H) = \sigma_{_{IH}} = \sum^n_{i=1} \sum^n_{j=1}a_ib_j \ ^G\sigma_{ij}, \quad Cov(G_i,I) = \sigma_{GiL} = \sum_jb_j ^G \sigma_{ij}[/latex]
[latex]\textrm{Equation 4}[/latex] Formulae for estimating mean, variance, and covariance of H, I, and Gi.
where:
terms are as defined previously.
The objective of a selection index is to use some linear combination of trait values (I) to predict true genetic worth (H).
This can be accomplished by:
- maximizing expected genetic gain.
- maximizing the correlation of the sample index (I) with true worth (H).
- maximizing the probability of correct selection.
- minimizing the E(I-H)2.
Williams (1962) showed that maximizing the correlation between I and H also maximizes the expected genetic gain and the probability of correct selection.
Derivation of the Optimum Index
Maximizing correlation of I with H (Equation 5):
[latex]r_{IH} = \frac{Cov(I,H)}{\sqrt{V(I)V(H)}} = \frac{\sum_i\sum_ja_ib_j \ ^G\sigma_{ij}}{\sqrt{(\sum_i\sum_jb_ib_j \ ^G\sigma_{ij})(\sum_i\sum_ja_ia_j \ ^G\sigma_{ij})}}[/latex]
[latex]\textrm{Equation 5}[/latex] Equation for estimating the correlation between I and H.
where:
terms are as defined in equation 4.
It can be shown that maximizing rIH is equivalent to maximizing log(rm ) (Equation 6).
[latex]\log{r_{_{IH}}} = \log{(\sum_i\sum_ja_ib_j\ ^G\sigma_{ij})} - {1 \over 2} \log{(\sum_i\sum_jb_ib_j\ ^P\sigma_{ij})} - {1 \over 2} \log{(\sum_i\sum_ja_ia_j\ ^G\sigma_{ij})}[/latex]
[latex]\textrm{Equation 6}[/latex] Equation for maximizing correlation of I with H.
where:
terms are as defined previously.
Using least squares and differentiating with respect to bj, we get Equation 7:
[latex]\frac{\partial \log{(r_{_{IH}})}}{\partial_{bj}} = \frac{\sum a_i\ ^G \sigma_{ij}}{\sigma_{IH}} - {1 \over 2}\frac{2 \sum_i b_i ^P \sigma_{ij}}{\sigma^2_I} = 0 \;\; (j = 1, ..., n), \;\; \frac{\sum_i b_i\ ^P \sigma_{ij}}{\sigma^2_I} = \frac{\sum_i a_i\ ^G \sigma_{ij}}{\sigma_{IH}} \;\; (j=1,...,n)[/latex]
[latex]\textrm{Equation 7}[/latex] Calculating the correlation of I with H using least squares techniques.
where:
all terms are as defined previously.
Rewriting the Normal Equations
These equations are called the normal equations (unrelated to normal distribution) and constitute n equations in n unknowns.
They can be rewritten as in Equation 8:
[latex]\sum_i b_i \ ^P\sigma_{ij} = \sum_i a_i\ ^G\sigma_{ij} (\frac{\sigma^2_I}{\sigma_{IH}}) \ j = (1, ...,n)[/latex]
[latex]\textrm{Equation 8}[/latex] Calculating the regression coefficient and observed value.
where:
all terms are as defined previously.
Because we are only interested in relative values of bi, the constant term can be dropped, resulting in Equation 9:
[latex]\sum_i b_i \ ^P\sigma_{ij} = \sum_i a_i \ ^G\sigma_{ij} \ j = (1,...,n)[/latex]
[latex]\textrm{Equation 9}[/latex] Dropping the constant values before calculating the regression coefficient and observed value.
where:
all terms are as defined previously.
Further Calculations
Considering 2 traits (n=2), Equation 9 is written as:
[latex]b_1 \; ^P \sigma_{11} + b_2 \ ^P\sigma_{21} = a_1 \ ^G\sigma_{11} + a_2 \ ^G\sigma_{21} \quad (j =1); \ b_2 \; ^P \sigma_{12} + b_2 \ ^P\sigma_{22} = a_1 \ ^G\sigma_{12} + a_2 \ ^G\sigma_{22} \quad (j =2)[/latex]
Solving the above equations, we get Equation 10:
[latex]b_1 = \frac{a_1[ ^G\sigma_{11}\ ^P \sigma_{22} - \ ^G\sigma_{12}\ ^P \sigma_{21}]+a_2[ ^G\sigma_{21}\ ^P \sigma_{22} - \ ^G\sigma_{22}\ ^P \sigma_{21}]}{ \ ^P \sigma_{11} \ ^P \sigma_{22}- \ ^P \sigma_{12} \ ^P \sigma_{21}}[/latex];
[latex]\ b_2 = \frac{a_1[ ^G\sigma_{12}\ ^P \sigma_{11} - \ ^G\sigma_{11}\ ^P \sigma_{12}]+a_2[ ^G\sigma_{22}\ ^P \sigma_{11} - \ ^G\sigma_{21}\ ^P \sigma_{11}]}{ \ ^P \sigma_{11} \ ^P \sigma_{22}- \ ^P \sigma_{12} \ ^P \sigma_{21}}[/latex].
[latex]\textrm{Equation 10}[/latex] Calculating the regression coefficient,
where:
all terms are as defined previously.
Minimizing E(I-H)2
The same equations can be derived to get Equation 9 by minimizing E(I-H)2 as written below:
[latex]E(I-H)^2 = E\Big[(\sum_ib_iP_i)-(\sum_ia_iG_i)\Big]^2 \\ E(\sum_ib_iP_i)^2 - 2E\Big[(\sum_ib_iP_i)(\sum_ia_iG_i)\Big] +E(\sum_ia_iG_i)^2 \\ \sum_i \sum_j b_ib_j \ ^P \sigma_{ij} - 2\sum_i \sum_j a_ib_j \ ^G \sigma_{ij} + \sum_i \sum_j a_i a_j \ ^G \sigma_{ij}[/latex]
because,
[latex]E(\sum_ib_i P_i)^2 = V(I); \ E\Big[(\sum_ib_iP_i)(\sum_i a_i G_i)\Big] = Cov(I,H); \ E(\sum_i a_i G_i)^2 = V(H)[/latex]
Applying least squares:
[latex]\frac{\partial E(I-H)^2}{\partial _{ij}} = 2 \sum_i b_i \ ^P \sigma_{ij} - 2 \sum_i a_i \ ^ G \sigma_{ij} = 0 \ (j= 1, ... , n)[/latex]
Dividing through by 2 and rearranging, we get the normal equations:
[latex]\sum_i b_i \ ^P \sigma_{ij} = \sum_i a_i \ ^ G \sigma_{ij}\ \ j= (1,...,n)[/latex]
which are identical to the equations presented previously.
Expected Genetic Gains
To derive the expected genetic gains, we need to make assumptions about the distributions of [latex]P_i[/latex], [latex]G_i[/latex], and [latex]E_i[/latex].
Assume:
- [latex]P_i[/latex], [latex]G_i[/latex], and [latex]E_i[/latex] are distributed normally with the mean and covariance structure given earlier.
- Truncation selection on [latex]I[/latex].
Then, the expected genetic gain is estimated with Equation 11:
[latex]\Delta H = E(\bar{H}_S - \bar{H}) = \beta_{HI}(\bar{I_S}- \bar{I})[/latex]
[latex]\textrm{Equation 11}[/latex] Calculating the genetic gain of change in genetic worth,
where:
[latex]\Delta H[/latex] = the genetic gain, that is, the change in genetic worth,
[latex]\beta_{HI}[/latex] = the regression coefficient of H on I, which gives the mean value of H or any value of I.
This is the standard way to calculate predicted gains from univariate selection. See, for example, Empig et al. (1972).
Truncation Selection
The situation with regard to truncation selection is based on the following where,
Ī is the mean value of the index in the population; c is the truncation point; z is the height of ordinate of the standard normal curve at the truncation point c;
P is the proportion of the population selected, and Īs is the mean of the selected individuals.
Then, the value of the frequency of the index is estimated with Equation 12:
[latex]f(I) = \frac{1}{\sigma_I\sqrt{2\pi}}e^{-[\frac{(I-\bar{I})^2}{2 \sigma^2}]}[/latex]
[latex]\textrm{Equation 12}[/latex] Calculating the genetic gain of change in genetic worth,
where:
[latex]f(I)[/latex] = the frequency of individuals with index value I
[latex]\textrm{other terms}[/latex] are as defined previously.
Selection Relationships
The proportion saved is related to the truncation point by [latex]S = \int_{c}^{\infty}f(I)\partial I[/latex], and the mean value of the selected group is [latex]\bar{I_S} = {1 \over S} \int_{c}^{\infty}If(I)\partial I[/latex].
The selection differential (D) is given by Equation 13:
[latex]D=(\bar{I_S} -\bar{I})={1 \over S}\bigg[\int_{c}^{\infty}If(I) \partial I - \bar{I}\bigg] = {1 \over S} \int_{c}^{\infty}(I - \bar{I})f(I) \partial I[/latex]
[latex]\textrm{Equation 13}[/latex] Formula for calculating the selection differential, D,
where:
[latex]S, I[/latex] are as defined previously.
Standardized Regression Coefficient
Let,
[latex]i = \frac{I - \bar{I}}{\sigma_I};\ c = \frac{C - \bar{I}}{\sigma_I};\ \partial i = \frac{\partial I}{\sigma_I}[/latex];
then, the standardized regression coefficient is derived as in Equation 14:
[latex]DD = \frac{\sigma_I}{S} \frac{1}{\sqrt{2\pi}} \int_{c}^{\infty} ie^{-[\frac{i^2}{2}]}[/latex];
[latex]\partial i = \frac{\sigma_I}{S} \frac{1}{\sqrt{2\pi}}e^{-[{c^2 \over 2}]}[/latex];
[latex]\ D = \frac{\sigma_i}{s} z[/latex]
[latex]\textrm{Equation 14}[/latex] Calculating the standardized regression coefficient,
where:
[latex]z[/latex] = the height of the ordinate at the truncation point.
Typically, this is represented as [latex]\frac{S}{\sigma_I} = \frac{z}{P} = i[/latex], where, k is the standardized regression coefficient.
Expected Gain
Expected gain can then be represented as in Equation 15:
[latex]\Delta H = kb_{HI}\sigma_{_I}[/latex],
[latex]\textrm{Equation 15}[/latex] Formula for expected genetic gain,
where:
[latex]\quad B_{HI} = \frac{Cov(H,I)}{\sigma_I^2}[/latex],
[latex]\quad Cov(H, I) \sum_i \sum_j a_i b_j \ ^G \sigma_{ij} = \sum_i b_j \sum_i a_i \ ^G \sigma_{ij}[/latex]
From the normal equations derived earlier, we have [latex]\sum_i b_i \ ^P \sigma_{ij} = \sum_i a_i \ ^G \sigma_{ij} \;\;\;\ j = (1,...,n)[/latex]
Substituting these terms,
[latex]Cov(H,I) = \sum_j b_j \sum_i b_i \ ^P \sigma_{ij} = \sum_i \sum_j b_i b_j \ ^P\sigma_{ij}; \ Cov(H,I) = \sigma^2_I[/latex], we get expected genetic as written in Equation 16:
[latex]\Delta H = \frac{kCov(H,I)}{\sigma^2_I}\sigma_I = k \frac{\sigma^2_I}{\sigma^2_I}\sigma_I = k \sigma_{_I}[/latex],
[latex]\textrm{Equation 16}[/latex] Alternative formula for expected genetic gain,
where:
[latex]terms[/latex] are as defined previously.
Predicted Gain
The predicted gain is more useful when written in terms of the correlation between H and I designated as rHI (Equation 17):
[latex]\Delta H = \frac{kr_{_{IH}} \sigma_{_H}\sigma^2_{_I}}{\sigma^2_I} = kr_{_{IH}}\sigma_{_H}[/latex],
[latex]\textrm{Equation 17}[/latex] Formula for predicted genetic gain,
where:
[latex]r_{{HI}} = \frac{Cov(H,I)}{\sigma_I \sigma_H} = \frac{\sigma_I}{\sigma_H}[/latex], as defined previously.
In the selection index literature, rHI is called the accuracy of selection because it is a measure of how well the index, I, measures the true worth, H.
Alternative selection indices, I, can be compared using rHI as long as the selection goal, H, remains the same for each of the indices.
Expected Genetic Gains for Each Trait
Let ΔGi be the expected genetic gain in trait i when selection is on I. From representations in previous equations as below, the expected genetic gains can be obtained as written in Equation 18.
[latex]\Delta H = \sum_i a_i \Delta G_i[/latex],
[latex]\textrm{Equation 18}[/latex] Formula for expected genetic gains for each trait,
where:
[latex]\Delta G_i = kB_{GiI} \sigma_{_I} (i=1,...,n) = k \frac{Cov(G_i, I)\sigma_I}{\sigma^2_I}(\frac{ \ ^G \sigma_{ii}}{\ ^G \sigma_{ii}}) =k \frac{Cov(G_i, I)}{ \sigma_{I}\ ^G \sigma_{ii}} \ ^G \sigma_{ii} = kr_{GiI}\ ^G \sigma _{ii}[/latex],
[latex]Cov(G_i, I) = E[G_i, \sum_j b_jP_j] = \sum_j b_j \ ^G \sigma_{ii}[/latex],
[latex]\sum_i a_i \textrm{Cov}(G_i, I) = \sum_i \sum_j a_i b_j \ ^G \sigma_{ij} = \textrm{Cov}(H,I)[/latex].
This index requires that you know the true values of the population parameters. However, estimates of the population parameters are often substituted for the true values, and the resulting index is called the estimated index or the Smith-Hazel index.
Matrix Representation of Selection Indices
With this notation, the normal equations can be written as [latex]Pb = Ga, and \ b = P^{-1}Ga[/latex].
Some Results
[latex]\sigma^2_I = \underline{b'}P\underline{b};\;\ \sigma^2_H = \underline{a'} G \underline{a};\;\ \sigma_{IH} = b'Ga = b'Pb = \sigma^2_I; \ \textrm{Cov} (G_i, I) = \sigma_{GiI} = b'G_i,[/latex]
where G_i is the ith row of G. The genetic gain can be written as in Equation 19:
[latex]\Delta H = k \sigma_I = k \sqrt{\underline{b'}P\underline{b}};\;\;\;\ \underline{\Delta} = \begin{pmatrix} \Delta G_1 \\ \Delta G_2 \\ \vdots \\ \Delta G_n\end{pmatrix};\;\ \Delta = \frac{G\underline{b}}{\sqrt{\underline{b'}P \underline{b}}};\;\;\ \Delta H = \underline{a'}\ \underline{\Delta}[/latex],
[latex]\textrm{Equation 19}[/latex] Matrix notation for expected genetic gains,
where:
[latex]r_{_{IH}} = \sqrt{f\frac{\underline{b'}G\underline{a}}{\underline{a'}G\underline{a}}}[/latex],
other terms are as defined previously.
Construction of a Selection Index
Optimum Index
The normal equations can be written for an optimum index as [latex]P \underline{b} = G \underline{a};\ \underline{b} = P^{-1}G \underline{a}[/latex],
where P, G, and a are known without error, and the index is as in Equation 20:
[latex]I = b'\underline{x};\ H = \underline{a'}\ \underline{y}[/latex],
[latex]\textrm{Equation 20}[/latex] Formula for optimum index,
where:
[latex]x[/latex] = trait x,
[latex]y[/latex] = trait y.
Smith-Hazel Index
This index is the same as the optimum index; only in this case (Equation 21), we use estimates of P, G, and a, designated as [latex]\hat{P}[/latex], [latex]\hat{G}[/latex], and [latex]\hat{a}[/latex], respectively.
[latex]\hat{P}\underline{\hat{b}} = \hat{G}\hat{\underline{a}};\;\ \hat{\underline{b}} = \hat{P}^{-1} \hat{G} \hat{a};\;\ \hat{I} = \hat{b'} \underline{x};\ H = \underline{\hat{a'}} \underline{y}[/latex],
[latex]\textrm{Equation 21}[/latex] Formula for Smith-Hazel index,
where:
[latex]terms[/latex] are as defined previously.
Base Index
The Base Index was apparently first suggested by Brim et al. (1959) and named the Base Index by Williams (1962). The base index is constructed simply by allowing b = a and written as in Equation 22, with all terms defined earlier.
[latex]I = \underline{a'} \underline{x};\;\;\ H = \underline{a'} \underline{y}[/latex],
[latex]\textrm{Equation 22}[/latex] Formula for Smith-Hazel index,
Some results for this index include:
[latex]\sigma^2_I = \underline{a'}P \underline{a};\;\ \sigma^2_H = \underline{a'} \underline{a};\;\; \textrm{Cov} (I,H) = \underline{a'} G \underline{a};\;\ r_{_{IH}} = \frac{\underline{a'}G\underline{a}}{\sqrt{(a'Pa)(a'Ga)}} = \sqrt{\frac{\underline{a'}G\underline{a}}{\underline{a'}P\underline{a}}}[/latex]
The foremost attribute of this index is its simplicity of construction and interpretation. Also, this index does not require the estimation of genetic parameters.
Multiplicative Index
The multiplicative index was first proposed by Elston (1963). This index is also sometimes called the weight-free index because it does not require the specification of index weights or economic values.
The general form of this index is as in Equation 23:
[latex]I = (X_1 - k_1)(X_2 - k_2) \cdots (X_n - k_n)[/latex],
[latex]\textrm{Equation 23}[/latex] Formula for multiplicative index,
where:
[latex]k_{1}[/latex] = the minimum value of trait X1 set by the breeder.
In addition to being weight-free, this index also does not require the estimation of genetic or phenotypic parameters. Because this is a curvilinear index, theory is not available to predict gains. Baker (1974) found that this index can be approximated by using a linear index, where the weights are the reciprocals of the phenotypic standard deviations of the traits in the index. This essentially amounts to an index with equal weighting per phenotypic standard deviation. Approximate, predicted gains can then be obtained for this index using the Smith-Hazel index theory.
Desired Gain Index
The desired gain index was suggested by Pesek and Baker (1969). This index allows the breeder to specify a vector of desired gains, [latex]\underline q[/latex], and then substitute this into the predicted gain equation and solve for  the index weights. The solution for [latex]\underline b[/latex] is as in Equation 24:
the index weights. The solution for [latex]\underline b[/latex] is as in Equation 24:
[latex]\underline{b} = G^{-1} \underline{q}[/latex],
[latex]\textrm{Equation 24}[/latex] Formula for desired gain index,
where:
[latex]\underline{q}[/latex] = the vector of desired gains,
[latex]I = \underline{b'x}[/latex] is as defined previously.
This index was proposed to eliminate the need to specify economic weights. However, in practice, there are some difficulties with the index in specifying the vector of desired gains.
This index will result in maximum gains in each trait according to the relative importance assigned by the breeder in specifying the desired gains.
Predicted gains can be obtained by substituting the vector of index weights into the conventional Smith-Hazel predicted gain equations.
Restricted Selection Index
Restricted selection indices were first derived by Kempthorne and Nordskog (1959). Since then, various restricted indices have been derived by Cunningham et al. (1970) and James (1968). See Lin (1978) for a complete list. Basically, restricted selection indices involve holding the genetic gains in one or more traits to a constant or zero while changing the means of other traits in the desired direction. The basic method is to impose the restriction on the index equations that [latex]Cov(G_i, I) =0[/latex].
The simplest procedure to accomplish this was given perhaps by Cunningham et al. (1970). Their method involved solving the following set of equations in Equation 25:
[latex]\begin{pmatrix} P &G_i \\ G_i &O \end{pmatrix}\begin{pmatrix} \underline{b} \\ \underline{b_d} \end{pmatrix} = \begin{pmatrix} G \\ O \end{pmatrix}[a][/latex],
[latex]\textrm{Equation 25}[/latex] Formula for restricted selection index,
where:
[latex]b[/latex] = [latex][I - P^{-1} G_i (G'_i P^{-1} G_i)^{-1}G'_i]P^{-1}G\underline{a}[/latex],
[latex]b_{d}[/latex] = [latex]\underline{b_d} = (G'_iP^{-1}G_i)^{-1} G'_i P^{-1} G \underline{a}[/latex],
[latex]\textrm{other terms}[/latex] are as defined previously.
b is the vector of index weights to use in the index equation as [latex]I=\underline{b'x}[/latex], as before. The dummy variable is not used in the index equation.
This method has the interesting consequence that the value obtained for the dummy variable is the negative of the economic weight needed to produce zero change in that trait in an unrestricted selection index.
Rank Summation Index
The rank summation index was first suggested by Mulamba and Mock (1978). Basically, this index involves obtaining the ranks of each of the traits to be included in the index and then calculating the index by summing up the trait ranks, represented in Equation 26.
[latex]I = \sum_{i=1}^{n} \textrm{rank} (X_i).[/latex]
[latex]\textrm{Equation 26}[/latex] Formula for the rank summation index,
where:
[latex]terms[/latex] are as defined previously.
The primary advantages of this index are that genetic parameters need not be calculated, it transforms the data so that the variances for each trait are identical, and it does not require the specification of economic weights, although they can be used.
As with the multiplicative index, predicted gains cannot be calculated for this index. However, Crosbie et al. (1980) found that the same prediction equation used for the multiplicative index provides a reasonably good approximation of the predicted gains for the rank summation index.
Selection Index Efficiency
Methods to Compare Selection Index Efficiency
Cunningham (1969) provided a method for comparing the relative efficiencies of selection indices. He was primarily interested in deleting traits from the index so that their relative contribution to the gain in the true worth (H) could be determined. Dropping traits from the index means that fewer genetic parameters need to be estimated, providing considerable cost savings.
Define the index containing all the traits of interest as the original index and define the index with one trait dropped out as the ith reduced index. Then the efficiency of the ith reduced index relative to that of the original index is the ratio of their standard deviations. Cunningham showed this to be as in Equation 27:
[latex]\sqrt{\frac{\underline{b'}P\underline{b} - {b_i^2 \over W_{ii}}}{\underline{b'}P \underline{b}}}[/latex]
[latex]\textrm{Equation 27}[/latex] Formula for selection index efficiency,
where:
[latex]b_{i}[/latex] = the ith weighting factor in the original index,
[latex]W_{ii}[/latex] = the corresponding diagonal element in the inverse of P.
A more usual procedure is to compare the gain for the ith trait when selection is on I, relative to the single trait selection for the ith trait.
Effect of Correlations on Index Weights
To determine the effects of correlation on index weights, we need to derive the index equations Pb = Ga in terms of genetic and phenotypic correlation coefficients (Equations 28, 29, 30) following the series of derivations as follows. Let,
[latex]X^*_i = \frac{X_i}{\sqrt{\ ^P \sigma_{ii}}} = \frac{G_i + E_i}{\sqrt{\ ^P \sigma_{ii}}} \space (i=1,...,n) \\ \text{Then:} \\ V(X^*_i) = \ ^P\sigma_{ii} = 1 \\ \textrm{Cov}(X^*_i, X^*_j) = \frac{\ ^P \sigma_{ij}}{\sqrt{\ ^P \sigma_{ii}\ ^P \sigma_{ij}}} = \ ^P r_{ij} \space (i=j=1,...,n) \\ V(G^*_i) = V(\frac{G_i}{\sqrt{\ ^P \sigma_{ii}}})= \frac{\ ^G \sigma_{ii}}{\ ^P \sigma_{ii}} = h_i^2 \\ Cov(G^*_i, G^*_j) = \frac{\ ^G \sigma_{ij}}{\sqrt{\ ^P \sigma_{ii} \ ^P \sigma_{jj}}} = h_{ij}[/latex]
Derivation
[latex]P^* = \begin{pmatrix} 1 &^P r_{12} &\cdots & ^P r_{1n}\\ ^P r_{21} &1 &\cdots & ^P r_{2n} \\ \vdots &\vdots & \ &\vdots \\ ^P r_{n_1} & ^P r_{n_2} &\cdots &1\end{pmatrix};\;\ G^* = \begin{pmatrix} h_{11} &h_{12} &\cdots & h_{1n}\\ h_{21} &h_{22} &\cdots &h_{2n} \\ \vdots &\vdots & \ &\vdots \\ h_{n1} &h_{n2} &\cdots &h_{nn}\end{pmatrix};\;\ \underline{\hat{b}}^* = (P^*)^{-1} G^* \underline{a}[/latex]
[latex]\textrm{Equation 28}[/latex] Formula for phenotypic and genotypic correlations,
where:
[latex]terms[/latex] are as defined previously.
For 2 traits (n=2),
[latex]\underline{\hat{b}}^* = \begin{pmatrix} a_1 ({h_1}^2 - \ ^Pr_{12}h_{12}) + a_2 (h_{12} - \ ^Pr_{12}{h_2}^2) \\ a_1 (h_{12} - \ ^Pr_{12}{h_1}^2) + a_2 ({h_2}^2 - \ ^Pr_{12}{h_{12}}) \end{pmatrix}(\frac{1}{1-(\ ^Pr_{12})^2})[/latex]
[latex]\textrm{Equation 29}[/latex] Formula for estimated correlation between two traits,
where:
[latex]terms[/latex] are as defined previously.
When correlations are zero: Pr12 = Gr12 = 0,
[latex]\hat{b}^* = \begin{pmatrix} a_1h_1^2 \\ a_2h_2^2 \end{pmatrix};\;\;\ P = \begin{pmatrix} \ ^P\sigma_{11} &0 \\ 0 &\ ^P\sigma_{22} \end{pmatrix};\;\;\ P^{-1} = \begin{pmatrix} \frac{1}{\ ^P\sigma_{11}} &0 \\ 0 &\frac{1}{\ ^P\sigma_{22}} \end{pmatrix};\;\;\ G = \begin{pmatrix} \ ^G\sigma_{11} &0 \\ 0 &\ ^G\sigma_{22} \end{pmatrix}[/latex]
[latex]\textrm{Equation 30}[/latex] Formula for estimated correlation between two traits when phenotypic and genetic correlations are zero,
where:
[latex]terms[/latex] are as defined previously.
When | r | < 0.30, the use of the above index is nearly as efficient as using the Smith-Hazel index.
References
Brim, C. A., H. W. Johnson, and C. C. Cockerham. 1959. Multiple selection criteria in soybeans. Agron J 51: 42-46.
Crosbie, T. M., J. J. Mock, and O. S. Smith. 1980. Comparison of gains predicted by several selection methods for cold tolerance traits in two maize populations. Crop Sci. 20:649-655.
Cunningham, E. P. 1969. The relative efficiencies of selection indexes. Acta Agriculturae Scandinavica 19(1): 45-48.
Elston, R. C. 1963. A weight-free index for the purpose of ranking or selection with respect to several traits at a time. Biometrics 19(1): 85-97.
James, J. W. 1968. Index selection with restrictions. Biometrics 24, 1015-1018.
Kempthorne, O., and A. W. Nordskog. 1959. Restricted selection indices. Biometrics 15:10-19.
Lin, C. Y. 1978. Index selection for genetic improvement of quantitative characters. Theoretical and Applied Genetics, 52(2): 49-56.
Mulamba, N N., and J. J. Mock. 1978. Improvement of yield potential of the Eto Blanco maize (Zea mays L.) population by breeding for plant traits. Egypt. J. Genet. Cytol. 7: 40-51.
Pesek. J., and R. J. Baker. 1969. Desired improvement in relation to selection indices. Can J Plant Sci, 9: 803–804.
Williams, J. S. 1962. The evaluation of a selection index. Biometrics 18:375-393.
How to cite this module: Beavis, W., K. Lamkey, and A. A. Mahama. 2023. Multiple Trait Selection. In W. P. Suza, & K. R. Lamkey (Eds.), Quantitative Genetics in Plant Breeding. Iowa State University Digital Press.

