Chapter 7: Marker Assisted Selection and Genomic Selection
Thomas Lübberstedt; William Beavis; and Walter Suza
Marker-assisted selection (MAS) was applied as early as the 1980s when Tanksley and Rick (1980) used isozymes as markers for introgression of an exotic trait into adapted tomato cultivars. The premise behind use of markers is that selection on genotype rather than phenotype may increase speed and efficiency of selection. As you learned in the previous lesson, marker-assisted backcrossing (MABC) involves the use of markers to help recover the genome of the donor parent during a backcrossing program. In contrast, marker-assisted selection (MAS) aims to develop improved novel genotypes that are likely quite different from parental genotypes, based on markers that represent quantitative trait loci (QTL) alone (marker-based selection, MBS), or in combination with phenotypic selection, which was the original definition of marker-assisted selection (MAS) by Lande and Thompson (1990). MAS is sometimes used as summary term for application of markers in connection with selection procedures.
MAS and MBS are used to generate new lines or populations, whereas MABC is used to improve existing lines by adding one or few genes. During MAS and MBS, a breeder intermates combinations of complementary elite lines to identify transgressive segregants for multiple genes/alleles. Marker information is usually based on preceding QTL mapping experiments. This can be critical, if QTL/marker information is based on different genotypes in the mapping experiment compared to the breeding program. As different combinations of QTL segregate in different populations, the transferability of information across populations is limited. Markers would ideally be diagnostic for the presence of beneficial QTL alleles and thus valid across numerous crosses.
MAS has been shown to be more efficient than conventional phenotypic selection for traits with low heritability, and some of the MAS strategies have been successfully implemented in breeding programs of Monsanto® and other companies for different species. The following sections will discuss MAS strategies, efficiency, and factors that influence MAS and alternative approaches to MAS that can be applied in a breeding program.
- Understand difference between marker-assisted backcrossing (MABC) and marker-assisted selection (MAS).
- Develop an awareness of the relative efficiency of MAS versus phenotypic selection.
- Understand factors that influence efficiency and limitations of MAS.
- Understand MAS strategies.
- Develop an awareness of the alternative approaches to MAS.
- Understand differences between Marker-Assisted Selection (MAS) and GS
- Understand principles of Genomic Selection (GS).
Limitations in QTL Mapping
QTL Dependencies
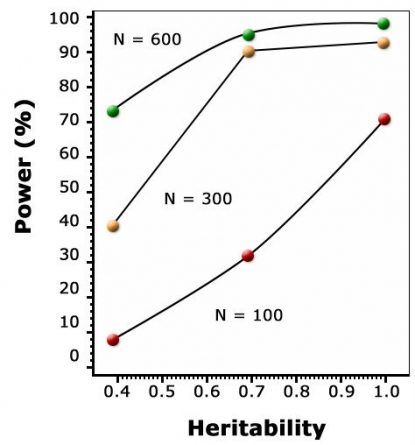
As discussed in the module on Cluster Analysis, Association & QTL Mapping, the goal of QTL mapping is to identify one or more genomic region(s) called quantitative trait locus (QTL) controlling a particular trait. However, the statistical power for detecting QTL depends on population size, leading to overestimation of QTL effects in small populations (Beavis, 1994), the Beavis effect. For this reason, QTL studies depend on very large sample sizes, and are only capable of detecting differences that are captured between the parents used to form a mapping population. Thus, within a given population, if the same parents were used to map QTL and to establish a breeding population, all QTL are of interest. Some QTL might not be relevant when they are transferred to other populations (if there is no segregation for that QTL). Another issue is, QTL determined at per se level might not be relevant for the testcross level in hybrid species like maize. Therefore, the way phenotyping is done affects the detection and consistency of QTL.
For all strategies presented in this lesson, it is crucial to understand that the reason for limited success of MAS (compared to GS) is their dependence on QTL mapping. QTL mapping has been shown to only find a fraction of QTL affecting a quantitative trait, and to overestimate genetic effects for detected QTL. Thus, during MAS, relevant regions in the genome are missed, whereas other regions likely get too much weight, so that expected findings likely differ from actual ones, leading to limited gain in selection.
Impact Graph
MAS Strategies
MAS Strategies – F2 Enrichment
A. F2 Enrichment
The objective of the F2 enrichment strategy is to develop superior Recombinant Inbred Lines (RILs). MAS is particularly useful for F2 individuals or F2-derived lines, or other early generations (DHs, BC1-derived populations), because LD between marker loci and the trait of interest are at a maximum in a segregating population. A good example of the application of F2-enrichment comes from a wheat breeding program at CSIRO Plant Industry in Canberra, Australia (Bonnett et al., 2004).
The F2 enrichment procedure involves:
- QTL identification
- Culling of undesirable genotypes to increase frequency of desirable alleles/genotypes
- Identification of RILs with all favorable QTL alleles fixed
[latex]y = \mu _{\mathit{0}} + \sum_{\mathit{i=1}}^{N}a_{i}x_{i}+\varepsilon[/latex]
where:
y = the expected phenotypic value of an individual
μ0 = the model mean
ai = additive effect of the marker.
ε = random environmental factor
xi= indicator variable (with values 1,0 and -1 for marker genotypes MM, mm, and mm)
N = the number of markers
Obtaining Marker Scores
B. Use of Marker Scores in Selection
Theoretically, selection of individuals is most efficient when based on additive gene effects. QTL analysis identifies chromosome segments affecting traits of interest, and enables us to estimate gene effects (additive, dominance, and epistasis) for each QTL. If summarized across all detected QTL, the expected performance of an individual can be predicted based on the QTL information. QTL analysis depends on the precise mapping of each QTL along with marker-trait regression analysis to estimate the genetic effects of QTL. Marker-trait regression uses the following equation:
[latex]y = \mu _{\mathit{0}} + \sum_{\mathit{i=1}}^{N}a_{i}x_{i}+\varepsilon[/latex]
where:
y = the expected phenotypic value of an individual
μ0 = the model mean
ai = additive effect of the marker.
ε = random environmental factor
xi = indicator variable (with values 1,0 and -1 for marker genotypes MM, mm, and mm)
N = the number of markers
Thus, markers (representing QTL) with significant effects on the trait of interest can be used to obtain marker scores (also referred to as molecular score) for each individual. The following expression is used to estimate marker scores (MS):
[latex]MS = \sum_{\mathit{\mathit{i=1}}}^{N}a_{i}x_{i}[/latex]
where:
n = the number of markers selected
ai = additive effect of the marker i
xi = indicator variable with values 1, 0 and -1 for marker genotypes MM, Mm and mm)
Derivation of a Selection Index
C. Derivation of a Selection Index for MAS
Lande and Thompson (1990) demonstrated that MAS is most effective when breeding values are predicted by an index of QTL genotypic values and phenotypic values. Index weights are estimated that maximize the correlation between the index and a candidate’s breeding value (Atotal). Atotal is the sum of individual’s breeding value for the marked QTL (AQTL) and the breeding value for all other genes (Arest), not explained by QTL. Thus, Atotal = AQTL + Arest.
- Estimating marker scores
A marker weight coefficient (bMS) is estimated as follows:
[latex]b_{MS} = \frac{1-h_{2}}{1-\Theta h_{2}}[/latex]
where:
MS = marker score
h2 = narrow sense heritability
θ = proportion of genetic variance explained by a marker score
- Estimating index weight of marker score relative to phenotype
An individual’s phenotype (P) is weighed using the following formula (Bernardo, 2009):
[latex]b_{p} = \frac {h^2(1 - \Theta )}{1-\Theta h^{2}}[/latex]
Thus, MS is weighted more heavily than P.
If h2 is 1, and θ ranges from 0.1 to 0.75, then the numerator of the marker weight coefficient bMS will be close to 0, and thus, almost no weight will be assigned to markers. Thus, the higher the heritability of a trait, the lower the marker score. On the other hand, if h2 is low, and if θ is if high (>0.5), more weight will be assigned to markers.
- Interpretation of the marker score
Assume a candidate’s breeding value (Atotal) is the sum of its breeding value for the marked QTL (AQTL) and its breeding value for all other genes (Arest), not explained by QTL:
Atotal = AQTL + Arest
Thus,
- The marker score gives an estimate of AQTL
- Phenotype can be used to estimate an individual’s total breeding value, Atotal
Therefore, possible selection strategies could be based on MS and phenotype as described by the following steps:
- Select on marker score alone: this ignores the information that is provided by phenotype on all the other genes that affect particular traits
- Independent culling level selection: that is, based on (a) selection on marker score, (b) selection on phenotype. Some individuals with desirable genes for non-marked QTL may be eliminated in (a)
- Index selection: develop index of marker score and phenotype (I = bMS MS + bp P). In general, expected response to selection index > independent culling > MS alone.
Marker-Assisted Recurrent Selection
D. Marker-Assisted Recurrent Selection
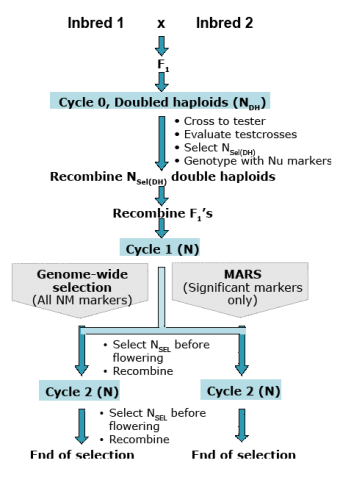
Marker-assisted recurrent selection (MARS) is used to enrich favorable alleles for QTL of interest over multiple generations. Indirect selection during winter generations can be combined with phenotypic selection or selection indices in rapid breeding cycles (Fig. 2).

MARS involves:
- QTL identification, similar to F2 enrichment.
- Identification of best individuals based on marker score (Table 1) within population.
- Recombination of best individuals followed by identification of best individuals as described in (2).
- Click here to learn more about the application of MARS: Agronomy.org MARS information
MAS Strategies Comparison
Similarities and Differences of MAS Strategies
| F2 enrichment | MARS |
| Involves QTL identification | Involves QTL identification |
| QTL are given equal weights | QTL are weighed according to the additive effect |
| Culling of undesirable genotypes | Identification of best individuals based on marker scores |
| Identification of RIL with favorable fixed alleles | Recombination of best individuals |
Efficiency of MAS
Selection Index
To understand, what determines efficiency of MAS, we must understand how it is estimated. First, we estimate the accuracy of selection based on the selection index theory.
The selection index (I) is used to account for the relative superiority or inferiority of individuals for all the traits represented by the index.
[latex]I = b_1X_1 + b_2X_2 + … + b_nX_n = Σb_iX_i[/latex]
where:
bi is the weight for trait i, and Xi is the phenotype value for trait i. The value of I is calculated for every individual or family in a population.
The selection index can also be denoted as I = bMM + bpP.
[latex]b_P = \frac{V_A - V_M}{V_P - V_M}[/latex]
[latex]b_M = \frac{V_P - V_A}{V_P - V_M}[/latex]
where:
bM and bp are weights, M (or MS) is the marker score, and P is the phenotypic value.
The following equations can be used to estimate bP and bM:
[latex]b_P = \frac{V_A - V_M}{V_P - V_M}[/latex]
[latex]b_M = \frac{V_P - V_A}{V_P - V_M}[/latex]
where:
VA = additive genetic variance
VM = the additive variance explained by the marker
VP = phenotypic variance
Estimating Relative Efficiency of MAS
Assuming that the selection intensity and generation interval are similar, the relative efficiency (RE) of MAS over phenotypic selection is obtained by comparing response from MAS to response from phenotypic selection (Bernardo, 2002).
- RE of marker-based selection (REMBS:PS)
[latex]RE_{MBS:PS} = \frac{\sqrt{\frac{V_M}{V_A}}}{h}[/latex]
- RE of marker-assisted selection (REMAS:PS)
[latex]RE_{MAS:PS} = \frac{\frac{V_M}{V_A}}{h^2} + \frac{{(1-(\frac{V_M}{V_A}))}^2}{1-h^2(\frac{V_M}{V_A})}[/latex]
Comparison to Phenotypic Selection
As Figure 3 and Table 1 show, MAS is more efficient than phenotypic selection for traits with low heritability, but MAS may not be economically justifiable for traits with higher heritability, and that are easier to score phenotypically. The reason is that when heritability (h) is high, gain from phenotypic selection nears the maximum possible given the genetic variance, leaving a small window for additional improvement by the use of markers.
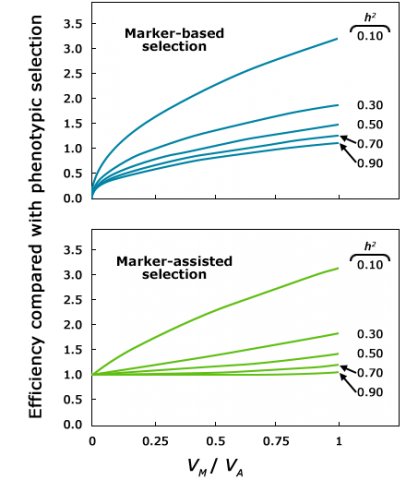
Factors Affecting Efficiency
| Trait | VM/VA | h2 | Relative Efficiency |
| Yield | 0.51 | 0.63 | 1.09 |
| Grain moisture | 0.55 | 0.94 | 1.00 |
| Stalk lodging | 0.62 | 0.39 | 1.33 |
| Root lodging | 0.62 | 0.39 | 1.33 |
| Plant height | 0.58 | 0.89 | 1.01 |
Therefore, many factors affect the efficiency of MAS, including the size of the QTL mapping population, the phenotype to be scored, experimental design and analysis, the number of markers available, the degree of association between available markers and the QTL, the proportion of additive effect described by the marker, and the selection method. Also, the crop to be improved and the marker development pipeline have a bearing on the efficiency of MAS. While MAS may provide greater relative efficiency than phenotypic selection, MAS programs also require higher economic efficiency to justify their application in a breeding program. As seen in Table 2, MAS is less economical for traits such as seedling emergence. Such traits may be easier to score visually and would thus not justify the use of MAS for their evaluation. On the other hand, biochemical traits such as sucrose concentration justify the application of MAS because they are difficult to score.
| C1 [latex]\ddagger[/latex] | C2 [latex]\S[/latex] | C3 [latex]\S[/latex] | ||||
| Trait | PS | MAS | PS | MAS | PS | MAS |
| Emergence | 56 | 103 | 42 | 78 | 37 | 70 |
| Sucrose | 178 | 164 | 134 | 109 | 119 | 90 |
| Tenderness | 158 | 154 | 119 | 104 | 105 | 87 |
| Hedonic rating | 370 | 260 | 278 | 157 | 247 | 122 |
| [latex]\dagger[/latex] Average costs of selecting and evaluating one family for each trait in the first cycle (C1) and in subsequent cycles (C2 to C3). [latex]\ddagger[/latex]Estimated costs based on actual responses. [latex]\S[/latex]Projected costs based on costs associated with PS and MAS in the first cycle of selection. |
||||||
Examples of Application in Crop Breeding
Example 1: Implementing MAS in Australian Wheat Breeding
The programs use DNA markers for selection for traits of high economic importance, which are controlled by single genes, and difficult to score reliably by non-marker assays (Eagles et al. 2001). In these programs, markers are also used for introgression of multiple genes controlling single traits (Lessons 4 and 5). Table 3 lists DNA markers used in wheat breeding in Australia.
Resistance to cereal cyst nematode (CCN) and tolerance to boron toxicity are difficult to phenotype. As shown in Table 3, two QTL have been identified for each of the two traits. The CCN markers are tightly linked to the resistance genes, and derived from germplasm sources outside the Australian wheat gene pool. Thus, markers for resistance to CCN have had greater success in stacking resistance in susceptible cultivars of wheat (Eagles et al. 2001). In contrast, the boron tolerance genes are present within Australian gene pool. For this reason, marker alleles for tolerance to boron are also observed in many susceptible lines in wheat breeding programs (Eagles et al., 2001), limiting their success as diagnostic tools for boron tolerance.
Example 2: Use of MAS in Breeding for Resistance to Soybean Cyst Nemotode
Soybean cyst nematodes (SCN) cause major economically important yield losses. The North American soybean germplasm pool lacks genes for resistance to SCN. The source of resistance to SCN is the center of soybean diversity in Asia. Resistance to SCN is controlled by one major gene, rhg1 and additional minor alleles (Cregan et al. 1999). Resistance to SCN is difficult to score reliably, warranting the use of MAS in selection for the trait. Novel marker alleles linked to SCN resistance genes have strong linkage disequilibrium to resistance genes. Also, the markers are reproducible consistently across multiple breeding populations. Since resistant progeny lines developed from resistant parents will also have the same marker alleles as their resistant parents, the markers can be used as diagnostic tools for resistance to SCN. Therefore, the markers will be useful in most future populations made by crossing resistant lines to susceptible lines.
The two examples underscore the importance of identifying markers that are tightly linked to target genes. Such markers are ideally developed from causal gene sequence to ensure that they are specific to the resistance allele, for example, the Cre genes for SCN resistance (Table 4). Marker alleles from different gene pools have a higher chance to be distinct and thus, diagnostic.
Example 3: Use of MAS In Introgression of Yield QTL Alleles in Soybean
Reyna and Sneller (2001) observed insignificant marker effects for yield QTL when a superior northern soybean cultivar was tested in southern environments. Therefore, MAS may not be useful in transferring superior genetic value of a cultivar to populations of environments in which the superior cultivar is not adapted. Such negative results from MAS are not always reported, resulting in publication bias for research that generates positive value of MAS in cultivar development.
Reasons for Varying Successes of MAS
In the case of polygenic traits such as yield MAS has produced mixed results. The reasons for less success of MAS in selection of polygenic traits include:
- Accurate estimation of location and effects of underlying QTL is difficult.
- Different QTL may be important in different populations.
- Phenotypic selection is already efficient for moderate to high heritability traits, making MAS less economical.
- QTL mapping methods require integration into efficient breeding procedures.
The above limitations to the success of MAS contribute to the “catch-22 of MAS” which means that if phenotypic data are poor indicators of genotypes, QTLs cannot be adequately mapped to implement MAS. On the other hand, if phenotypic data are good, MAS is not needed.
The Catch-22 of MAS can be avoided if a small number of QTL explain most of the genetic variation. In that case, high heritability in the QTL mapping phase is optimal to identify QTL markers. Then, markers can be implemented more economically than phenotyping in future selection cycles. Nonetheless, yield variation is not likely to be explained by few QTL, because underlying QTL will vary across populations.
Alternative Approaches to MAS
A. Mapping As You Go (MAYG)
The MAYG strategy re-estimates the value of QTL alleles as new germplasm is developed over breeding cycles (Podlich et al., 2004). In general, MAYG involves the following steps:
- Estimation of QTL effects in progeny of an initial set of crosses.
- Construction of marker alleles based on information from step 1 for MAS on germplasm.
- Creation of new set of crosses among selected lines.
- Update of the estimates of the QTL effects for use in the next selection cycle.
- Continuation of the process (1-5) using new estimates of QTL effects (Fig. 4).

B. Breeding By Design
Markers are useful in development of haplotype maps (see the eModule on Markers and Sequencing). Breeding by design requires information about chromosome haplotypes. Figure 5 below is an example of a haplotype map. Breeding by design describes the use of chromosome haplotypes to aid selection of F2 or BC individuals to develop superior elite line genotype.
Breeding by design describes the use of chromosome haplotypes to aid selection of F2 or BC individuals to develop superior elite line genotype.
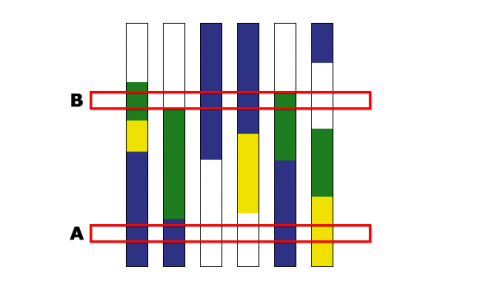
The Principle of Breeding by Design
In Fig. 6, three chromosomes, A, B and C, of five parental lines, 1-5 are indicated side by side. Selection of specific recombination points on chromosomes A and B are done and chromosome C is selected from parental line 1. Dotted lines delineate marker positions used to select for the desired recombinants. The genome composition of the ideal line with respect to the three chromosomes is indicated.

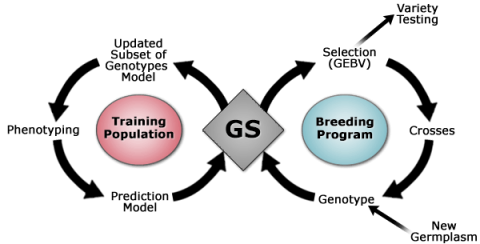
Genomic Selection
Advantage of Using GS
As discussed in previous sections, selection based on the genotype rather than the phenotype may result in faster and more efficient ways to conduct selection. However, the paradox of MAS makes detection of quantitative traits with low heritability less reliable because the power of detecting quantitative trait loci (QTL) depends on size of the mapping population and heritability of the trait. Also, application of MAS in small populations may lead to bias in magnitude of QTL effects and estimation of location of QTL. In contrast, Genomic Selection (GS) is a form of MAS involving estimation of the breeding values of lines in a population by evaluating their phenotypes and scores of markers that span the entire genome. The incorporation of all marker information in the GS prediction models helps avoid biased estimate of marker effects allowing the capturing of variation caused by small-effect QTL.
GS Principles
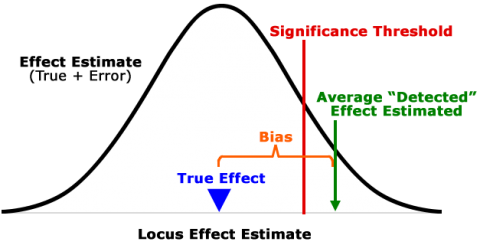
QTL studies detect in most cases only the “tip of the iceberg”, a limited number of QTL representing a small subset of all QTL affecting the trait(s) of interest. As QTL mapping employs a significance test, most true QTL are not detected (below significance threshold) (Fig. 7). Locus effect estimates of QTL that are detected are generally inflated (Fig. 7; “Beavis effect”).
Application of GS
The application of GS in plant breeding was first introduced in the early 2000 (Meuwissen et al., 2001) and is based on the following principles:
- Dense marker maps covering all chromosomes allow accurate estimation of breeding values of individuals that have no phenotypic record and no progeny.
- Estimation of breeding value requires large number of marker haplotype effects.
- Methods that are based on prior distribution of variance associated with each chromosome segment provide more accurate prediction of breeding values.
- Selection based on genomic estimated breeding value (GEBV) has potential to increase the rate of genetic gain (Fig. 8) when combined with reproductive techniques, for example, doubled-haploids.
Important Factors
In applying GS it is also important that:
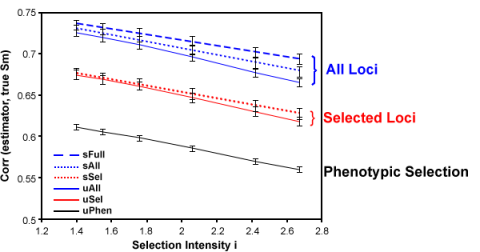
- All markers contribute to prediction, i.e. there is no distinction between “significant” and “non-significant” effects (Fig. 7). Thus, there is no arbitrary exclusion or inclusion of markers. The value of analyzing all loci is illustrated by Fig. 9.
- More effects are estimated than there are phenotypic observations.
- Smaller QTL effects are captured.
- Genetic relationships are captured.
- Multiple low cost markers are available.
Two Population Types
In GS, two types of populations are considered:
- Training population – Both genotypic and phenotypic data should be available allowing fitting of a large number of markers as random effects in a linear model to estimate all marker effects simultaneously. The aim is to capture all of the additive genetic variance caused by alleles with both large and minor effects
- Breeding population – Only genotypic data are required to allow estimates of marker effects for prediction of breeding values, and selection of lines with GEBV.
GS Methods
The Basic Model
Statistical methods used for GS include, stepwise regression, ridge regression best linear unbiased prediction (RR-BLUP), and Bayesian estimations (Heffner et al., 2009). The basic model (Habier et al., 2007) underlying these methods can be written as:
[latex]y = \mu + \sum_{k}^{} X_{h}\beta _{k}\delta _{k} + e[/latex]
where:
y = a vector of tarit phenotypes
μ = the overall mean
xk =a column vector of marker genotypes at locus k
βk = the marker effect
δk = a 0/1 – indicator variable
e = a vector of random residual effects
| Performance with increased | |||||||
| Method | Marker effect; variance assumption | Proportion of markers fitted in model | Marker density | QTL [latex]\dagger[/latex] density | Large-effect QTL | Small-effect QTL | Inbreeding depression; loss of diversity |
| Traditional BLUP | N/A | N/A | N/A | N/A | Captured only by phenotype | Captured only by phenotype | Yes |
| Stepwise regression | Fixed | Subset | Reduced | Reduced | Overestimated | Excluded | Marginally Reduced |
| RR-BLUP[latex]\ddagger[/latex] | Random; Equal | All | Reduced [latex]\S[/latex] | Increased | Underestimated | Captured | Reduced |
| BayesA | Random; Unique All>0 | All | ? | Reduced | More accurately estimated | Captured | Reduced |
| BayesB | Random; Unique Some=0 | All | Insensitive [latex]\S[/latex] | Reduced | More accurately estimated | Captured | Reduced |
| [latex]\dagger[/latex] QTL, quantitative trait locus. [latex]\ddagger[/latex] RR, ridge regression [latex]\S[/latex] Source: Fernando (2007). |
|||||||
Regression Models
The ability of GS to capture information on genetic relatedness is valuable. However, information on genetic relatedness decays rapidly. Importantly, the amount of information captured is strongly related to the number of markers fitted by a model. In estimating marker effects, two components contribute to an effect, these are, marker and error. When the effect is large, chances are that the error is also large. Thus methods that shrink (regress) the effects toward the mean as of a function of relative error and factor variances are used. Regression models (e.g., Bayesian) can partition contributions of linkage disequilibrium (LD) versus genetic relatedness. Thus regression models help and increase in long-term accuracy in estimating marker effects.
Marker Difference
In GS procedures, marker effects are considered to be random, in contrast to MAS, where marker effects are considered to be fixed effects. The differences between random and fixed marker effects are listed below.
Random markers
- Genome-wide markers
- Each effect considered as coming from a population of marker effects with a probability distribution
- Interested in predicting future values marker effects
- Hypothesis testing may be done on populations, which are considered static
- Estimation and prediction are important
- To predict, one needs to quantify influence of error relative to “factor processes”
- Dependence on population properties best addressed by random effect
Fixed markers
- They are developed from candidate loci
- Each locus is different biologically, i.e., there is no population
- Each candidate locus is a hypothesis
- Hypothesis testing based on effects
- Estimation and prediction are not important
- No particular interest in estimating effects as long as a hypothesis is tested
- Future values of effects are also not relevant.
Simulation Studies
GS vs. MARS Comparison
Simulation studies of testcross performance of doubled haploids in maize (Fig. 10) suggest that GS is more effective than MARS for complex traits under the control of many QTL with low heritability (Table 10). However, GS is less beneficial for recurrent selection for choosing parents of breeding populations or selection of single-crosses (Bernardo and Yu, 2007).
Responses to Different Selections
| Heritability | |||||
| Number of QTL | Method | Number of Markers | 0.20 | 0.50 | 0.80 |
| 20, 40, or 100 | Phenotypic selection | 0 | 1.60 |
2.26 | 2.61 |
| 20 | MARS | 32 | 2.50 (0.4) |
3.14 (0.4) | 3.38 (0.4) |
| 64 | 2.72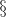 (0.3) (0.3) |
3.42 (0.4) | 3.73 (0.4) | ||
| 128 | 2.54 (0.3) | 3.47 (0.2) | 3.87 (0.4) | ||
| 256 | 2.26 (0.2) | 3.19 (0.2) | 3.72 (0.2) | ||
| Genomewide selection | 64 | 2.86 | 3.50 | 3.76 | |
| 128 | 2.98 | 3.67 | 4.02 | ||
| 256 | 3.06 | 3.72 | 3.98 | ||
| 512 | 3.05 | 3.68 | 4.10 | ||
| 768 | 3.06 | 3.73 | 4.05 | ||
| RGS:MARS¶ | 113% | 107% | 106% | ||
| R(GS-PS):(MARS-PS)# | 130% | 121% | 118% | ||
MAS Compared to GS
The similarities and differences between MAS and GS are shown in Figure 11. In general, MAS involves identification of alleles for development of markers for use in pre-selection of individuals containing an allele of interest. In contrast, GS does not require identification of genes as a source of markers for pre-selection of segregants with desirable alleles. Instead, whole chromosome segments are scanned to estimate the effect of QTL on a trait of interest.
References
Asoro, F. G., M. A. Newell, W. D. Beavis, M. P. Scott, and J-L. Jannick. 2011. Accuracy and Training population design for genomic
selection on quantitative traits in elite North American oats. Plant Genome 4: 132-144.
Bernardo, R. 2002. Breeding for quantitative traits in plants. Stemma Press, Woodburry.
Bernardo, R. 2008. Molecular Markers and Selection for Complex Traits in Plants: Learning from the Last 20 Years. Crop Sci.
48:1649-1664.
Bertrand, C. Y. C., and D. J. Mackill. 2008. Marker-assisted selection: an approach for precision plant breeding in the twenty-first century.
Phil. Trans. R. Soc. B 363:557-572.
Bernardo, R., J. Yu. Prospects for genomewide selection for quantitative traits in maize. Crop Sci. 47: 1082-1090.
Bonnett, D.G., G.J. Rebetzke, and W. Spielmeyer. 2005. Stratehgies for efficient implementation of molecular markers in wheat breeding. Mol. Breeding 15: 75-85.
Cregan, P. B., J. Mudge, E. W. Fickus, D. Danesh, R. Denny, and N. D. Young. 1999. Two simple sequence repeat markers to select for
soyben cyst nematode resistance conditioned by the rhg1 locus. Theor Appl Genet 99: 811-818.
Eagles, H.A., H. S. Bariana, F. C. Ogbonnaya, G. J. Rebetzke, G. J. Hollamby, R. J. Henry, P. H. Henschke, and M. Carter. 2001.
Implementation of markers in Australian wheat breeding. Aust. J. Agric. Res. 52: 1349-1356.
Eathington, S. R., T. M. Crosbie, M. D. Edwards, R. S. Reiter, and J. K. Bull. 2007. Molecular markers in a commercial breeding program.
Crop Sci. 47(S3):S154-S163.
Habier, D., R. L. Fernando, and J. C. M. Dekkers. 2007. The impact of genetic relationship information on genome-assisted breeding values.
Genetics 177:2389-2397.
Heffner, E. L., M. E. Sorrells, and J-L. Jannick. 2009. Genomic selection for crop improvement. Crop Sci 49: 1-12.
Hospital, F. 2009. Challenges from effective marker-assisted selection in plants. Genetics 136:303-310.
Lande, R., and R. Thompson. 1990. Efficiency of marker-assisted selection in the improvement of quantitative traits. Genetics 124:743-756.
Meuwissen, T. H. E., B. J. Hayes, and M. E. Goddard. 2001. Prediction of total genetic value using genome-wide dense marker maps. Genetics
157: 1819-1829.
Moreau, L., A. Charcosset, F. Hospital, and A. Gallais. 1998. Marker-assisted selection efficiency in populations of finite size. Genetics
148:1353-1365.
Moreau, L., S. Lemarié, A. Charcosset, and A. Gallais. 2000. Economic efficiency of one cycle of marker-assisted selection. Crop Sci.
40:329-337.
Nakaya, A., and S. N. Isobe. 2012. Will genomic selection be a practical method for plant breeding? Annal. Bot. 110. 1303-1316.
Peleman, J. D., and J. R. van der Voort. 2003. Breeding by design. Trend Plant Sci. 8: 330-334.
Piepho, H. P., J. Möhring., A. E. Melchinger, and A. Büchse. BLUP for phenotypic selection in plant breeding and variety testing. Euphytica. 161: 209-228.
Podlich, D. W., C. R. Winkler, and M. Cooper. 2004. Mapping As You Go: An effective approach for marker-assisted selection of complex traits. Crop Sci. 44: 1560-1571.
Reyna, N., and C. H. Sneller. 2001. Evaluation of marker-assisted introgression of yield QTL alleles into adapted soybean. Crop Sci. 41: 1317-1321.
Tanksley, S. D., and C. M. Rick. 1980. Isozymic gene linkage map of the tomato: Applications in genetics and breeding. Theor. Appl. Genet. 57: 161-170.
Utz, H.F., and A.E. Melchinger. 1994. Comparison of different approaches to interval mapping of quantitative trait loci. In: Ooijen, J.W. van, and J. Jansen (eds.), Biometrics in Plant Breeding: Applications of Molecular Markers. Wageningen, 195-204.
Yousef, G. G., and J. A. Juvik. 2001. Comparison of phenotyoic and marker-assisted selection for quantitative traits in sweet cor. Crop Sci. 41: 645-655.
Zhong, Shengqiang, and Jannink, Jean-Luc. 2007. Using QTL results to discriminate among crosses based on their progeny mean and variance. Genetics 177(1): 567-576.
A statistical artefact that is due to the deviation of estimates from true values by random error. In a mapping experiment, the loci that are deemed significant are enriched for those in which the estimated effects benefit from random error that happens to fall in the right direction. Therefore, significant QTLs are disproportionately those in which the effect sizes are inflated by chance.

