4.1 Intervals: Tutorial
Intervals
An interval is the measurement of the distance in pitch between two notes. Intervals can be represented harmonically, when two notes are played simultaneously, or melodically, when two notes are play successively. The method for measuring and naming intervals is the same for both harmonic and melodic intervals.

Naming intervals
There are two parts to any interval name: interval quality and interval size.
Interval size is determined by how far apart the notes letter names are, regardless of what accidentals are involved. We always count interval size starting from the lower pitch up to the higher pitch, regardless of whether the interval is ascending or descending. The starting pitch is always 1. For example, for the notes C# up to G# , we would count C as 1, D as 2, E, as 3, as 4 and G as 5. So, C# up to G# is a 5th in size. When determining size for A descending to E, we count from E as 1 to A as 4 to get a 4th in size.

Interval quality tells us the type of interval being used. The main types of intervals are perfect, major, minor, augmented, and diminished.
- Perfect intervals include unisons, 4ths, 5ths, and octaves
- Major and minor intervals include 2nds, 3rds, 6ths, and 7ths
- Augmented and diminished intervals result from altering a perfect, major, or minor interval.
The number of half steps in each interval determines the quality of the interval. The list below shows the quality of the interval and how many half steps it contains.
- PU = 0
- m2=1
- M2 =2
- m3=3
- M3=4
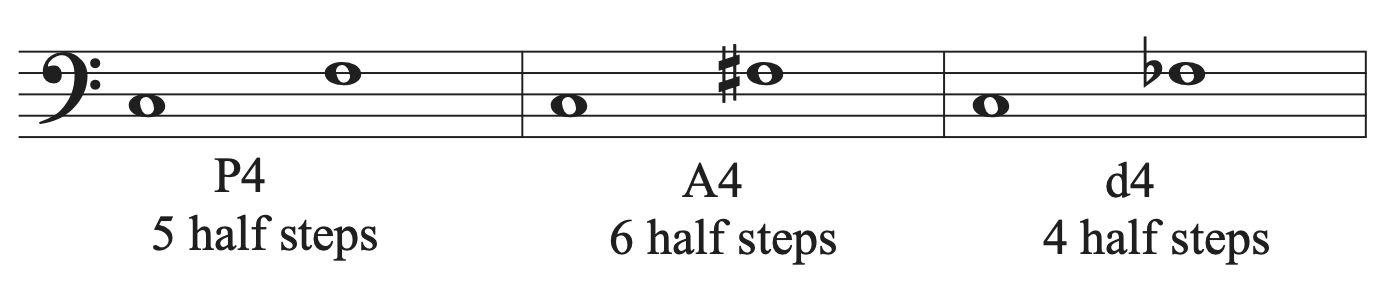
- P4=5
- A4/d5=6 (also known as a tritone, though that is not a specific enough label for naming intervals)
- P5=7
- m6=8
- M6=9
- m7=10
- M7=11
- P8=12
In order to help yourself count half steps, you can draw a keyboard or write out the list of half steps: C C#/Db D D#/Eb E F F#/Gb G G#/Ab A A#/Bb B C
Look at the examples below. Determine the interval size and count the half steps in each interval to determine the quality.

A. Size is a 3rd, has 4 half steps: M3
B. Size is a 6th, has 8 half steps: m6
C. Size is a 2nd, has 1 half step: m2
D. Size is a 5th, has 7 half steps: P5
E. Size is a 4th, has 5 half steps: P4
F. Size is a 7th, has 11 half steps: M7
Augmented and Diminished Intervals
When an extra half step is added or taken away from an interval, it changes the interval quality. Remember that letter names determine interval size, so the interval size will not change when adding or subtracting a half step unless the letter names of the pitches change. Look at the chart below.
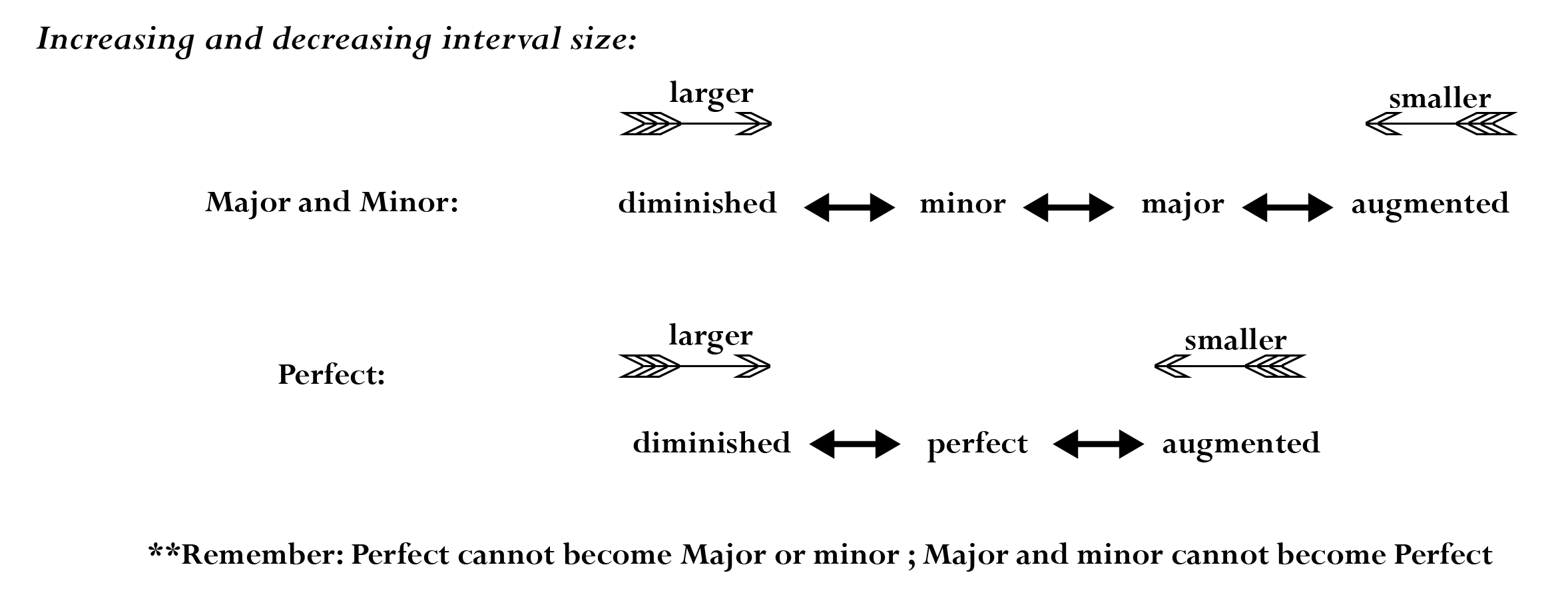
If an interval is perfect and is increased by a half step, it becomes an augmented interval (symbolized by A or +). If it decreases by a half step, it becomes diminished (symbolized by d or by using a degree sign: ˚ ). A perfect interval can never become a major or minor interval.
In an interval is major and it is increased by a half step, it becomes augmented. However, if it decreased by a half step it becomes minor. It has to be decreased by an additional half step in order to become diminished. Major intervals can never become perfect.

If an interval is minor and is decreased by a half step, it becomes diminished. However, if it is increased by a half step it becomes major. It has to be increased by another half step in order to become augmented. Minor intervals can never become perfect.

Doubly augmented and diminished intervals are possible, but rare.


Quickly recognizing intervals
Looking at how the two notes of an interval are placed on the staff can quickly tell you interval size.
- 2nds are always on an adjacent line and space
- 3rds are always a line or a space apart
- 4ths are always a line to a space or a space to a line and look one note larger than a 3rd
- 5ths are always two lined notes separated by one line or two spaced notes separated by a space
- 6ths are always a line to a space or a space to a line and look one note larger than a 5th
- 7ths are always space to space or line to line and look one less than an octave

Know your keys/scales and think of intervals in terms of being in a key
- Major scale (ascending) has only Major and perfect intervals
- Minor scale (natural minor ascending) has M2, m3, P4, P5, m6, m7
- If the bottom note in the interval is “tonic” then you can quickly tell if that interval is in a Major or minor key if you know your key signatures. If it’s not found in a key, you can see how it was altered to create the interval and label it accordingly.
- For example, if you see B to D#, you can think of B as tonic and determine that D# is an expected note in the key. Therefore, the interval will be a M3. If you see A to C, you can think of A as tonic and determine that A Major would have a C#, but a minor has a C natural, so the interval must be a m3.
Be able to recognize intervals by sound. You can play or sing them to aurally check your answers.
If intervals are played harmonically, use your knowledge of consonance and dissonant to help determine the interval. Consonant intervals sound pleasing to the ear and include perfect intervals, 3rds, and 6ths. Dissonant intervals are not pleasing to the ear and include 2nds, 7ths, augmented and diminished intervals.
Enharmonic Equivalence
Just as it is possible to have enharmonically equivalent notes and keys, it is also possible to have intervals that sound the same but are spelled differently. Think of the harmonic minor scale. It has 3 half steps between scale degrees 6 and 7. It is written like an augmented 2nd in the scale, but it sounds the same as a minor 3rd. It’s important to double check the spelling of intervals so that the size of the interval always reflects the distance between the letter name of the two pitches, regardless of accidentals used.

Compound Intervals
Compound intervals are intervals that are larger than an octave. We call intervals that are an octave or less in size simple intervals. When naming compound intervals, the size of the interval is equal to the original interval size plus 7. Quality remains the same as it would be for a simple interval:
- m2 becomes m9
- M2 become M9
- m3 becomes m10
- M3 becomes M10
- P4 becomes P11
- P5 becomes P12
- m6 becomes m13
- M6 becomes M13
- m7 becomes m14
- M7 becomes M14
- P8 becomes P15
Look at the following compound interval examples.

Inverting Intervals
An interval can be inverted by switching the order of the pitches on the staff so that the pitch that was lower is higher, or the pitch that was higher is lower.

When an interval is inverted, it must be named according to its new position, so will have a different name from the original interval. The new interval size can be found by subtracting the original interval size numerical number from 9:
- 2nd inverts to 7th
- 3rd inverts to 6th
- 4th inverts to 5th
- 5th inverts to 4th
- 6th inverts to 3rd
- 7th inverts to 2nd
The quality of the interval also changes when it is inverted, with the exception of perfect intervals:
- minor inverts to major
- major inverts to minor
- perfect stays perfect
- augmented inverts to diminished
- diminished inverts to augmented
Look at the following interval inversions.

How carefully do you look at intervals in the music you are practicing or studying? What is the smallest interval that you see in your music and how is it used? What is the largest and how is it used? Are there any intervals that appear more often than others? Do they appear in specific places in the music? Can you hear the different qualities of the important intervals in your music? How does being able to recognize and hear intervals change the way that you hear the music? Does it make it easier to practice, perform, or teach?

